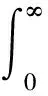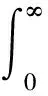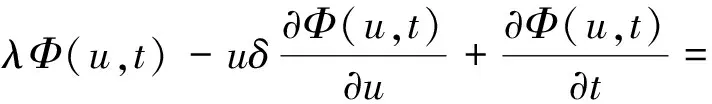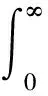常利息力下稀疏风险模型的生存概率
2014-03-27王贵红赵金娥
王贵红,赵金娥
(1.玉溪农业职业技术学院 计算机科学系, 云南 玉溪 653106;2.红河学院 数学学院, 云南 蒙自 661199)
风险理论不仅是当前保险业、精算界研究的重要课题,而且也是数学学科的一个重要分支,其主要研究和处理保险实务中的随机风险模型,并从定量的角度分析保险公司经营的安全性.生存概率作为其中一个核心课题,在风险理论的研究中有着举足轻重的地位[1-2].经典风险模型由瑞典精算师Lundberg[3]于1903年创立,它在理论上为风险模型奠定了重要的思路,但作为一种理论模型由于其在应用上的方便及在数学上的简单性,学者们对它的研究已经比较深入和完善.在经典风险模型中,总是假定保险公司的保费收入是时间的线性函数,但在保险公司的实际运营中,经常要根据以往的索赔经验对保费率进行调整,以致于在未来某个固定的时期内保险公司收到的保险费是随机的.根据这一实际情况,文献[4-7]研究了保费收入是复合Poisson过程的风险模型,并假设保险公司的保单到达过程与索赔计数过程是相互独立的.事实上,由于保险公司所卖出的保单数越多,其发生的索赔次数也应更多,因此保险公司的索赔计数过程与保单到达过程之间应具有某种相依性.此外,现实生活中,货币利息强度总是存在且对保险公司的经营也有一定的影响,因此研究常利息力下稀疏风险模型的生存概率是非常有现实意义的.基于以上事实,考虑一类常利息力下的风险模型,其中保单到达过程为复合Poisson过程,而索赔的计数过程为保单到达过程的p-稀疏过程.利用盈余过程的马氏性及概率论、随机过程等学科的理论方法,得到了模型在有限时间内和无限时间内生存概率满足的积分-微分方程,并在保费额及索赔额均服从指数分布时得到了有限时间内生存概率的微分方程.
1 模型引入
定义1 设(Ω,F,P)是一包含本文所有随机变量(随机过程)的完备概率空间,则对u≥0,t≥0,定义保险公司在t时刻的盈余为:
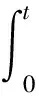
(1)
其中:
1)δ≥0为常利息力,常数u表示保险公司的初始准备金;
2) {M(t),t≥0}是参数为λ>0的Poisson过程,表示保险公司在(0,t]时间内收到的保单数;
3) {Yk,k≥1}是一独立同分布的非负随机变量序列,表示保险公司第k次收取的保险费,其分布函数为G(y);
4) {N(t),t≥0}是{M(t),t≥0}的一个p-稀疏过程,即{N(t),t≥0}是强度为λp(0 5) {Xk,k≥1}是一独立同分布的非负随机变量序列,表示保险公司第k次的索赔额,其分布函数为F(x); 6) {Xk,k≥1},{Yk,k≥1}和{M(t),t≥0}相互独立. 定义2 记T=inf{t≥0,Uδ(t)<0},表示保险公司的破产时刻,则在初始准备金为u的条件下,分别定义保险公司的最终破产概率及在t时刻之前的破产概率为 ψ(u)=P{T<∞|Uδ(0)=u},ψ(u,t)=P{T 对应的生存概率为Φ(u)=1-ψ(u),Φ(u,t)=1-ψ(u,t). 定理1 风险模型(1)在无限时间内的生存概率Φ(u)满足以下积分-微分方程: (2) 并满足边界条件: Φ(+∞)=1,Φ(0)=0, 证明令h(t)=ueδt-u,则在很小的时间区间(0,Δt)内,由全概率公式及盈余过程的马氏性,有 等价地 上式两边同时除以Δt,并令Δt→0,则有 即 由此可得 由文献[5]知Φ(+∞)=1,显然Φ(0)=0,在(2)式中令u→0,得 推论1 若F(x)=1-αe-αx(x≥0),G(y)=1-βe-βy(y≥0),则对于任何u≥0,Φ(u)满足下面的微分方程: uδΦ‴(u)+[2δ-λ-uδ(β-α)]Φ″(u)+[(λ-δ)(β-α)-uδαβ]Φ′(u)=0. 并满足边界条件 Φ(+∞)=1,Φ(0)=0, 证明将F(x)=1-αe-αx,G(y)=1-βe-βy代入(2)式,有 (3) 由文献[8]知Φ(u)具有可微性,故对(3)式两边关于u求导,得 (4) (4)式两边再对u求导,有 (5) 由(3)~(5)式,即得 uδΦ‴(u)+[2δ-λ-uδ(β-α)]Φ″(u)+[(λ-δ)(β-α)-uδαβ]Φ′(u)=0 定理2 风险模型(1)在有限时间内的生存概率Φ(u,t)满足下列偏微分-积分方程: 并满足边界条件: Φ(+∞,t)=1,Φ(u,∞)=Φ(u). 证明类似于定义1,有 Φ(u,t)=[1-λΔt+o(Δt)]Φ(u+h(Δt),t-Δt)+ 等价地 上式两边同时除以Δt,并让Δt→0,则有 即 参考文献: [1] 龚日朝.广义复合Poisson模型下有限时间内的生存概率[J].数学季刊,2003,18(2):134-139. [2] 王后春.两个风险模型的生存概率的积分方程[J].哈尔滨理工大学学报,2005,10(5):112-114. [3] LUNDBERG F I. Approximerad framstallning af sannolikhetsfunktionen: II. Aterforsakring af kollektivrisker[M].Uppsala.,1903. [4] 赵金娥,王贵红,龙瑶.理赔次数为复合Poisson-Geometric过程的风险模型[J].西南大学学报:自然科学版,2013,35(3):78-83. [5] 方世祖,罗建华.双复合Poisson风险模型[J].纯粹数学与应用数学,2006,22(2):271-278. [6] BOIKOV A V. The Cramer-Lundberg model with stochastic premium process[J]. Theory of Probability & Its Applications, 2003, 47(3): 489-493. [7] 赵金娥,何树红,王贵红.带线性红利和干扰的双复合Poisson风险模型[J].云南民族大学学报:自然科学版,2010,19(1):24-27. [8] 张春生,吴荣.关于破产概率函数的可微性的注[J].应用概率统计,2001,17(3):267-275.2 主要结果