非线性耦合薛定谔方程组的整体吸引子

赵 强,程秀华,霍叶珂

(云南民族大学 数学与计算机科学学院,云南 昆明 650031)

非线性耦合Schrödinger方程组在数学和物理学研究中应用非常广泛. 在光纤通信系统中, 这样的方程通常用来描述非线性情况下光脉冲沿着正交极化轴传播. Menyuk[1]利用该类方程对双折射光纤传播进行了研究.Ismail[2]用Galerkin 方法对该类方程数值解进行了分析. 含有弱阻尼和外力项的非线性Schrödinger方程在文献[3-4]中也有介绍. 吸引子是无穷维动力系统主要研究对象之一, 尤其在20世纪90年代之后，国内郭柏灵、戴正德等[5-9]极大地丰富了关于无穷维动力系统吸引子的研究. 本文讨论的非线性耦合Schrödinger方程组是对文献[2]的改进：

iut-(β+iα)Δu+(|u|2+|v|2)u+iru=f，

(1)

ivt-(β+iα)Δv+(|u|2+|v|2)v+iσv=g.

(2)

其中阻尼系数r,σ>0,常数α,β>0,f(x)和g(x)是与时间无关的外力项, 且f,g∈L2(Ω)×L2(Ω),Ω是R2中的有界开集. 现将方程(1)和(2)改写成

iUt-(β+iα)ΔU+GU+iQU=F,

(3)

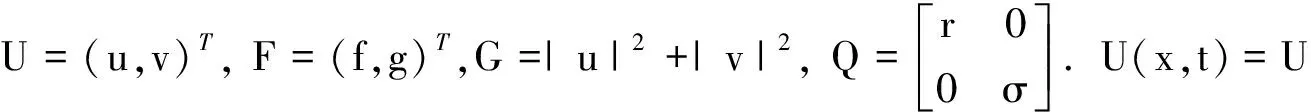
U0=U(x,0);U(x,t)=0,x∈∂Ω.

本文讨论的非线性耦合Schrödinger方程组在空间L2(Ω)×L2(Ω)中整体吸引子的存在性, 并对它的动力行为进行描述.

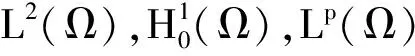
1 解的先验估计

引理1 设U0∈H,F∈H, 问题(3)的解U满足

(4)

(5)

设λ=min{r,σ},r,σ>0, 从(5)得

(6)

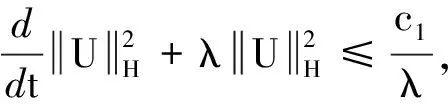
(7)

引理2 设U0∈V,F∈V, 问题(3)的解U满足

(8)

(9)

利用Sobolev嵌入定理和插值定理, 且Ω∈R2, 根据Gagliardo-Nirenberg不等式, 存在常数c, 使得

(10)

(11)

(12)

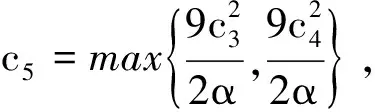
(13)

定理1 设U0∈V∩H,F∈H∩V, 则存在唯一的解U(x,t)=U满足(3), 并且

U∈L∞(0,T;V∩H).

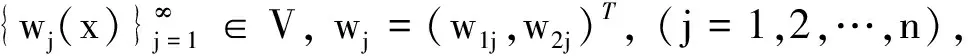
i(Umt,wj)-(β+iα)(ΔUm,wj)+(GUm,wj)+i(QUm,wj)=(F,wj),

(14)

Um(x,0)=U0m(x).

(15)

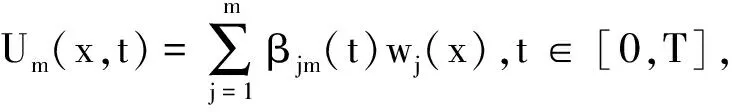
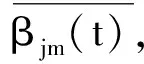
2)唯一性证明. 设U1,U2分别为满足定理1的条件的2个解, 令W=U1-U2, 则

iWt-(β+iα)ΔW+GW+iQW=0.

(16)

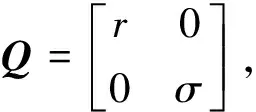
2 整体吸引子

由定理1证明了问题(3)解的存在唯一性可知解对初值是连续依赖的, 若在空间H中定义一个非线性半群S(t):H→H,并满足S(μ+η)=S(μ)+S(η),∀μ,η≥0,S(0)=I;令S(t)U0=U(t), 则S(t)：U0→U(t)定义了空间H上的一个动力系统.

当t≥t0=t0(B,B0), 成立S(t)B⊂B0. 从t到t+τ(τ>0)积分(6)得

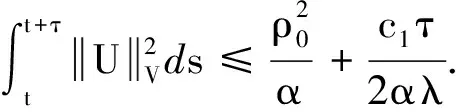
又由引理2证明中得到式子(13), 利用一致Gronwall引理, 设

参考文献:

[1] MENYUK C R. Nonlinear pulse propagation in birefringence optical fiber[J].IEEE J Quantum Electron, 1987, 23:174-176.

[2] ISMAIL M S. Numerical solution of coupled nonlinear Schrödinger equation by Galerkin method[J]. Mathematics and Computers in Simulation, 2008, 78(4): 532-547.

[3] TEMAM R. Infinite dimensonal dynamical systems in mechanics and physics[M]. Springer,1997.

[4] GOUBET O, MOLINET L. Global attractor for weakly damped nonlinear Schrödinger equations inL2(R)[J]. Nonlinear Analysis: Theory, Methods and Applications, 2009, 71(1): 317-320.

[5] GUO Bo-ling, SU Feng-qiu. The global attractors for the periodic initial value problem of generalized kuramato-sivashinsky type equations in multi-dimensions[J].J Partial Diff Eqs, 1993, 6:217-236.

[6] LIONS J L.非线性边值问题的一些解法[M]. 郭柏灵, 汪礼礽,译.广州：中山大学出版社,1992.

[7] 郭柏灵. 非线性演化方程 [M]. 上海:上海科技教育出版社,1998.

[8] 杨干山, 戴正德, 一类蜕化Kuramoto-Sivashinsky方程的整体吸引子[J].数学研究,1996,1 (29):52-62.

[9] 冯廷福，杨慧.一类光学中的非线性Schrödinger方程整体解的存在性[J].云南师范大学学报：自然科学版，2012,32(4):32-36.