多电平逆变器空间矢量控制算法的研究
2014-03-27罗方利韩如成
罗方利,韩如成,李 宁
(太原科技大学 电子信息工程学院,山西 太原 030024)
在高压大功率应用场合,多电平逆变器得到了越来越广泛的应用[1-2].调制技术是多电平变流器的关键性技术之一,其中空间矢量调制技术(SVPWM)在三相系统中得到了广泛应用[3-4].传统的空间矢量调制算法矢量定位规则复杂,计算矢量作用时间要涉及到大量三角函数运算,算法的实时性差,不宜直接向电平数大于3的逆变器中推广.文献[5-6]提出了60°坐标系法,文献[7]提出了45°坐标系法,这些方法都有效避免了大量三角函数的运算,简化了矢量扇区定位和矢量作用时间的计算.但是没有对选取合成矢量和确定开关电压组合作简化研究.文献[8]指出SVPWM算法随着电平数的提高,冗余矢量和开关电压组合数分别以二次方、三次方形式增长,因此选取合成矢量确定开关电压组合仍是一个复杂的过程.
针对上述问题,本文在60°坐标系SVPWM基础上提出一种简化算法.该算法结合开关频率优化原则,给出在(0,π/3)范围内,参考电压对应矢量扫过的各个小三角形扇区对应的合成矢量和开关电压组合计算方法,并通过交替相序和取反运算获取整个电压周期内各个小三角形扇区的合成矢量和开关电压组合.
1 五电平逆变器的主电路结构
多电平逆变器主电路结构主要分为3类[9]:二极管箝位型多电平逆变器、电容型多电平逆变器、级联型多电平逆变器.其中,级联型多电平逆变器采用独立电源供电,可靠性高,不存在直流侧母线电容电压波动问题,因而备受关注.其主电路结构如图1所示.

逆变器A相工作的5个状态输出的相电压分别为-2E,-E,0,E,2E,用SA=-2,-1,0,1,2来表述.同理,B相,C相分别用SB,SC表示.此时,三相级联型五电平逆变器的工作状态可表示为三维向量(SA,SB,SC),该电路共有53=125个工作状态.
五电平逆变器输出的三相电压只能在{±E,±2E,0}中取值.用向量(α,β)表示矢量V.
(1)
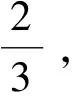
2 60°坐标系SVPWM控制算法原理
2.1 60°坐标系的建立
以图2中α轴为g轴,以与α轴成60°的轴线为h轴,建立新的坐标系,即60°坐标系.并将g轴和h轴同时轴向拉伸1.5倍. 坐标点(α0,β0)在新坐标系下的坐标值为(g0,h0).
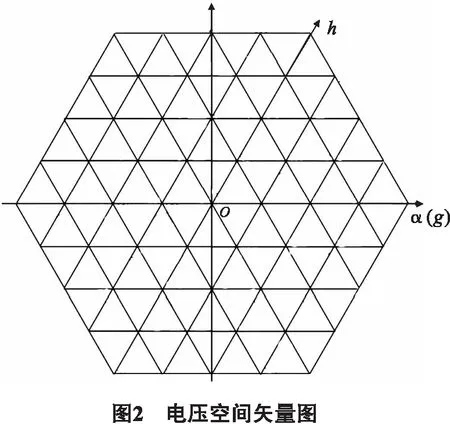
(2)
60°坐标系下的三相电压空间矢量坐标(g,h)为
(3)
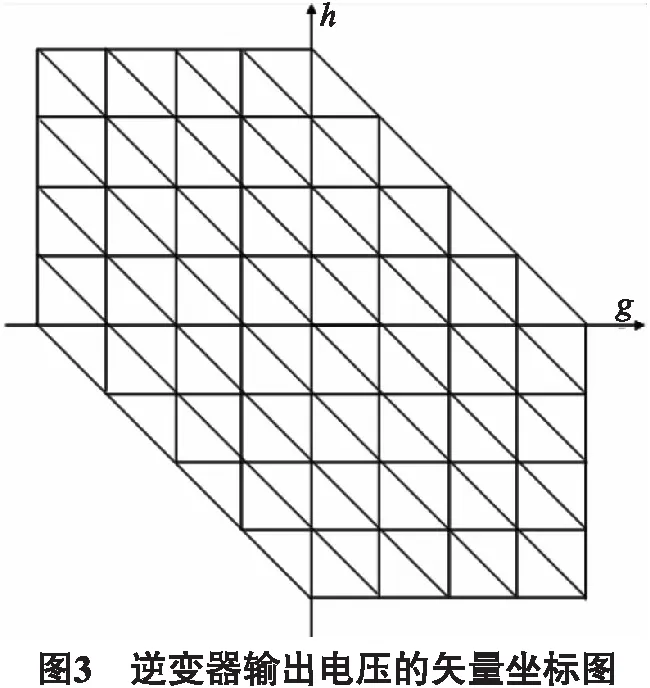
五电平逆变器基本电压矢量如图3所示.
2.2 60°坐标系SVPWM控制算法
2.2.1 参考电压矢量的定位
如图4所示,点(gN,hN)为参考电压矢量的坐标值.则A点坐标:(gA,hA)=([gN],[hN]);B点坐标: (gB,hB)=([gN],[hN]+1);C点坐标:(gC,hC)=([gN]+1,[hN]+1);D点坐标: (gD,hD)=([gN]+1,[hN]).
通过A、B、C、D点的坐标,可以判断参考电压矢量落在哪个小正方形中.如果gN+hN≤gB+hB,则参考矢量落在下三角形,即图4中区域II,否则参考矢量在上三角形,即图4中区域I.
2.2.2 合成矢量及其作用时间的确定
如图4中所示,如果参考电压矢量落在下三角形,即区域II,则合成矢量VOA,VOB,VOD及其作用时间的关系由下式确定[10]:
TOA·VOA+TOB·VOB+TOC·VOC=Vr·Ts;
TOA+TOB+TOC=Ts.
(4)
将图4中的矢量坐标值代入式(4)得:

TOA=Ts·(1-|gN-gA|-|hN-hA|);TOB=Ts·|hN-hA|;TOD=Ts·|gN-gA|.
(5)
如果参考电压矢量落在上三角形,则合成矢量VOC,VOB,VOD及其作用时间分别为:
TOC=Ts·(1-|gN-gC|-|hN-hC|);
TOD=Ts·|hN-hC|;
TOB=Ts·|gN-gC|.
(6)
2.2.3 开关状态的计算
逆变器开关状态的确定主要有2种方法.第1种方法就是软件在线计算方法.矢量对应的开关状态由下式确定[11]:
(7)
第2种方法就是查表的方法.先人工确定图2或图3中每个矢量对应的开关状态,将其存储在控制器内存中,然后让软件通过读取内存的方式获取开关矢量对应的开关状态.
3 开关状态计算方法的优化
3.1 2种传统方法存在的问题
第1种方法原理简单,内存占用率低,但是不能应用五段式和七段式调制方法,多解取舍逻辑复杂,软件难以实现.第2种方法要占据大量内存,但是对于电平数为N的逆变器而言,需6N3个地址空间.这些数据都要事先通过人工计算好,工作量大.
3.2 优化的开关状态的计算方法
优化的基本思路就是充分利用三相正弦波电压的周期性和对称性,求出一部分的扇区的开关状态,进而推导出其他所有扇区的开关状态.如图5所示,将1个周期的电压等分成6段,分别记为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ.当确定了第I段范围内的电压波形后,可通过交替相序的方法得到整个周期的电压波形.例如:第II段范围内,A相的幅值等于B相在第Ⅰ段(0,π/3)范围内的幅值乘以-1,B相的幅值等于C相在第Ⅰ段范围内的幅值乘以-1,C相的幅值等于A相在第Ⅰ段范围内的幅值乘以-1.
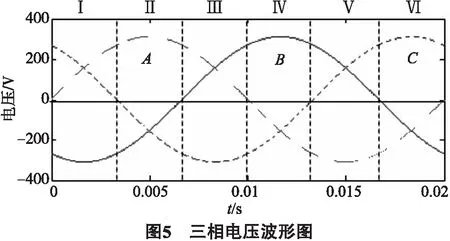
按照上述规律,只需求解逆变器第Ⅰ段范围内各开关矢量的开关状态,通过相序交替和取反运算,就能获得参考电压周期内所有的开关状态.
假设逆变器在第Ⅰ段某个相位点的开关状态为(SA0,SB0,SC0),则第i段相对应的开关状态(SA,SB,SC0)为:
当i=Ⅰ时, {SA,SB,SC0}={SA0,SB0,SC0};
当i=Ⅱ时,{SA,SB,SC}={-SB0,-SC0,-SA0};
当i=Ⅲ时,{SA,SB,SC}={SC0,SA0,SB0};
当i=Ⅳ时,{SA,SB,SC}={-SA0,-SB0,-SC0};
当i=Ⅴ时,{SA,SB,SC}={SB0,SC0,SA0};
当i=Ⅵ时,{SA,SB,SC}={-SC0,-SA0,-SB0}.
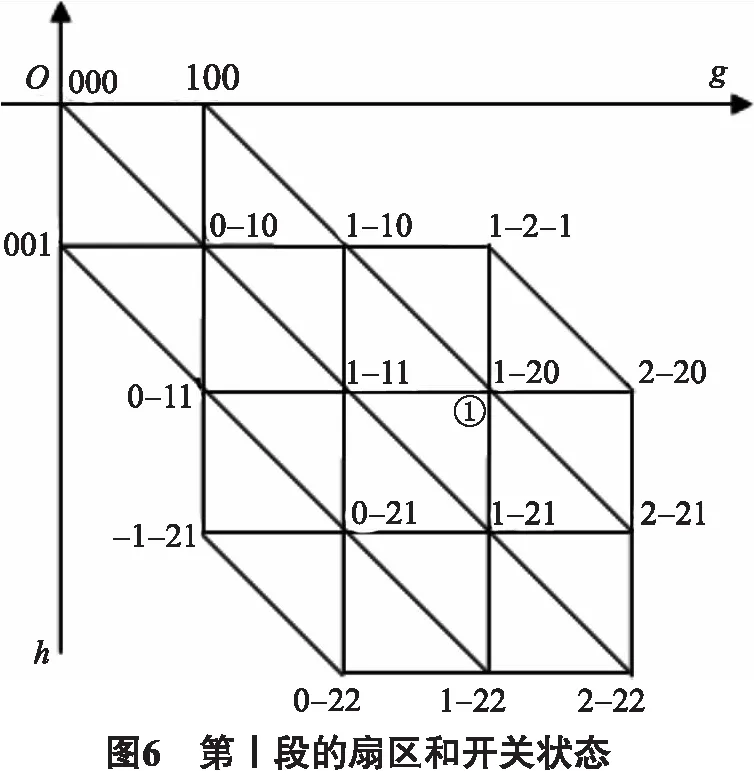
本文称上述方法为相序交替归一化方法.在第I段(0,π/3)内,参考电压扫过的扇区及扇区对应的开关矢量和开关状态如图6所示.
图6中,选取开关状态的原则:① 每个小三角形扇区能够找到一个遍历它的3个顶点的方式使得从上一个顶点切换到下一个顶点时,开关状态的3个坐标值只有1个发生改变,且该变量为1;②B相的开关状态与自己关于OM对称,A相的开关状态与C相关于OM对称.
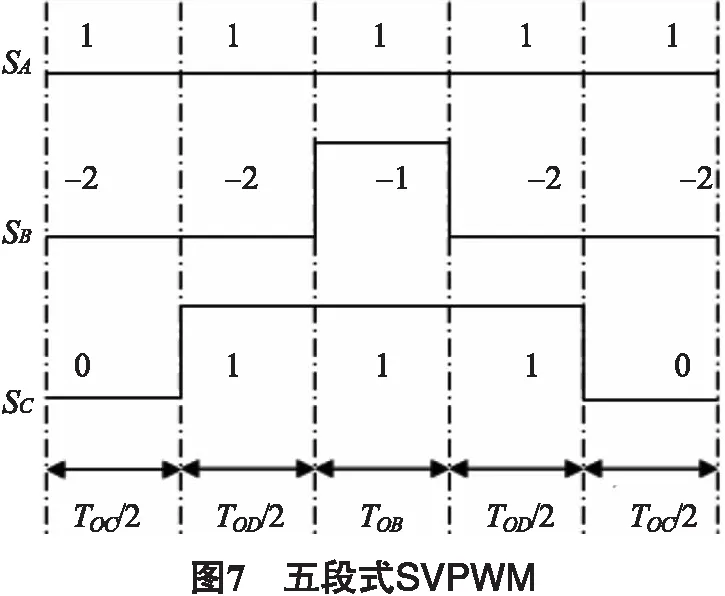
计算出开关状态后,本文采用五段式SVPWM方法产生PWM波形.以图6中①标示的三角形扇区为例.开关状态切换顺序为(1,-2,0)→(1,-2,1)→(1,-1,1)→(1,-2,1)→(1,-2,0),PWM波形和各个状态作用时间如图7所示.
4 仿真研究
在Matlab/Simulink仿真环境下建立模型、仿真.仿真参数为:E=150 V,参考电压频率f=50Hz,调制度m=0.99,负载R=5 Ω,L=1 mH,采样频率10 kHz.
仿真结果如图8所示.逆变器输出的相电压是5电平的阶梯波,负载的相电压是17电平的阶梯波,十分接近正弦波.150次以下各次谐波总畸变率THD=0.20%,谐波分量小.
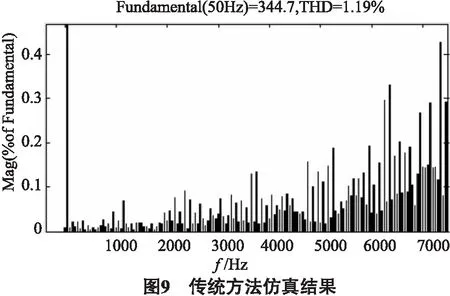
采用传统的开关状态计算方法.负载相电压谐波频谱如图9所示.比较图8(d)和图9,可知采用相序交替归一化法的负载相电压中150次以下的谐波总畸变率远小于不采用相序交替归一化方法的畸变率.上述实验结果表明,相序交替归一化方法在改善输出波形性能方面具有明显的作用.

5 结语
本文在具体分析了60°坐标系SVPWM算法的基础上,对60°坐标系SVPWM算法进行了一些优化工作.在计算开关状态时,提出了相序交替归一化的方法.该方法不仅有效减小了软件设计时计算开关状态的工作量,降低了开关状态数据对内存的占用率,而且还在抑制负载电压谐波上具有显著的作用.

参考文献:
[1] SEO J H, CHOI C H, HYUN D S. A new simplified space-vector PWM method for three-level inverters[J].Power Electronics, IEEE Transactions on, 2001, 16(4): 545-550.
[2] 胡磊,何湘宁,邓焰.多电平逆变器空间矢量脉宽调制的简化算法[J].电力电子技术,2005,39(5):12-14.
[3] 姜旭,肖湘宁,赵洋,等.改进的多电平SVPWM及其广义算法研究[J].中国机电工程学报,2007,27(4): 90-94.
[4] BUSQUETS-MONGE S, BORDONAU J, BOROYEVICH D, et al. The nearest three virtual space vector PWM-a modulation for the comprehensive neutral-point balancing in the three-level NPC inverter[J].Power Electronics Letters, IEEE, 2004, 2(1): 11-15.
[5] 赵辉,李瑞,王红君,等.60°坐标下三电平逆变器SVPWM方法的研究[J].中国机电工程学报,2008,28(24):39-45.
[6] SUN L, ZHUO F, XIONG L. A fast multi-level space vector PWM method based on sequence cyclic shift[C]//Industrial Electronics (ISIE), 2012 IEEE International Symposium on. IEEE, 2012: 40-45.
[7] 朱思国,欧阳红林,晏建玲,等. 45°坐标下三级联逆变器简化空间矢量调制及性能优化研究[J].电工技术学报,2012,27(2):68-76.
[8] 刘铮.多电平逆变器空间矢量控制技术研究[D].长沙:湖南大学,2008.
[9] 刘凤君.多电平逆变技术及其应用[M].北京:机械工业出版社,2007.
[10] 张卫峰,余岳辉,刘璐.三电平逆变器空间电压矢量控制算法仿真研究[J].电力电子技术,2006,41 (1):1-5.
[11] 于月森,赵成成,符晓,等.基于g-h坐标系的SVPWM控制算法5电平逆变器仿真研究[J].电气传动,2011,41(21): 37-40.
