一款广义范德蒙行列式的值*

黎罗罗

(中山大学新华学院，广东 广州 510520)

相当多的理论与应用问题中出现形式各异的广义范德蒙(Vandermonde)矩阵及其行列式[1-3]。

组合数学方法在讨论线性常系数齐次递推关系“初值问题”解的存在与唯一性时，具有理论支撑意义的也是一款广义范德蒙矩阵的行列式。设b1,b2,…,bk为给定数且bk≠0，则递推关系

an+b1an-1+…+bkan-k=0(n≥k)

的通解为

(1)

其中λi为递推关系的特征多项式的mi重根。Qi(n)是n的不超过mi-1次的多项式。当给定dt(t=0,1,…,k-1)按at=dt(t=0,1,…,k-1)确定满足“初值”的特解时，出现关于lij的线性方程组，文[3][4]详细地给出了该方程组系数矩阵A的结构。A为k×k分块矩阵

A=[A1,A2,…,As]

其中Ai为k×mi阶子块：

(2)

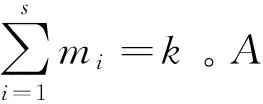
文[3-5]等不加证明地采用如下公式描述其行列式的值

(3)

文[6]在给出如(1)所示的通解表达式后，指出关于lij的线性方程组的矩阵的行列式的值为

(4)

用简单的例子即不难验证这两个表达式都是错误的。由式(1)导致式(4)的说法至少可上溯到上世纪70年代[7]，而在至今期间出版的教科书中沿用[6,8]。实在有订正的必要。

由于这些结论不加证明也没有给出出处，本文先以如下定理给出上述广义范德蒙行列式detA的正确的值，然后对教材编写提出修改的建议。

定理1 设广义范德蒙矩阵A=[A1,A2,…,As]如上，则

(5)

注2 ①若存在i≠j使得λi=λj，则式(5)已经成立；②若某mi>1而λi=0，式(5)也已经成立。两种情况下行列式的值为零。否则按式(5)，行列式值不为零。下面的讨论中，均假定这两种情况不发生。

证明对范德蒙子块的个数s作数学归纳法。

s=1时，m1=k，

A=

容易计得

(最后一步用经典范德蒙行列式的结论)，也就是

可见定理结论在范德蒙子块数s=1时成立。

归纳假设：定理结论在矩阵含s-1个范德蒙子块时成立，由上面的约定，其值不为零。

今有k阶广义范德蒙矩阵含s个范德蒙子块，记为A[s]。满足注2中的约定。

先设ms>1。视detA[s]为λs的多项式，则由行列式基本性质知λ1,λ2,…,λs-1及0均为该多项式的根。于是

(6)

其中μj与βj(j=1,2,…,r)是该多项式可能有的、异于λ1,λ2,…,λs-1及0的根及其重数。

观察detA[s]的结构。依其最后ms列作拉普拉斯展开，即知上述λs之多项式的最高次数为

(k-1)+(k-2)+…+(k-ms)=

(7)

λs的这一幂次由A[s]右下角的ms阶子式提供，注意该子式的余子式恰是一个含s-1个子块的广义范德蒙行列式(其矩阵记之为A[s-1])，由归纳假设，它不为零。因此，λs最高次项的系数为

Ks=detA[s-1]×

detA[s-1](ms-1)!(ms-2)!…2!

(8)

(最后一式由古典范德蒙行列式的结论得)。另外，据式(6)及式(7)，幂次数的关系为

(9)

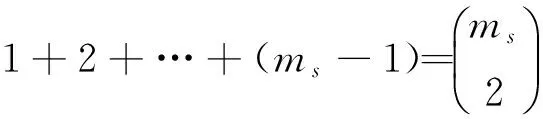
也就是

(10)

现计算诸αi(i=1,2,…,s-1)。先视detA[s]为λ1的多项式，按其前m1列作拉普拉斯展开，知λ1的最高次项由A[s]左下角的m1阶子式

与其代数余子式提供。该代数余子式非零(因为它是含s-1个子块的广义范德蒙行列式，或至多差一个正负号)。同时注意上式中λ1的因子全提出后余下的数字行列式不等于零(经典范德蒙行列式结论)，因此该λ1的多项式的最高幂次数为

(k-m1)+(k-m1+1)+…+(k-1)=

(11)

另一方面，由式(6)、式(8)及归纳假设，λ1的次数为

(12)

式(11)应与式(12)相等，故知

α1=m1ms

(13)

完全类似地可以获得

αi=mims(i=2,3,…,s-1)

(14)

将式(13)与式(14)代入式(9)知

最后，由式(6)，式(8)及归纳假设得

即式(5)成立。

最后，ms=1 情形的证明类似。为节约篇幅，略去。由归纳法原理，定理被证明普遍成立。

小 结

1)式(5)才是A的行列式值。

2)如果将an的通解式改写为

(15)

Bi=

(16)

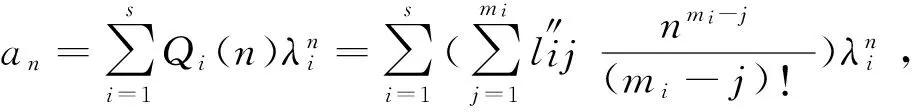
[1] LORING W TU.A partial order on partitions and the genernalized Vandermonde determinant [J]. Journal of Algebra, 2004, 278: 127-133.

[2] 葛谓高,李翠哲,王宏洲. 常微分方程与边值问题[M]. 北京:科学出版社, 2008:195-196.

[3] 潘永亮,徐俊明. 组合数学[M]. 北京:科学出版社,2006: 12-13.

[4] 胡端平,鲁晓成. 组合数学[M]. 武汉: 武汉大学出版社, 2001:239-240.

[5] 孙世新,张先迪. 组合原理及其应用[M]. 国防工业出版社, 2006:149-150.

[6] 许胤龙,孙淑玲. 组合数学引论 [M]. 2版.合肥:中国科技大学出版社, 2011:149-150.

[7] BRUALDI R A. Introductory Combinatorics [M]. Elsevier North-Holland,1977:104-105.

[8] 王天民. 组合数学教程[M]. 北京: 机械工业出版社, 1990: 103-104.