基于 Hadgem2_ES的气候变化对金华江流域枯水变化的影响评估*

高希超，马 冲，朱冠天，朱 仟，许月萍

(1.浙江大学建筑工程学院水文水资源研究所， 浙江杭州 310058; 2.浙江省水文局，浙江杭州 310009)

1 背景介绍

21世纪以来，气候变化引发的极端水文事件如洪涝灾害、干旱等有愈来愈严重的趋势，已引起政府、学者及民众的广泛关注[1]。国内外专家、学者对气候变化对水文水资源的影响评估作出了比较详实的论述。张建云[2]从防洪安全、供水安全、水生态环境安全和水工程安全四个方面阐述了气候变化对中国水安全的可能影响。王国庆等[3]采用流域水文模拟方法分析评估了气候变化和人类活动对径流量的影响。Richard等[4]评估了最新一代的气候情景模式，为后续气候变化的研究提供了新的思路并奠定了理论基础。然而关于气候变化对枯水径流的影响研究特别是在历史降雨比较充分地区的文章却鲜有发表。近年来浙江省几乎每年都会出现旱情，枯水季水资源严重缺乏，部分地区甚至出现用水危机。因此气候变化对枯水径流的影响同样应该引起重视。

对于不同的研究方向，枯水径流有着不同的含义。在某些研究中，枯水径流被认为是每年旱季中河流的实际径流，也有研究把重点放在两次枯水间隔出现的时间和环境，或者其对整个河滨生态环境的影响[5]。WMO (世界气象组织)曾经把枯水径流定义为超长干旱天气中河流中的径流，但Smakhtin[5]认为，枯水径流是一种季节性的现象，是整个径流体系中不可分割的一部分，从而把它与干旱区分开来。

研究选取了钱塘江流域的子流域金华江流域作为研究区域，以1975-2004年作为基准期，2071-2100年为预测期，使用多站统计降尺度工具GIST来模拟未来的降雨和温度，再使用集总式水文模型GR4J来模拟金华江流域的径流，并利用枯水指数7Q10和30Q10来分析气候变化对金华江流域枯水的影响。

2 研究方法

2.1 数据来源

是钱塘江流域的一部分，位于北纬28.25°-29.75°，东经119.25°-120.75°之间。流域中五个水文站金华、武义、义乌、东阳和永康有长系列实测数据。金华江流域总面积约5 996 km2，基准期年均降雨量在1 600 mm左右，降雨多集中在5-7月。流域属于亚热带季风气候，夏季高温多雨，冬季干燥寒冷。流域全年平均温度17.5 ℃，最高温度超过40 ℃，最低温度低于0 ℃[6]。流域的主要河流金华江是钱塘江的支流之一，发源于磐安县龙乌尖，汇于衢江。河流全长达到195 km，河流比降为3%。

本文的研究数据分为2个部分:① 金华江流域基准期的实测日数据，包括降雨、径流、最高温度和最低温度。② CMIP5中Hadgem2_ES模型的全球气候模式模拟结果，数据包括降雨、最高温度和最低温度的月均值。CMIP5 数据包含了4个典型浓度路径情景，即RCP2.6，RCP4.5, RCP6.0以及RCP8.5。RCP2.6情景假定全球平均温度上升被限制在2.0 ℃之内，其中21世纪后半叶能源应用为负排放。辐射强迫在2100年之前达到峰值3 W/m2，到2100年下降至2.6 W/m2。二氧化碳浓度在达到峰值49 μg/g 后下降。RCP4.5情景中，2100年时辐射强迫稳定在4.5 W/m2，二氧化碳浓度稳定在65 μg/g 。RCP6.0情景表示在2100年之后，辐射强迫稳定在6 W/m2，二氧化碳浓度稳定在85 μg/g 。RCP8.5情景下，2100年的辐射强迫达到8.56 W/m2，且上升不会停止，二氧化碳浓度达到137 μg/g[7]。

2.2 GIST模型

GIST是由美国佛罗里达大学的Baigorria等[8]开发的多站统计降尺度工具。在本文中，GIST用于计算预测期的降雨与温度。与传统的统计降尺度工具不同，GIST考虑了不同站点降雨量之间的空间相关性。相关系数ρij被用来表示各站点之间降雨的相关系。ρij的计算公式为[8]：

(1)

式中，η是降雨时间序列的长度，χi和χj是不同站点某一天的降雨量，μi和μj不同站点的降雨均值，σi和σj则是方差。

降雨的产生分为两个阶段，第一阶段是计算降雨事件是否发生，第二阶段是计算其降雨量。降雨事件是否发生通过初始边界条件和率定的参数，以及后续的重取样和二阶马尔科夫链确定。降雨事件确定后，再通过式(2)确定降雨量。

(2)

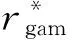
GIST基本输入包括历史的降雨和最高最低温的时间序列和Change Factor[9]，输出是未来的降雨和最高最低温度。计算结果表明，GIST能很好模拟流域的未来降雨，并能较好的保留不同水文站降雨的空间相关性。目前，各种天气发生器都能较好的模拟温度。同样，GIST温度模拟的准确性非常高，这里不再描述。

2.3 水文模型GR4J

GR4J模型是一个概念性水文模型，被广泛用于水文模拟[10]。

GR4J共有4个参数，分别为蓄水容量X1，地下水交换系数X2，前一天的地下水容量X3，水文过程线的时间基准X4。其主要输入是降雨，径流和潜蒸发。率定过程中，以Nash效率系数为主要目标函数来判断率定效果的好坏。GR4J的模型结构如图1所示[11]。图中Pn净雨量，Es为实际蒸散发量，Perc为下渗水，UH1和UH2为控制过程单位线，Q为最终的径流。

在该模型中，未来的降雨由GIST模型模拟所得，潜蒸发则由HARGREAVES法计算而得[12]。计算公式如公式(3)下所示。公式中，其中Ra为日辐射量，单位为mm/d ，Tmax、Tmin分别最日最大温度和日最小温度，单位为℃。C取0.0023，E取0.5，T取17.8。

ETH=C·Ra·(Tmax-Tmin)E·

(3)

图1 GR4J模型结构图Fig.1 Model structure of GR4J model

3 结 果

3.1 GIST计算结果

在本文中，GIST用来模拟未来的降雨量和温度。选取1975-2004年为模拟的基准期。基准期的历史数据用于率定GIST的参数。由于作为多站统计降尺度方法，模拟和实测的相关系数被用来评估GIST模拟的效果。比较结果见图2。这里，历史数据和基准期内模拟值的月均值比较采用了由泰森多边形计算的面雨量和平均温度比较，结果如图3和4所示。

图2 基准期金华江流域各站点降雨量实测值与模拟值相关系数比较Fig.2 Pearson’s correlations of daily precipitation in baseline period

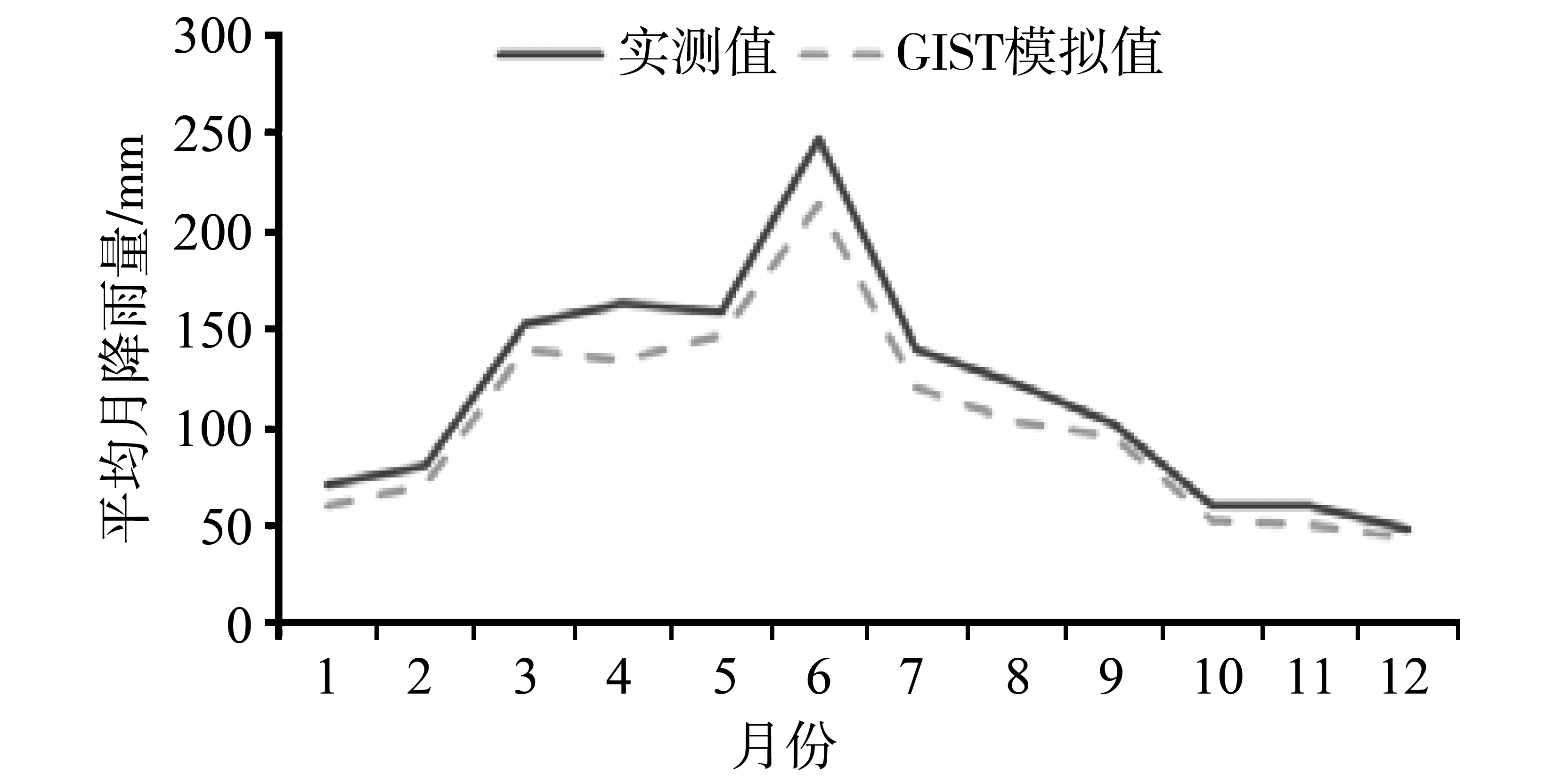
图3 基准期金华江流域实测月面雨量与模拟月面雨量比较Fig.3 Comparison of the daily precipitation of the Jinhua River Basin in baseline period

图4 基准期金华江流域实测温度月均值与模拟温度月均值比较Fig.4 Comparison of the daily temperature of the Jinhua River Basin in baseline period

从图中可以看出，金华江流域的5个水文站降雨量具有较高的空间相关性，而GIST的模拟结果较好的保留了这些空间相关性。从降雨量的月均值来看，尽管模拟值相对于实测值略有偏小，但接近实测值。而变化趋势则和实测值完全一致。从图中可以看出，温度的模拟值和实测值几乎完全重叠。这表明，GIST能很好地完成降雨和温度的模拟，这些值用于下一步径流的模拟工作。

3.2 GR4J率定结果

选取1975-1984年10 a的径流历史数据来率定GR4J的参数，选取1985-1994年为验证期。4个参数的取值范围见表1[11]。

表1 GR4J参数边界Table 1 Ranges of parameters of GR4J

率定过程中，选取NS效率系数作为主要目标函数，采用自动率定。为了更好的评估模型对枯水的模拟，还计算了NS效率系数的对数形式[13]。采用相对误差RVE反映径流模拟值与实际值的关系,并计算了均方根值RMSE。

计算结果表明模型率定期和验证期的NS效率系数都高于0.8，径流对数形式下的NS效率系数也都达到了0.8，率定期和验证期RMSE分别为1.11和1.38，即该模型能有效的模拟径流，且在枯水模拟方面也有较好的效果。从RVE来看，GR4J模型对金华江流域的模拟值比实际值要偏小。为了更直观的了解径流模拟情况，选取比较有代表性的1983年比较流域径流的模拟值和实测值(图5)。

图5 1983年金华江流域径流GR4J模型实测值与模拟值比较Fig.5 Comparison of daily flow at Jinhua station in 1983

3.3 枯水指数分析

对枯水径流进行频率分析方法有很多种，枯水指数分析是其中应用最普遍的一种。常见的枯水指数，7Q2,7Q5，7Q10，7Q20等在工程应用和政策制定中发挥着重要的作用。指数中，7指7天连续径流，后面的数字则是特定的回归期。如7Q10是指10年一遇的7 d连续枯水径流的平均值。此外，还有一些根据不同连续天数制定的枯水指数,如30Q10，4Q3，90Q10等。本文选取了7Q10和30Q10作为标准分析未来的枯水指数。7Q10的应用较为广泛，如枯水设计参考，水质保护指标，污水处理参考依据，河滨生态保护参考指标以及水资源配置参考等。30Q10的用处与7Q10类似，但更侧重于水质[14]。使用Weibull分布分析基准期和预测期的径流[15]，得出的结果如表2和3所示。

表2 不同回归期连续7天最小平均流量
Table 2 Lowest average flows for a consecutive 7 day period of different return periods m3/s

项目回归期5a10a20a30a基准期5.793.862.622.09RCP2.612.7511.7210.8110.32RCP4.511.9310.619.488.89RCP6.012.0610.769.659.06RCP8.512.7011.4110.299.69

从表中可以发现，四个情景下的7Q10和30Q10都有增加，7Q10的变化更为剧烈。观察不同回归期下的数据发现，预测期的径流比基准期更为平稳。这也和预测径流时间序列情况相吻合。这意味着，在21世纪的最后30 a，金华江流域在枯水季节的水资源量可能增加。四个不同情景下，随着辐射强迫的增加，7Q10和30Q10都增加，但RCP2.6情景出现了异常，可能是由于辐射强迫较低，蒸发量较少导致。

表3 不同回归期连续30 d最小平均流量
Table 3 Lowest average flows for a consecutive 30 day period of different return periods m3/s

项目回归期5a10a20a30a基准期12.879.507.106.00RCP2.615.8114.5813.4812.89RCP4.514.6012.9511.5410.80RCP6.015.3613.8412.5311.83RCP8.515.8414.1612.7111.95

4 结 论

本文选取金华江流域为研究区域，使用GIST模型作为天气发生器，并用GR4J模型和CMIP5全球气候环流模式的未来数据预测了2071-2100年的径流，分析了枯水指数7Q10和30Q10的变化情况。计算结果表明，GIST能较好模拟流域的降雨和温度，并能保留其空间相关性。同时，GR4J在率定和验证时的目标函数都达到了0.85以上，因此可以认为在金华江流域使用该模型进行径流模拟是可行的。最后，本文对水文模型模拟的径流结果进行了频率分析，发现在21世纪末，各个回归期的枯水径流量增大。以7Q10而言，其在RCP2.6，RCP4.5，RCP6.0，RCP8.5四个情景下增加的幅度都超过了150%，最大变化幅度发生在情景RCP2.6，达到了203%。相对而言，30Q10的增幅较小，最大的变化同样出现在RCP2.6，达到了53%。这些结论可供政策制定者作出相关政策的参考。

[1] 杨涛, 陆桂华, 李会会, 等. 气候变化下水文极端事件变化预测研究进展 [J]. 水科学进展, 2011, 22(2): 279-286.

[2] 张建云, 王国庆, 杨扬, 等. 气候变化对中国水安全的影响研究[J]. 气候变化研究进展, 2008, 4(5).

[3] 王国庆, 张建云, 刘九夫, 等. 气候变化和人类活动对河川径流影响的定量分析[J]. 中国水利, 2008(2): 55-58.

[4] MOSS R H, EDMONDS J A, HIBBARD K A, et al. The next generation of scenarios for climate change research and assessment[J]. Nature, 2010, 463(7282): 747-756.

[5] SMAKHTIN V U. Low flow hydrology: a review[J]. Journal of hydrology, 2001, 240(3): 147-186.

[6] TIAN Y, XU Y P, ZHANG X J. Assessment of climate change impacts on river high flows through comparative use of GR4J, HBV and Xinanjiang Models[J]. Water Resources Management, 2013,27(8):1-18.

[7] Van VUUREN D P, EDMONDS J, KAINUMA M, et al. The representative concentration pathways: an overview[J]. Climatic Change, 2011, 109(1/2): 5-31.

[8] BAIGORRIA G A, JONES J W. GiST: A stochastic model for generating spatially and temporally correlated daily rainfall data[J]. Journal of Climate, 2010, 23(22): 5990-6008.

[9] ANANDHI A, FREI A, PIERSON D C, et al. Examination of change factor methodologies for climate change impact assessment[J]. Water Resources Research, 2011, 47(3):W03501.

[10] SIMONNEAUX V, HANICH L, BOULET G, et al. Modelling runoff in the Rheraya Catchment (High Atlas, Morocco) using the simple daily model GR4J. Trends over the last decades[C]//13th IWRA World Water Congress, Montpellier, France，2008.

[11] 田烨. 气候变化对极端径流影响评估中的不确定性研究[D].杭州： 浙江大学, 2013.

[12] 胡庆芳，杨大文，王银堂，杨汉波. Hargreaves 公式的全局校正及适用性评价[J].水科学进展.2011.22(2):160-167.

[13] KRAUSE P, BOYLE D P, BSE F. Comparison of different efficiency criteria for hydrological model assessment [J]. Advances in Geosciences, 2005, 5(5): 89-97.

[14] PYRCE R. Hydrological low flow indices and their uses[R]. Watershed Science Centre(WSC) Report, 2004.

[15] 周芬, 郭生练, 熊立华, 等. 枯水频率分析线型的比较研究[J]. 水文, 2006, 26(1): 28-33.