基于ANSYS和ISIGHT的EHA作动筒结构分析与优化

陈 辰，段富海

（大连理工大学机械工程学院，辽宁大连 116023）

0 引言

未来飞机向高速化、高压化、快速响应等方向发展，而随着飞机速度和其他性能的不断提高，飞机舵面承受的静动态载荷将会更大，偏转速率将会更快，这要求控制舵面精准偏转的作动器功率更大、结构强度更好。作动筒是作动器的关键部件，要承受主要静动态载荷，同时由于作动器在工作时要面临各种各样的工况，会通过振动、负载力、铰链力矩等形式在作动筒上产生交变动态载荷，都会对作动筒的静动态特性和稳健性产生较大的影响，从而影响作动器的使用性能。

在当前的功率电传机载作动系统中，电动静液作动器（Electro Hydrostatic Actuator，EHA）以其体积小、功率大、控制灵活等特点受到越来越大的关注，是当前先进飞机新作动系统研究的重点。

在EHA作动筒的受力状态分析、工况运行模拟方面，国内外研究报道不多。在设计高性能EHA产品时，有必要采用有效的有限元分析（Fi⁃nite Element Analysis，FEA）软件，对其结构进行分析，找出其可能存在的失效形式或设计缺陷，避免共振效应，并通过仿真优化等手段对作动筒进行结构优化，达到提高产品结构强度、可靠性和寿命，降低产品重量和成本的目的。

ANSYS是一种适合机械构件结构分析的大型通用FEA软件，能提供强大的实体建模及网格划分工具，能方便地构造有限元模型，能进行结构及优化分析，能将计算结果以彩色等值线图形方式显示。基于多学科设计优化(Multidisciplinary Design Optimization，MDO)框架的ISIGHT优化软件是过程集成、优化设计和稳健性设计的集成开放软件。使用ISIGHT的过程集成界面，可方便地将各种通用的CAD／CAE软件工具集成在一起，将各种优化方法有效地组织起来进行多学科优化设计[1]。

本文以电动静液作动器的作动筒为研究对象，使用ANSYS对其分别进行了载荷分析、模态分析和压杆稳定性分析。通过ISIGHT集成AN⁃SYS，以作动筒的质量最轻和变形最小为目标，同时满足静力约束和模态约束，建立了作动筒的优化模型，进行了优化设计，得出了优化结果。

1 EHA的工作原理和作动筒载荷要求

1.1 EHA的工作原理

EHA的工作原理如图1所示。

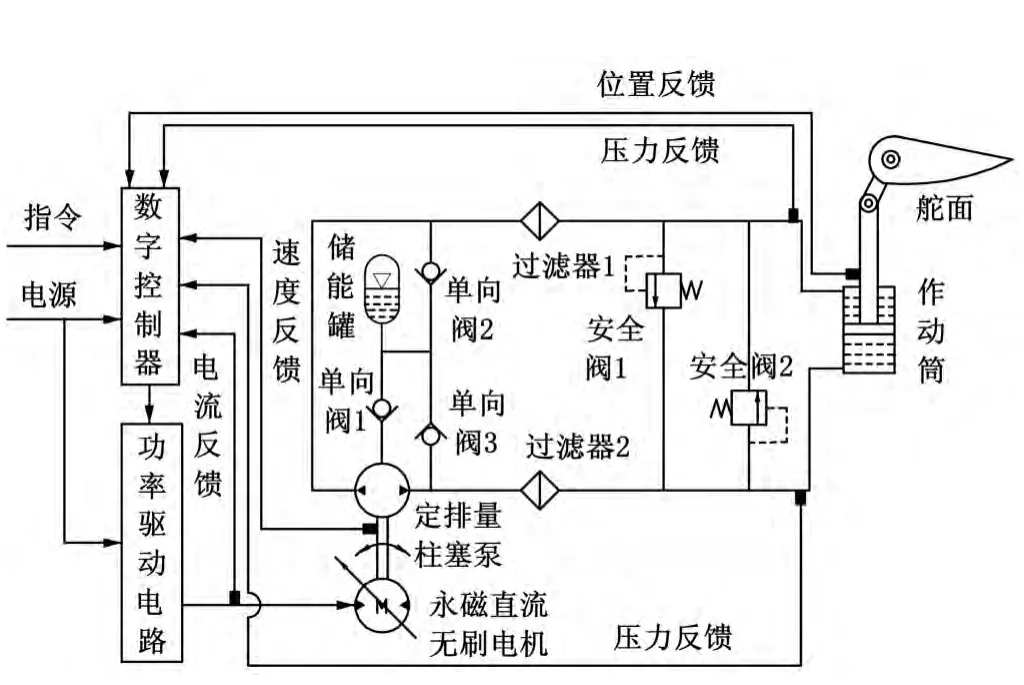
图1 EHA作动器原理框图

通过数字控制器和功率控制器组成的控制电路，控制永磁无刷直流电机的转速，通过电机带动高速双向定排量柱塞泵旋转运动，继而控制泵输出到作动筒的高压油的流量，以容积调速方式完成对作动筒的控制。电机的正反转控制作动筒的伸出和收缩运动，电机的转速控制作动筒的运动速度。

1.2 EHA的作动筒载荷要求

作动筒的静动态性能要求主要包括铰链力矩、限制/极限载荷、静态刚度、有载偏转速率、动态刚度特性和频率响应特性分析等[2]。

下面根据航空作动器规范，给出某型民用运输机方向舵EHA作动器作动筒的最大铰链力矩要求、限制载荷和极限载荷要求。

最大铰链力矩规定为舵面失速时可能承受的最大气动铰链力矩。某型民用运输机方向舵作动器最大铰链力矩出现在起飞滑跑阶段单发失效，舵面为+30°时。将该最大铰链力矩要求转化为作动器最大输出载荷为5×104N。

该型民用运输机方向舵作动器的限制载荷（Limit load）规定为作动器需经历限制载荷后无功能和性能降级，对应机械部件的计算要求为可允许弹性变形但不允许出现塑性变形和破裂。该型民用运输机方向舵作动器的极限载荷规定（Ulti⁃mate load）为作动器经历极限载荷后，不允许出现破裂，可接受出现一定的塑性变形。缸体中液压油取验证压力Pf=4 500 psig，用于校核限制载荷；取爆破压力Pb=7 500 psig，用于校核危险界面的极限载荷。将限制载荷和极限载荷换算为标准单位制分别为31.01 MPa和51.68 MPa。

2 基于ANSYS的作动筒有限元分析

2.1 作动筒的载荷分析

根据EHA作动器的最大输出载荷和液压油额定压力20.682 MPa（3 000 psig），可以设计出作动筒缸筒的内径为80 mm。根据经验公式，设计作动筒缸筒长度200 mm，缸筒厚度8 mm，活塞厚度56 mm，活塞杆直径60 mm，活塞杆长度400 mm。作用在活塞杆上的外力F＝5×104N，设置作动筒的材料密度、弹性模量、泊松比、许用抗拉强度分别为 ρ＝7.8×103kg/m3、 E ＝2×1011Pa、ν=0.3、 σb＝1 069 MPa。

用ANSYS建立作动筒有限元模型时，忽略了比较小的倒角和螺纹孔等，并对活塞杆两端的耳环、活塞和缸筒两端等关键部位的网格进行了细化处理。选用Solid95高阶三维实体单元作为计算单元，采用映射网格对模型进行划分，最后获得的有限元模型共有24 052个单元、14 247个节点。

Solid95高阶三维实体单元具有20个节点，每个节点有3个自由度，即转化为节点坐标系下的绕三个坐标轴方向的移动。Solid95单元可以在不损失精度的前提下很好地模拟不规则的几何形状，并且具有协调的位移函数，可以很好的模拟边界曲线。单元也可有任何的空间定位。通常情况下，Solid95高阶三维实体单元需要输入的材料参数有弹性模量、线膨胀系数、泊松比、密度、坐标系和阻尼。

约束是在耳环和缸底两处模拟实际的约束情况。活塞杆和耳环均为圆柱铰链，具有一个绕轴线转动的自由度。在有限元软件ANSYS中利用群组杆单元和位移约束来模拟[3]。

当在杆腔施加30.01 MPa的限制载荷时，结果如图2。作动筒的最大变形出现在活塞杆耳环处，其最大位移变形为0.098 mm＜0.1 mm（最大变形要求），满足要求。

图2 作动筒的位移变形图

当在杆腔施加51.68 MPa的极限载荷时，结果如图3。作动筒的最大应力出现在缸筒中部，最大应力为306 MPa＜1069 MPa，满足要求。

图3 作动筒的应力图

2.2 作动筒的模态分析

模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型，是设计承受动载荷的重要参数。通过模态分析结果图，可直观地表明机械产品的动态特性和薄弱环节，为产品的动力学优化设计提供直接的理论分析依据。

由于飞机在飞行过程中会产生颤振，为防止发生共振响应，导致疲劳裂纹，有必要对已经建立的作动筒有限元模型进行动模态特性分析，保证在优化过程中作动筒的频率稳定在一定范围内。

1阶模态是在外力的激励频率与物体固有频率相等的时候出现的，此时物体的振动形态叫做1阶振型或主振型；2阶模态是在外力的激励频率是物体固有频率的两倍时候出现，此时的振动外形叫做2阶振型，依次类推。工程实践证实，越是低阶的模态对系统的影响越大，许多机械结构在工作状态下，只有少数低阶模态起作用。

在模态分析过程中只在缸筒耳环处加固定约束，其他部位不施加约束，选用Block Lanczos模态提取方法[4-6]，提取作动筒的第1阶和第2阶模态如图4和图5，作动筒前6阶固有频率和最大变形量见表1。

图4 作动筒的第1阶模态

以上结果表明，作动筒振动主要表现形式为弯曲振动。当作动筒第1阶频率为138.52 Hz时，作动筒的最大变形量为523 mm，出现在活塞杆耳环部位，最大变形是由于活塞杆的变形所致，尤其是活塞杆和缸筒接触部位的变形比较明显。当作动筒第2阶频率为148.73 Hz时，作动筒的最大变形量为535 mm，也是出现在活塞杆耳环部位，变形原因跟第1阶时相似。

图5 作动筒的第2阶模态

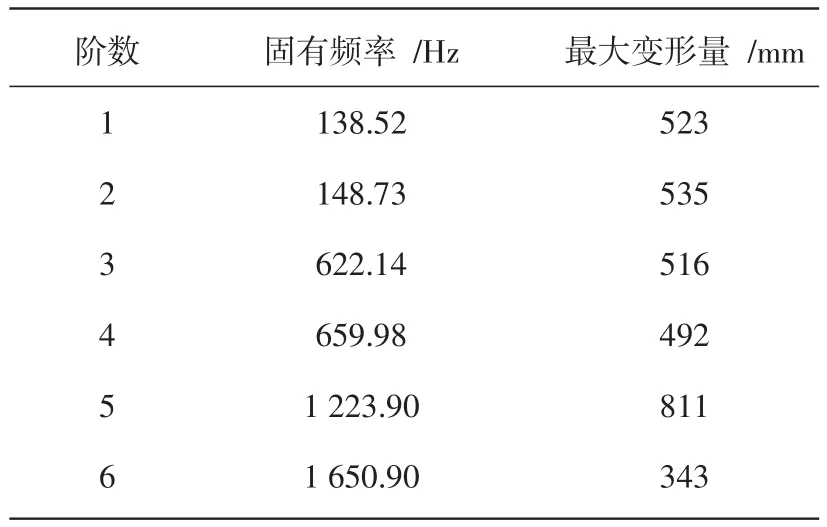
表1 作动筒前6阶固有频率和最大变形量

由于作动筒的部分模态比较密集，如1阶和2阶频率较低，作动筒在低频内的激励也比较大，很容易发生共振响应，导致疲劳裂纹。同时，1阶和2阶、3阶和4阶固有频率差较小，容易引起相邻模态的耦合振动。

分析可知，活塞杆在低阶振动时沿径向的变形比较大，可通过加大直径尺寸或变更材料等措施加以改进。

2.3 作动筒的压杆稳定性模拟分析

当细长杆受压时，轴线不能维持原有直线形式的平衡状态而突然变弯的现象，称为失稳。这种破坏是突发性的，往往会给工程结构或机械带来极大地损坏。作动筒活塞杆是细长杆结构，在工作过程中承受较大的压力，需要综合作动筒实际工作状况，对其压杆稳定性的进行校核与分析。

在ANSYS环境下，压杆稳定性主要通过屈曲分析完成。屈曲分析用于确定结构开始变得不稳定时的临界载荷和屈曲结构发生屈曲响应时的模态形状。作动筒活塞杆通常在结构强度还远没达到极限时就发生了屈曲。

屈曲分析只针对需要进行稳定性分析的活塞杆，材料属性跟载荷分析时一致。首先在活塞杆底部加全固定约束，在耳环圆孔下边施加1Pa的载荷，进行单位压力下模型的静态预应力的计算。然后选用子空间迭代法（Subspace）进行特征值屈曲分析的求解，Subspace法虽然速度相对较慢，但精度较高。一阶屈曲形态变形图见图6。

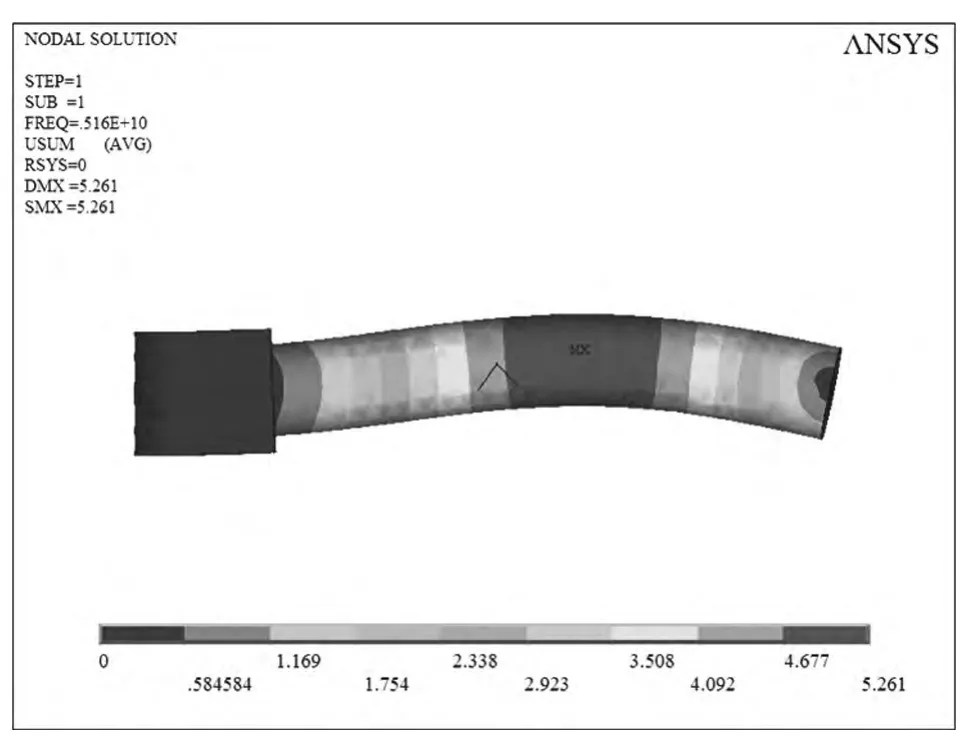
图6 一阶屈曲形态变形图

图6 中，屈曲载荷系数FREQ=0.516×1010，而实际加载值为1 Pa，屈曲分析所得的临界值等于屈曲系数乘以实际加载值，故临界载荷为5 160 MPa，此载荷远远大于材料的许用抗拉强度σb＝1 069 MPa，故此活塞杆结构稳定，不易发生屈曲变形。

3 基于ISIGHT的EHA作动筒优化

3.1 作动筒的结构优化模型

选择作动筒缸筒壁厚T1、缸筒长度L1及活塞杆直径D2、活塞杆长度L2和活塞厚度T2作为设计变量。设计变量需要满足以下设计条件和约束要求[7]：

缸筒壁厚需要满足校核条件

其中：D1为缸筒内径；Pt为缸筒实验压力，当缸筒额定压力Pn≥16 MPa时，取Pt=1.25Pn；[σ] 为缸筒材料的许用应力，[σ]=σb/n， σb为材料的抗拉强度，σb＝1 069 MPa，n为安全系数，一般取n=5。将各数值带入式中，得T1≥4.83 mm。

根据最大工作行程，要求缸筒长度范围为150 mm≤L1≤400 mm。

根据作动器行程，要求活塞杆长度范围为300 mm≤L2≤600 mm。

活塞杆直径需要满足的校核条件：

其中：F为输出载荷；[σ1]为活塞杆材料的许用应力，[σ1]=σb1/1.4。同时根据设计要求0.5D1≤D2≤D1，综上40 mm≤D2≤80 mm 。

活塞的厚度T2作为设计变量一般为（0.6～1） D1，故48 mm≤T2≤80 mm。

根据设计要求，作动筒在满足最大压缩工况下的最大应变小于0.1 mm，在极限载荷作用下应力不超过强度极限。为使结构的刚柔度保持在合理范围内，保证优化后作动筒的模态频率处在一个稳定的区间内，设定优化前的第1阶模态频率值减小30 Hz，约为110 Hz，作为下限，第2阶模态频率值增加30 Hz，约为180 Hz，作为上限。优化目标为作动筒的质量最轻，变形最小。

作动筒的结构多学科设计优化问题描述如下：

优化目标：

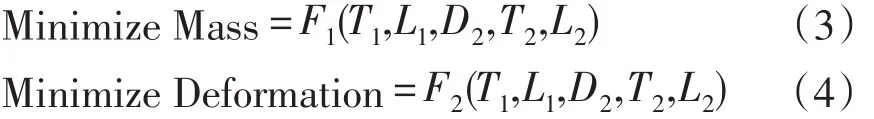
约束条件：

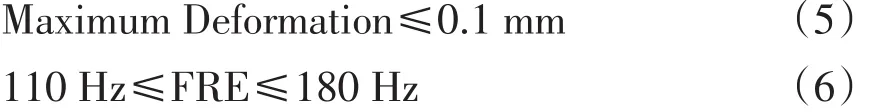
作动筒的设计变量见表2。

表2 作动筒的设计变量

3.2 基于ISIGHT的作动筒优化

应用基于MDO框架的ISIGHT软件对作动筒进行结构优化时，首先要将ANSYS集成于ISIGHT平台。然后根据数学模型进行参数的设置：包括变量、目标函数、约束函数及优化方法选择。优化时选用ISIGHT内嵌的NLPQL序列二次规划算法[8]。

优化运行结果如图7和图8所示。

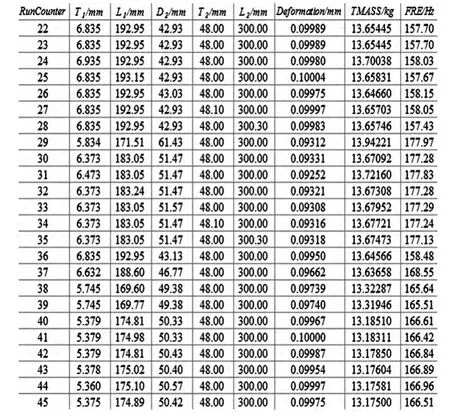
图7 作动筒优化过程部分变量数据截图

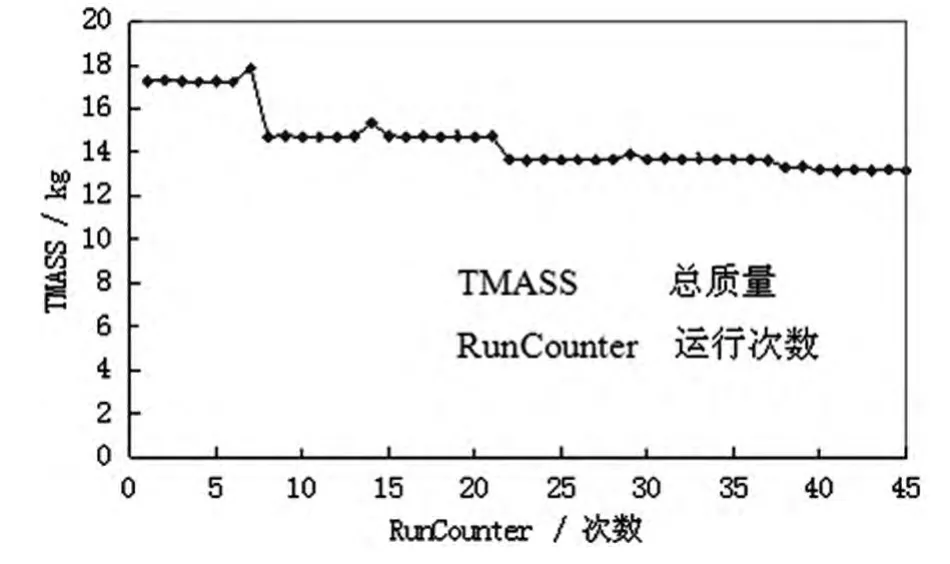
图8 作动筒质量优化过程图

优化结果：作动筒缸筒长度174.89 mm，作动筒缸筒厚度5.38 mm，活塞厚度48 mm，活塞杆直径50.42 mm，活塞杆长度300 mm，变形量0.099 75 mm，质量mass＝13.18 kg。质量比于优化前的质量17.25 kg，减少了23.5%。

4 结论

以飞机电动静液作动器作动筒为研究对象，采用ANSYS软件对EHA的作动筒进行了载荷、模态和压杆稳定性等有限元分析。通过ISIGHT集成ANSYS，对作动筒进行了结构优化设计，取得了较好的优化效果。结果表明，用ISIGHT进行作动筒优化设计，工作量小、求解简单方便，得到的作动筒设计参数更为科学合理。

本文的分析和优化方法，可为大型机器人手臂的作动器和工程机械的液压缸设计提供借鉴。

［1］ Fengtao Wei，Li Song，Yan Li，Peng Liu.Application of ISIGHT in solving multi-objective optimal design prob⁃lems［C］.Consumer Electronics，Communications and Networks（CECNet），XianNing，2011：110-113.

［2］沈磊.民用飞机电传飞控作动系统设计与工程运用［D］.上海：上海交通大学，2012.

［3］李晓东.工程机械液压缸有限元分析研究［D］.长春：吉利大学，2012.

［4］ Shouguang Yao，Shengchen Zhao，Fei Liu.Finite ele⁃ment analysis and multidisciplinary design optimization of diesel engine connecting rod based on ISIGHT ［J］.Ad⁃vanced Materials Research， 2012， 479 （481）：1863-1867.

［5］杨为，邱清盈，胡建军.机械结构的理论模态分析方法［J］.重庆大学学报，2004，27（6）：1-4.

［6］王宇，刘凯，林永龙.ANSYS软件在结构模态分析中的应用［J］.机电工程技术，2013（9）：38-40.

［7］王积伟.液压传动［M］.北京：机械工业出版社，2006.

［8］胡文婕，陈亮.基于ISIGHT的汽车盘式制动器多学科设计优化［J］.农业机械学报，2010，41（5）：17-20.