具有第三大边平均Wiener指标的单圈图

苏晓海， 杨立夫

(陕西理工学院 数学与计算机科学学院， 陕西 汉中 723000)

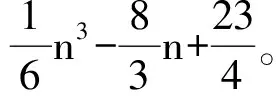
本文所涉及的图都是简单的无向连通图。设图G的顶点集和边集分别记为V(G)和E(G)，|V(G)|和|E(G)|分别表示图G的顶点数(阶数)和边数。一个图G的圈数λ定义为λ=|E(G)|-|V(G)|+1，λ=1的图称为单圈图。如果u和v是图G的两个顶点，则连接它们的最短路的边数称为这两点之间的距离，记为d(u，v)。设f=uv，g=xy是图G的两条边，则f和g的平均距离记作D′(f，g)，定义为

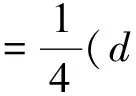
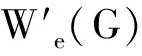
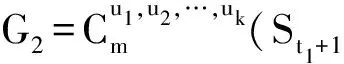
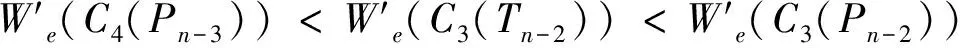
等号成立当且仅当G≅C4(Pn-3)，所以当n>10时具有第三大边平均Wiener指标的n阶单圈图是C4(Pn-3)(见图1)。

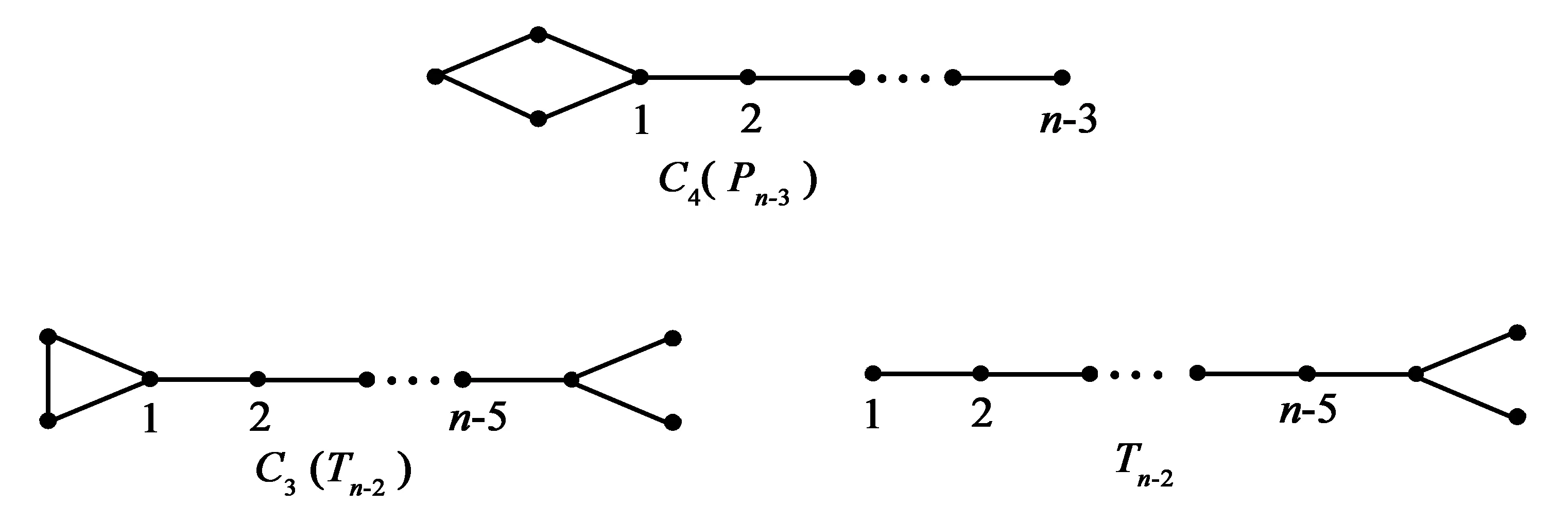
图1 单圈图C4(Pn-3)、C3(Tn-2) 及其子图Tn-2

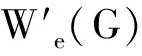
从而

,(n>10),

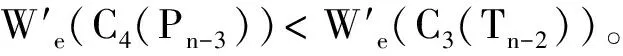
分两种情况证明：

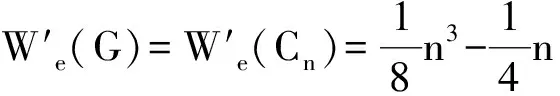
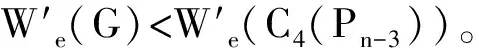
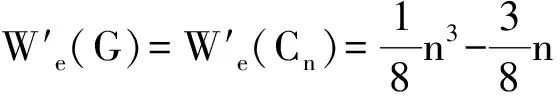
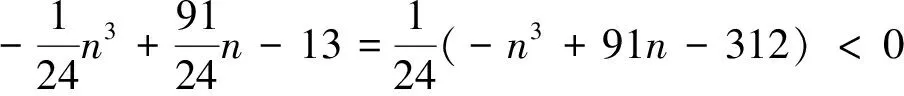
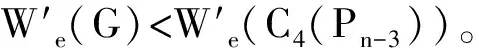
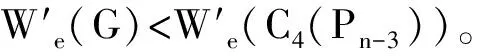
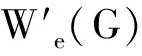
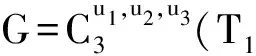
由于n>10，m=3，故k取值只可能是1，2或3。

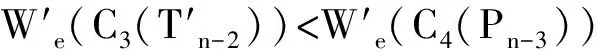
图2 单圈图 及其子图

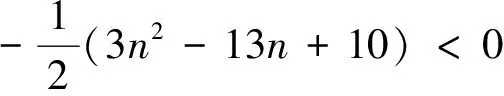
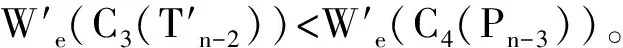
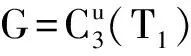
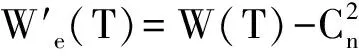
又因为

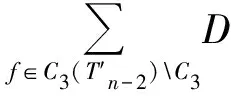
所以

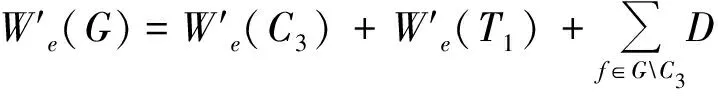
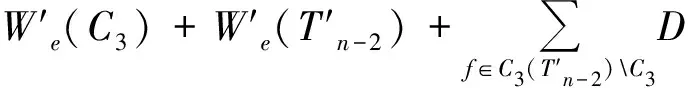
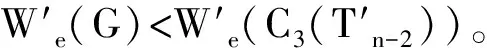
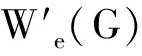
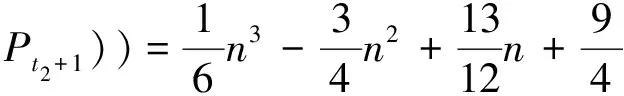
由于

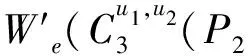
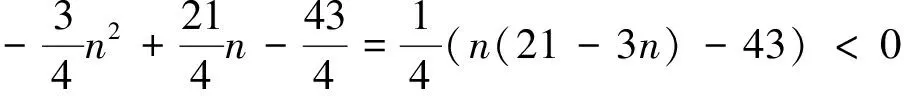
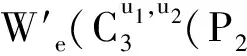
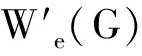
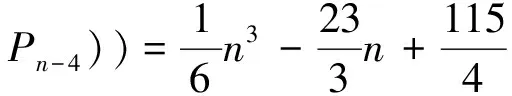
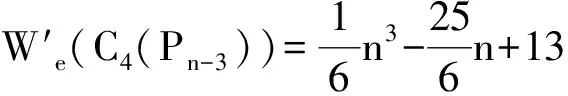
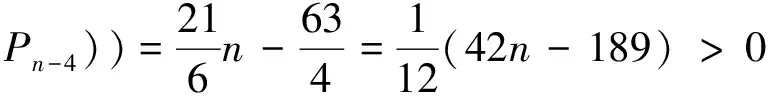
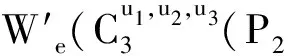
综上所讨论可知，当n>10时，

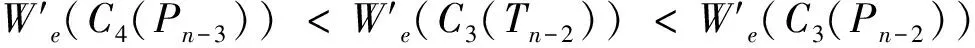
且等号成立当且仅当G≅C4(Pn-3)。所以，当n>10时具有第三大边平均Wiener指标的n阶单圈图是C4(Pn-3)。定理得证。

[参考文献]

[1] 蔡华.图的边平均Wiener指标[D].乌鲁木齐：新疆大学，2009.

[2] 苏晓海.具有次大边平均Wiener指标的单圈图[J].陕西理工学院学报：自然科学版，2013，29(5)：75-78.

[3] BERTZ S H，WRIGHT W F.The graph theory approach to synthetic analysis：definition and application of molecular complexity and synthetic complexity[J].Graph Theory Notes，1998(35)：32-48.

[4] ESTRADA E，GUEVARA N，GUTMAN I.Extension of edge connectivity index Relationships to line graph indices and QSPR applications[J]. J. Chem. Inf. Comput. Sci.，1998(38)：428-431.

[5] GUTMAN I. Distance of line graphs[J].Graph Theory Notes，1996(31)：49-52.

[6] 苏晓海，王力工.两类图及其线图的Wiener指标[J].山西大学学报：自然科学版，2011，34(3)：397-401.

[7] 于玲，叶永升.路和圈的联的Wiener指数[J].淮北师范大学学报：自然科学版，2011，32(1)：1-3.

[8] 陈娅红.关于单圈图的Wiener指数[J].丽水学院学报，2010，32(5)：14-16.

[9] 邢抱花.单圈图的Wiener指数的若干性质[J].合肥学院学报：自然科学版，2008，18(2)：14-17.

[10] 汤自凯.具有次大Wiener指数的单圈图[J].湖南文理学院学报：自然科学版，2006，18(4)：2-5.