一类半线性椭圆问题非平凡解的存在性
2014-03-26高婷梅
高婷梅
(陕西理工学院 数学与计算机科学学院, 陕西 汉中 723000)
1 主要结果
考虑下面的Dirichlet边界值问题
-△u+b(x)u=f(x,u),x∈Ω,u=0,x∈∂Ω,
(1)
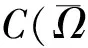
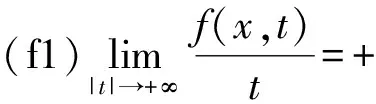
在文献[1]中,作者在(AR)条件成立的前提下研究了方程(1):

此(AR)条件对于证明相应的泛函具有山路几何结构和相应的(PS)c序列有界时起着至关重要的作用, 但它却不包含一些超二次非线性项, 例如
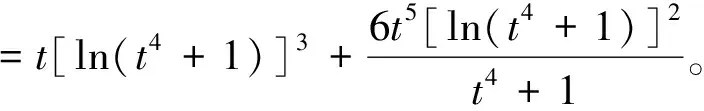
为了克服缺失(AR)条件带来的困难,很多数学家作出了努力,可见文献[2-8]。本文中, 假设条件(f1)成立,在缺乏(AR) 条件的情况下证明方程(1)存在非平凡解。下面给出本文的主要结果。
定理假设f(x,t)满足(f1)和以下条件:
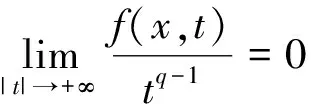
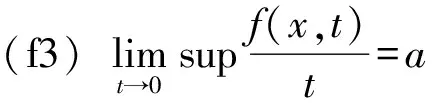
(f4) 存在常数θ≥1,θ0>0使得θG(x,s)≥G(x,t)-θ0对所有的x∈Ω,0≤t≤s都成立, 其中G(x,t)=f(x,t)t-2F(x,t)。
则方程(1)至少存在一个非平凡解。
注:文献[9-10]中,在缺乏(AR)条件的情况下,利用局部环绕定理(见文献[1])证明了方程(1)至少存在一个非平凡解,但是却假设以下条件成立:
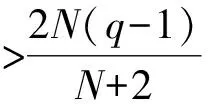
显然, 条件(f4)不同于条件(f0);其次,本文利用了条件(f3),由于0≤a<+∞, 这包含了文献[9-10]中的情形。
2 定理的证明
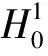
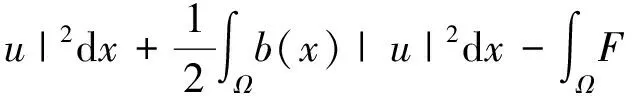
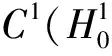
由条件(f3),常数a<+∞,可以分成两种情况:
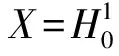
,e2,…,en},n∈N,
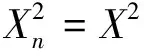
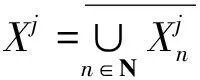
(a) 证明I在0处关于(X1,X2)局部环绕,即存在δ0>0,使得
I(u)≤0,∀u∈X2且‖u‖≤δ0,
I(u)≥0,∀u∈X1且‖u‖≤δ0。
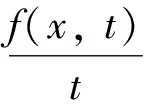
λk-1st2≤tf(x,st)≤λkst2。
(2)
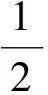
因为dimX2<+∞,则存在C1>0,使得
‖u‖∞≤C1‖u‖, ∀u∈X2,
所以由式(2)可知
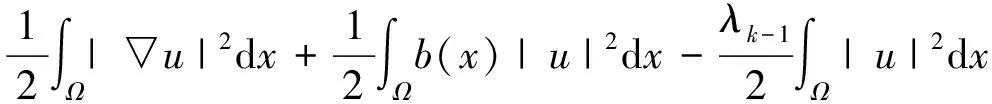
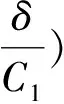
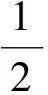
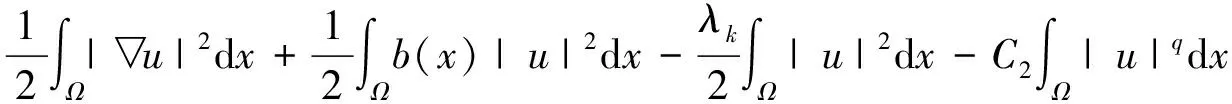
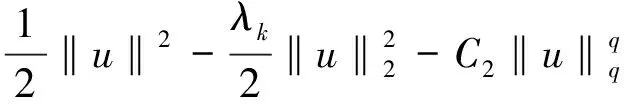
其中C3>0是一个常数。因为q>2,则对所有的u∈X1,当‖u‖足够小时,有I(u)≥0。
(b) 证明I满足(PS)*条件。
假设{uαn}是一个使得αn可容许的序列,并且满足
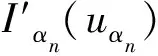
(3)
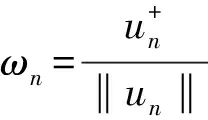
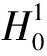
ωn→ω在L2(Ω)中,
ωn(x)→ω(x), a.e.x∈(Ω)。
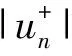
∞, a.e.x∈Ω+,
上式可以推出
→+∞,n→+∞, a.e.x∈Ω+,
(4)
由条件(3),有
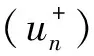
所以
≤1+C4‖b‖∞≤C0,
其中C4,C0>0是常数。这和(4)式矛盾。
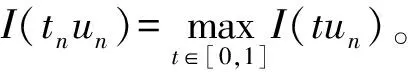
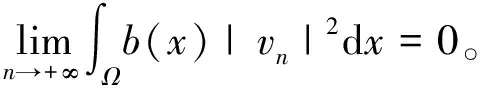
(5)

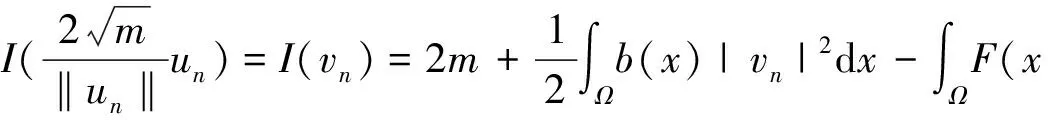
由上式可得
I(tnun)→+∞,n→+∞。
(6)
注意到I(0)=0且I(un)≤c,因此当n充分大时tn∈(0,1)。所以
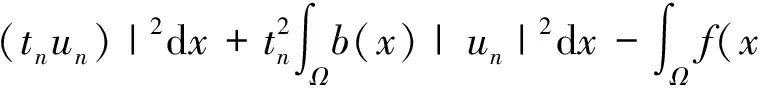
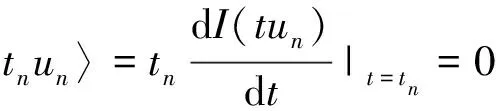
从而
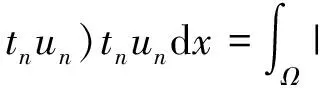
(7)
因为0≤tn≤1,所以|tnun|≤|un|,连同 (f4),(6)以及(7)式可以得到,当n→+∞时,
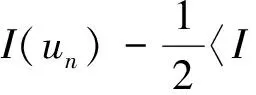
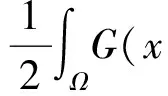
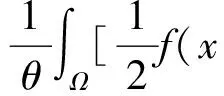
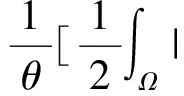
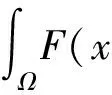
(8)
然而由(3)可知
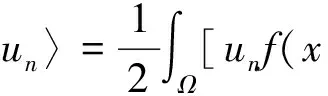
这和(8)式矛盾。所以{un}有界。
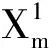
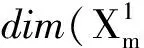
F(x,t)≥M1t2-M2, ∀(x,t)∈Ω×R,
所以
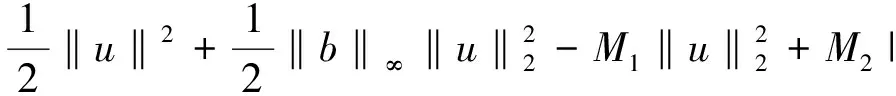
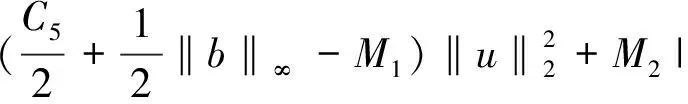
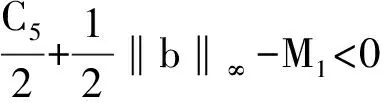
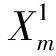
利用局部环绕定理,方程(1)存在一个非平凡解。
Ⅱ 假设0≤a<λ1,利用一个变化的山路引理(见文献[11])证明定理。
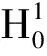
由条件(f2)和(f3),对任何ε>0,存在A>0使得

上式结合Poincare不等式和Sobolev不等式可得
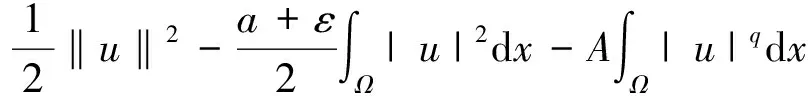
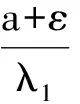
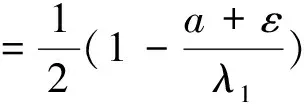
则有
I|∂Bρ≥β>0。
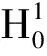
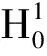
(c′)证明泛函I满足(C)条件。
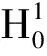
I(un)→c, (1+‖un‖)‖I′(un)‖→0,n→+∞,
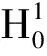
利用变化的山路引理, 可以得到方程(1)的一个非平凡解。
定理得证。
[参考文献]
[1] LI Shu-jie,WILLEM M.Application of local linking to critical point theory [J].J Math Anal.Appl.,1995,189:6-32.
[2] DEGIOVANNI M,Lancelotti S.Linking over cones and nontrivial solutions forp-Laplacian equations withp-superlinear nonlinear [J].Ann. Inst. H.Poincare Anal. Non Lineaire,2007,24:907-919.
[3] DINCA G,JEBELEAN,MAWHIN J.Variational and topological methods for Dirichiet problems withp-Laplacian [J].Port.Math.,2001,58:339-378.
[4] FAN X L,LI Z C.Linking and existence results for perturbations of thep-Laplacian[J].Nonlinear Anal.,2000,42(8):1413-1420.
[5] PERERA K.Nontrivial critical groups inp-Laplacian problem via the Yang index Topol [J].Methods Nonlinear Anal.,2003,21:301-309.
[6] WANG Z Q.On a superlinear elliptic equation [J].Ann.Inst.H.Poincare Anal.Non Lineaire,1991,8:43-57.
[7] BARTOLO P,BENCI V,FORTUNATO D.Abstract critical point theorems and applications to some nonlinear problems with“strong”resonance at infinty[J].Nonlinear Anal,1983,7:981-1012.
[8] COSTA D G,MAGALHAE C A.Variational elliptic problems which are nonquadratic at infinity[J].Nonlinear Anal,1994,23:1401-1412.
[9] OU Zeng-qi,TANG Chun-lei.Existence of solutions for a class of semilinear elliptic equations [J].Journal of Southwest China Normal University :Natural Science,2007,32(1):1-5.
[10] JIANG Qin,TANG Chun-lei.Existence of a nontrivial solution for a class of superquadratic elliptic problems [J].Nonlinear Analysis,2008,69:523-529.
[11] SCHECHTER M.A variation of the mountain pass lemma and applications [J].Journal of the London Mathematical Society,1991,44(3):491-502.
