一类含参数相似广义互联系统的鲁棒控制

孙延修

(沈阳工学院 基础课部， 辽宁 抚顺 113122)

相似广义互联系统是一种特殊的大系统，在航天、管理等领域广泛存在，而系统的稳定性是系统能够正常工作的前提。本文以广义系统[1]和相似性的研究为基础，研究了一类含参数相似广义互联系统的稳定性。研究的系统互联项是非线性的且含有不确定参数，由于系统本身具有相似结构这一特性从而在很大程度上简化了对其控制器的设计。本文参考了文献[2-3]中对不确定相似系统状态反馈控制器的设计与文献[4-5]中对不同类型控制器的构造，根据含参数广义互联大系统本身的特殊结构，以定理的形式给出了设计状态反馈控制器的条件。最后，在定理的证明中构造出了一种能够使系统渐近稳定的状态反馈控制器，使定理得以证明。

1 含参数相似广义互联系统的描述

考虑如下一类含参数相似广义互联系统：

(1)

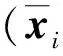
定义2[4]如果存在矩阵E,A,B,Ki和n阶非奇异矩阵Ti,Si，使得TiEiSi=E,TiBi=B,Ti(Ai+BiKi)Si=A，则称系统(1)具有相似结构，其中(Ti,Si,Ki)称为第i个子系统的相似参量。

假设1 对于任意的初始状态和控制输入系统(1)是正则的，且存在容许控制。

引理1[2]若任一标称子系统(Ei,Ai,Bi)能控，则系统(1)具有相似结构。

引理2[4]若系统(1)具有相似结构，标称子系统(Ei,Ai,Bi)稳定且脉冲可控，则系统(E,A,B)稳定且脉冲可控。

考虑系统(1)，假设存在相似参量(Ti,Si,Ki)使得TiEiSi=E，Ti(Ai+BiKi)Si=A，TiBi=B，i=1,2,…,N，即系统(1)具有相似结构，则可对系统做如下变换：

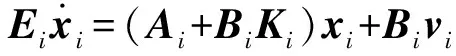
假设系统(E,A,B)稳定且脉冲可控，则存在矩阵K及非奇异矩阵T和S，使得下式成立：

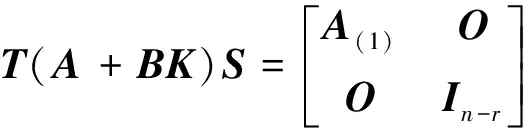
2 主要结果

定理1 如果系统(1)满足如下条件：

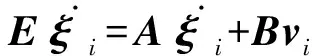
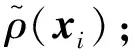
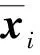
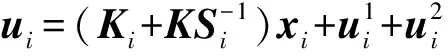
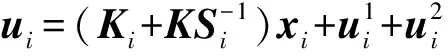
设ξi=Sηi，将其代入上式，然后由引理2存在非奇异矩阵T∈Rn×n，等号两边左乘T得：

慢子系统部分可写成：

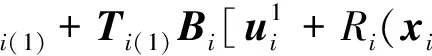
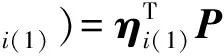
生活化的小学品德与社会课堂教学的实现不仅仅是在教学形式上的创新，而是一个涉及教学方法、教学理念、教材内容、教学目标以及教学计划等方面的体系化的工程。现阶段，很多教师的生活化教学仍然处于简单地照搬教学形式的层面，小学品德与社会课堂教学生活化浮于表面，形式主义严重是一个亟待解决的问题。小品表演、模拟采访等是生活化教学的方式之一，但是在教学活动开展的过程中，这些形式往往会成为一层外衣，其下包裹着的却是传统的教学理念和内容，实际上是换汤不换药，形式与内容严重脱节。形式主义的倾向严重影响到了生活化的课堂教学的效果，课堂教学的有效性不升反降。

所以可得如下不等式：

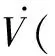
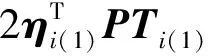
其中：

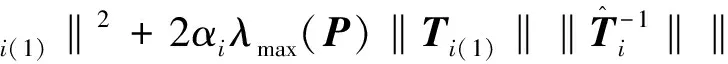
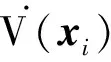
通过上述李亚普诺夫函数的性质及系统的相似性，可得系统(1)的李亚普诺夫函数为：

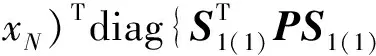
使得系统(1)在Ω的邻域内渐近稳定。

3 结束语

本文研究了一类含参数相似广义互联系统，并针对所研究的系统设计出了具有相似结构的鲁棒控制器。研究表明，含参数的相似广义互联系统的相似结构使其控制器具有相似结构，可以大大简化对控制器的设计。

[参考文献]

[1] 杨冬梅,张庆灵,姚波,等.广义系统[M].北京:科学出版社,2004.

[2] 严刚星.复杂相似组合系统的鲁棒全息控制理论与设计[M].西安:西北工业大学出版社,2000.

[3] 石海彬,张严心,刘晓平,等.一类具有相似结构的不确定非线性广义互联系统的鲁棒控制[J].控制与决策,2001,16(6):859-863.

[4] 石海彬,张嗣瀛.具有相似结构的广义互联系统的鲁棒控制[J].控制理论与应用,2003,20(2):265-268.

[5] 孙延修,任其昇.一类含参数的相似广义互联系统控制器的设计[J].沈阳大学学报:自然科学版,2012,24(1):28-29.