生物组织折射率分布的P偏光测量研究

娄本浊， 孙彦清， 黄朝军， 龙姝明， 赵升频

(陕西理工学院 物理与电信工程学院， 陕西 汉中 723000)

0 引 言

近年来随着生物产业的迅速发展，正确快速地分辨不同种类的透明生物组织及其形状与构造，对于研究溶液中不同透明生物组织的性质是非常重要的[1-2]。传统的检验技术[3-4]常常需要通过染色、扫描等方式来完成，不仅耗时，最主要的是会破坏组织本身的结构，因此，寻找一种简单、快速且不具破坏性的方法十分迫切。光学检测技术因其非侵入性、非接触性、快速方便等优点被广泛应用于生物学、生理学及医学等领域[5]。P偏光以布鲁斯特角入射有个非常重要的特性，即反射光强度趋近于零，利用此特性可以测量待测物体的折射率[6]。若将未知折射率的待测物放置于水中，可先算出空气与水界面的布鲁斯特角，这样在水与空气的界面上便没有反射光的产生，反射光只来自待测物体，再利用菲涅尔公式即可求取反射光强与折射率的关系，进而求出待测物体的折射率。故此，本文提出一种利用P偏光以布鲁斯特角入射来消除界面的反射光，并且利用反射光强的不同来获取透明物质折射率分布的方法，给出强度测量的原理与实验系统，详细讨论实验结果及误差来源。

1 测量原理

为探讨P偏光以布鲁斯特角入射时反射光强与折射率之间的关系，将待测透明物质放在水面上以满足实际检测需求，如图1所示。

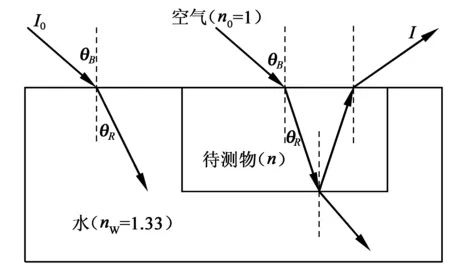
图1 P偏光在分界面的反射与折射

若P偏光以空气-待测物的布鲁斯特角入射，则待测物第一层的反射光强为零，只剩下透明物体的第二层与水面的反射光；而水与空气界面上的反射忽略不计，因为只要水的厚度增加，此处反射光强趋近于零，则菲涅尔公式[7]可表示为：

(1)

因此，待测物的反射率可表示为：

(2)

其中R为空气与待测物界面的反射率，r为振幅反射系数，n和n0分别为待测物和空气的折射率，θB为空气-待测物的布鲁斯特角，θR为折射角。利用折射定律[8]可将cosθR表示为：

(3)

结合式(2)与式(3)，可得反射光强与待测物折射率之间的关系为：

(4)

式(4)两边平方化简，即可由反射光强反演出待测物的折射率：

(5)

设入射光强度I0=1，并将空气折射率n0=1代入式(5)，式(5)可简化为：

(6)

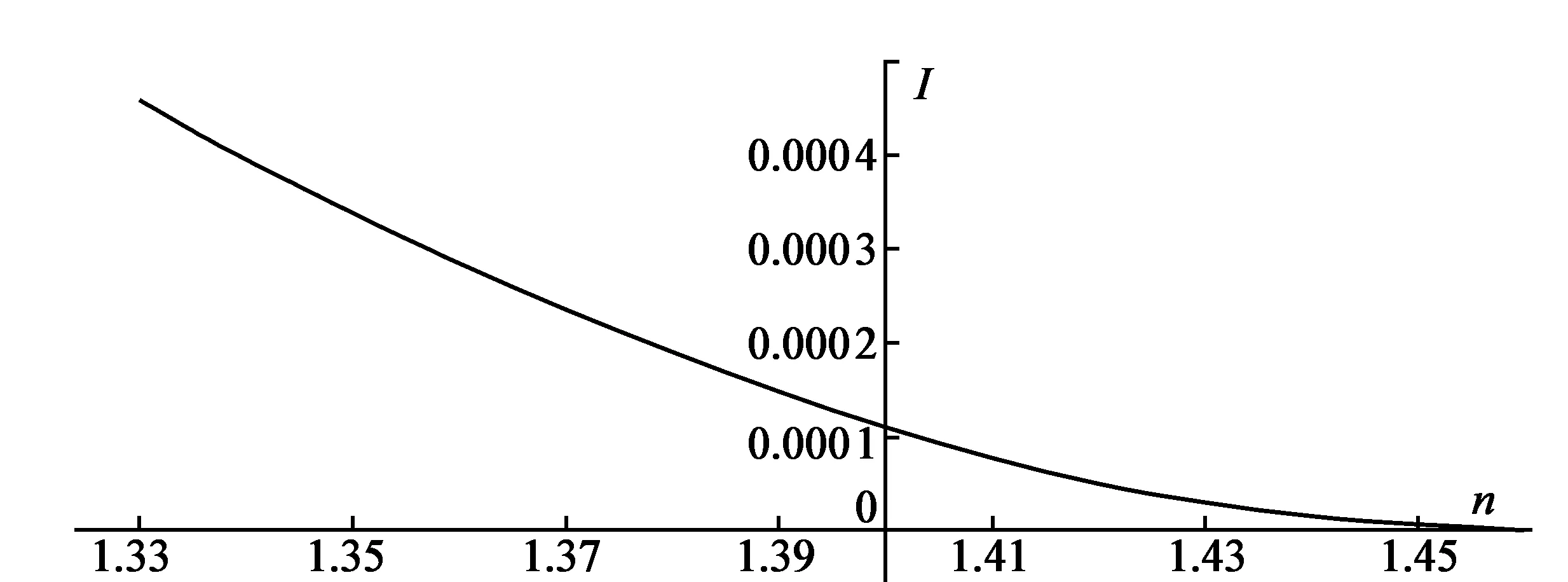
图2 待测物折射率与其反射光强之间关系的模拟结果

将空气-婴儿油的布鲁斯特角θB=55.59°及透明物体的折射率n的范围1.33～1.46代入式(6)，可模拟出反射光强I与透明生物组织折射率n的关系，如图2所示。

从图2可看出：待测物的折射率越大，反射光强就越小；当透明物体的折射率为1.46时，透明待测物即为婴儿油，其反射光强为零，光全部透射至水下。

2 实验系统设计

如图3所示，从功率为30 mW的LCM-LL-250型固态激光器发出的波长为532 nm的光经扩束器后成为平行扩束光，扩束光被平面镜反射后再经过起偏器变为P偏光；P偏光以空气-待测物界面的布鲁斯特角入射至待测物上被再次反射，因此处产生的反射光强较弱，故用PMTH-S1-1P28型光电倍增管(PMT)来接收，最后直接在与PMT相连的计算机中利用事先编写的程序反演出待测物的折射率分布。为了更接近实际检测时避免对待测物本身的损伤，在实验中选取功率较小的激光器作为光源。另外，待测物的反射光强对布鲁斯特角的选定非常敏感，当角度恰好为布鲁斯特角时，界面的反射光强度为零；而当角度稍微偏离布鲁斯特角时，界面反射光则会明显提高。所以在搭建实验系统时需注意以下几方面：首先，入射光必须为P偏光；其次，入射光在实验过程中必须平行；最后，入射光入射到待测物上的角度必须为实验所选定的布鲁斯特角。满足以上三点可大幅度提高实验精度。

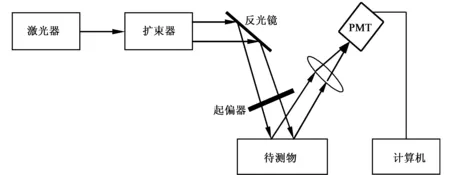
图3 实验系统结构简图

3 结果与分析

由于油水混合溶液一般是透明的且难以用肉眼观察其分布，类似于生物组织，故能取代透明生物体应用于验证本文所提技术可行性与系统可靠性的实验中。在此将折射率为1.46的婴儿油置于水面上作为待测物，利用第二部分所描述的实验系统进行测量；将测得的反射光强分布结果代入式(6)中，直接在计算机中用事先编写的程序进行反演，即可得到待测物的折射率分布图，如图4所示。

从图4可明显分辨出婴儿油与水的差别，图中颜色较浅(即反射光强较小)的部分为折射率较大的物相，而颜色较深(即反射光强较大)的部分为折射率较小的物相。这一实验结果与第二部分理论模拟结果相一致，但婴儿油在水界面处并不是规则的平面，会有一定的散射光产生。

首先，待测物折射率的改变会带来实验误差。将式(3)对待测物的折射率n微分，可得：

(7)

将n=1.33、n0=1及θB=55.59°等实验条件代入式(7)，可得反射光强变化△I与待测物的折射率变化△n之间的关系，如图5所示。由图5可知反射光强变化△I为0.001且n为1.33时，对应的折射率变化△n为0.044。

其次，入射角变化也会造成实验误差。将式(3)对θB微分，可得反射光强与入射角变化之间的关系：

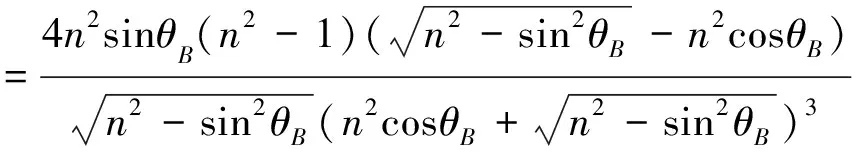
(8)

将上述实验条件等代入式(8)，所得结果如图5所示。由图5可知，当反射光强变化△I为0.001且n=1.33时，对应的入射角变化△θ为0.011°。将此结果与反射光强变化对折射率变化作比较，可知，当角度变化△θ=0.011°时，相当于折射率变化△n=0.044。可见在此样品的实验解析度中入射角变化△θ非常小，故可不考虑△θ的影响，因此当待测物的折射率n=1.513时，该技术实验解析度可达0.044。

4 结 论

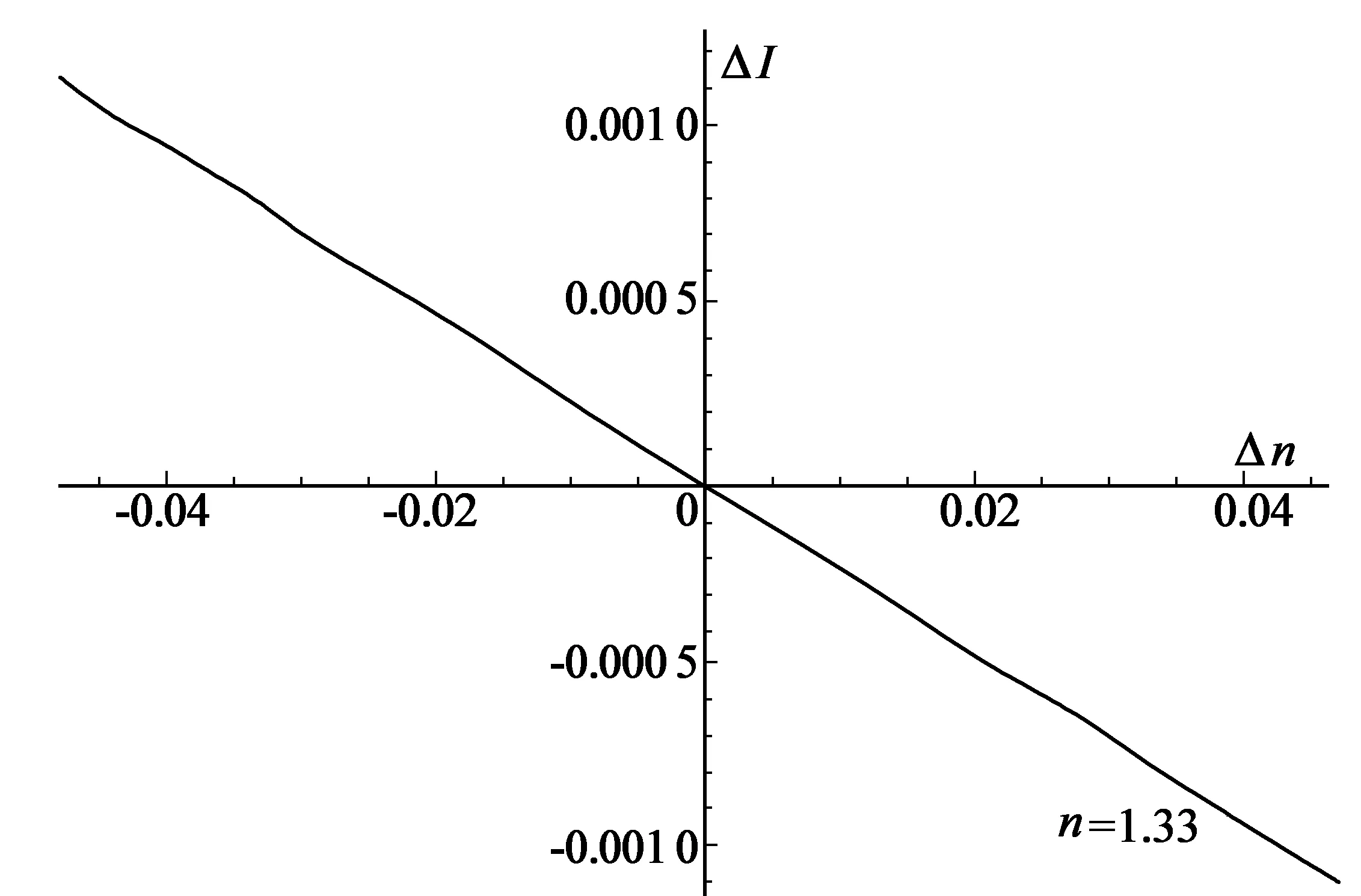
图5 待测物折射率变化与其反射光强变化的关系

本文详细推导了P偏光以布鲁斯特角入射时，透明生物组织的反射光强与其折射率之间的关系；基于理论推导设计搭建了一套实验系统，并用其测量了透明物质的折射率分布，所得结果与理论模拟结果相吻合。这表明利用本文所提技术与实验系统测量透明生物组织的折射率分布是可行的，它不仅能分辨平面上具有不同折射率的物相及其分布，而且利用布鲁斯特角的特性还可消除空气与待测物界面上的反射光，直接测量待测物的反射光强而获取其折射率分布。该方法具有简单快速、非破坏性和非侵入性等优点，可避免不必要的表面反射光，适用于长时间监测透明生物组织的折射率变化以及环境改变对生物组织的影响。

[参考文献]

[1] 冯盛,刘松,张学龙.生物组织对X射线的折射率因子[J].中国医学物理学杂志,2008,25(3):660-663.

[2] XU M,ALFANO R R.Fractal mechanisms of light scattering in biological tissue and cells[J].Optics letters,2005,30(22):3051-3053.

[3] ALEXA L M,SANFORD M S,JOSHUA Z R.Imaging with total reflection fluorescence microscopy for the cell biologist[J].Journal of cell science,2010(21):3621-3628.

[4] MOH K J,YUAN X C,BU J,et al.Surface plasmon resonance imaging of cell-substrate contacts with radially polarized beams[J].Optics express,2008,16(25):20734-20741.

[5] 许棠.生物组织中的光传输及生物组织光学特性参数测量的研究[D].天津:南开大学,2004.

[6] HENON S,MEUNIER J.Microscope at the Brewster angle:Direct observation of first-order phase transitions in monolayers[J].Review of scientific instruments,1991,62(4):936-939.

[7] 王家礼,朱满座,路宏敏.电磁场与电磁波[M].西安:西安电子科技大学出版社,2008:193.

[8] 宫彦军,王喜昌,宋东草.折射定律与反射定律的推导[J].物理实验,2005,25(2):41-43.