关于起伏地表偏移表层高频校正量计算方法的讨论

林伯香,朱海波,徐 颖

(中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

在地表高程起伏变化大的山地地震资料处理中,起伏地表偏移是一个重要的处理环节。相对于水平基准面偏移,起伏地表偏移可以减少或消除具有地表一致性特点的静校正对波场特征的扭曲,提高成像精度[1-4]。在准确速度已知的理想情况下,非水平地表条件下的叠前偏移可以较圆满地解决复杂地表条件下的复杂构造成像问题[5],即在已知准确近地表速度时,起伏地表偏移本不存在表层静校正问题。但是,由于现有速度分析(或反演)技术的局限,起伏地表偏移过程中还需要使用静校正技术对近地表影响进行适当的校正,也就是所谓两步法起伏地表偏移[6-11]中的第一步——近地表校正。起伏地表偏移中的近地表校正与常规处理中的静校正[12-15]既有差异又有联系。如何在起伏地表偏移过程中实施有效的近地表校正,以抑制或消除地形与低速带变化对成像的不利影响,是业界面对的现实问题。

当前起伏地表偏移的近地表校正思路大致有2类。第1类是选择一个光滑基准面,利用静校正方法将炮点和接收点校正到该基准面以消除道间高频时差,该基准面也是后续叠前偏移成像和速度建模的参考面,中、低频道间时差的消除留给后续的速度建模解决[5,7-8]。王华忠等[5,7]提出该基准面作为消除高频道间时差的标准要尽可能接近地表;刘少勇等[8]通过平滑实际地表高程以获得该基准面。第2类是对已经校正到最终基准面的预处理地震数据应用反向高程静校正量以消除高程静校正量的影响,保留其余静校正量,以时间校正方式抑制近地表速度横向变化对成像的不利影响,但不改变炮点和接收点高程;以最大偏移孔径为半径平滑地表高程,作为叠前偏移成像和速度建模的参考面[9-11]。

林伯香等[15]以直射线Kirchhoff叠前时间偏移为例,研究了静校正中的高程校正部分所引起的误差,认为应该结合叠前偏移算法与速度分析技术本身对近地表速度横向变化的处理能力选择合适的近地表校正方式,但要尽可能避免采用导致改变炮点、接收点高程的静校正部分。

“面向起伏地表偏移成像的表层静校正方法”一文[6](以下简称文献[6])是对上述第1类近地表校正思路的具体实现方式的尝试。该文遵循“由于方法存在误差,静校正无法正确校正低频分量,因此在两步法起伏地表偏移成像中,静校正只适用于校正高频分量,低频校正量应由后续的偏移速度分析完成”的基本思路,提出了只校正高频校正量的表层静校正方法和相应的高频静校正量和高频基准面确定方法,试图找出一种在缺乏精确的全深度

速度模型情况下进行起伏地表偏移的表层静校正方法。我们以为,高、低频静校正量分解的思路应该是正确的,高频静校正分量用以补偿建模精度的不足；但文献[6]对应用高频静校正量后表层对数据影响的认识存在偏差,在存在明显低速带时,这种认识偏差将导致处理结果误差,低速带越厚速度越低误差越严重。

我们针对文献[6]的高频静校正、高频基准面计算方法展开讨论。在引述文献[6]基本论点的基础上,结合一个简单的模型说明这种高频静校正方法存在的不足,阐述了这种高频静校正量应用后表层对数据的影响,给出了针对第1类近地表校正思路的计算高频静校正量和高频基准面的建议。

1 文献[6]的基本论点

高频静校正量是从常规静校正量中提取出的波数大于某一给定“高频阈值”(如0.5×10-3/m)的分量ΔT。在假设低速带底界与最终基准面比较平缓的条件下,高频静校正量主要来自地表起伏和表层速度突变两部分。对应的高频基准面高程Ed为

(1)

式中:Eb为平缓的底界高程;v为替换速度(一般为底界速度);T0为恒负的下剥静校正量;ΔT为高频静校正量。由于ΔT的绝对值一般较小,T0一般为绝对值较大的恒负量,所以公式(1)中的条件ΔT≥T0一般可以得到满足。

当存在低速带时,高频基准面高于地表面,如图1(文献[6]中的图4)中的红线所示。低速带越厚、速度越低,即T0的绝对值越大,高频基准面高于地表面越多。

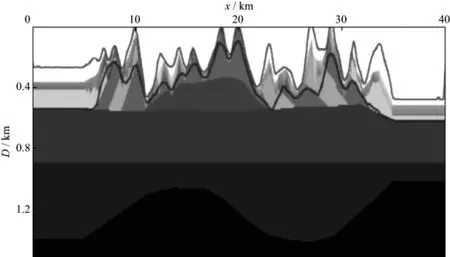
图1 阈值0.5对应的高频基准面(红线)[6]

不同静校正量计算方法,只要提取静校正量时用到了起伏地表和表层速度,得到的静校正量就包含了相同的、正确的高频成分,但它们的低频成分有所差异,而这部分低频成分恰恰是静校正的主要误差之所在。

理论模型试算中,在对数据应用高频静校正量并将炮点、接收点校正到高频基准面后,成像采用的速度模型在低速带底界之下为真实速度,在底界与高频基准面之间为填充速度。采用这样的偏移速度场是由于缺乏起伏地表速度分析的技术和手段。

用理论模型与实际资料,证实了该高频静校正方法及对应的高频基准面在“两步法”起伏地表偏移中是行之有效的。

2 针对文献[6]有关论点的讨论

文献[6]的高频基准面就是起伏地表偏移第1类近地表校正思路中的平滑基准面。我们以为,按公式(1)计算高频基准面并应用于起伏地表偏移成像,存在较大误差。下面从3个方面展开讨论。

2.1 炮点和接收点高程的改变实现了静校正低频分量的应用

将高频静校正量放在公式(1)的左边,公式(1)可写为公式(2)的形式。

(2)

对文献[6]给出的公式(1)可以这样理解,当对地震道的炮点或接收点应用高频校正量ΔT后,该地震道的炮点或接收点被校正到Ed面上(即所谓的高频基准面)。也就是说,当以Ed为基准面时,按常规静校正计算方法,即通过剥离低速带(公式(2)等号右边第1项),并在低速带底界与基准面之间填充替换速度(公式(2)等号右边第2项),计算的静校正量就是ΔT。当对数据应用高频静校正量ΔT后,就实现了地震数据到基准面Ed的全部静校正过程。

可见,文献[6]应用高频静校正量并校正到高频基准面后,应用了低速带的完整剥离量与从低速带底界到基准面的填充量。特别之处只是这里的基准面Ed是按公式(1)计算的与低速带剥离量T0、高频静校正量ΔT(依赖高频静校正量提取方法)等有关的可变量,而不是用户根据工区高程等情况给出的固定值。

采用相同的平滑步长对等式(1)两端的数据分别进行平滑,当平滑步长等于提取ΔT所使用的波数“高频阈值”的倒数(如0.5×10-3/m的倒数2000m)时,将得到

(3)

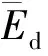
具有地表一致性特点的剥离与填充过程是静校正的核心,对地震数据的静态时移和对炮点、接收点高程的改变都是地表一致性静校正的实现方式。文献[6]看似仅对地震数据使用高频静校正量(静态时移),但却通过对炮点和接收点高程的包含低频成分的改变实现了对静校正低频分量的应用,不符合仅使用高频静校正量的初衷。

静校正的“地表一致性”仅仅是一种近似,现实中普遍存在远离“地表一致性”特点的情况。静校正中的剥离与填充所具有的地表一致性特点是“静校正无法正确校正低频分量”的本质原因,引入起伏地表偏移的目的就是要最大程度地避免使用具有地表一致性特点的静校正。

2.2 将文献[6]方法应用于简单模型存在问题

用水平地表、水平反射面和均匀低速带的一个简单模型(图2)加以说明,该简单模型可以被理解为是复杂近地表条件下一条地震测线的一部分。对于适合复杂近地表地震测线资料起伏地表偏移的静校正方法来说,首先必须适合这种简单的模型。

由图2可见,简单模型的水平地表面高程为0;横向均匀的低速层厚度200m,速度800m/s;低速层之下的水平高速层厚度1000m,速度2000m/s;对应的地下水平反射面埋深1200m。炮点和接收点布置在水平地表面上。

该简单模型符合文献[6]所指出的“T0一般为绝对值较大的恒负量”的条件。如此设计模型主要有两个目的:一是简单,通过简单计算而不必经过实际偏移处理过程即可得出明确结果;二是低速带较厚,使问题表现得更明显。

图3中的曲线L1是对简单模型以道间距20m,最大偏移距1000m正演模拟的CMP道集的水平反射面反射时距曲线,顶点在t=1500ms。使时距曲线最佳拉平的动校正速度(叠加速度)是1703m/s,对应的时距曲线是图3中的L2曲线。L2与L1基本重合,仅在远偏移距有些微可觉察的偏差。模型水平反射面以上的均方根速度是1697m/s。

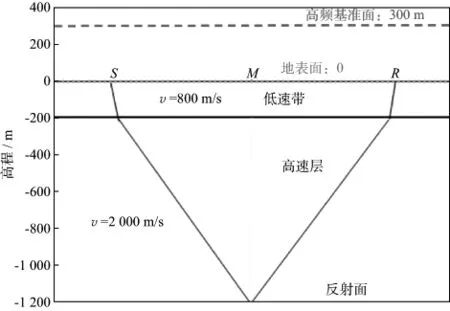
图2 具有水平地表、水平反射面和横向均匀低速带的简单模型

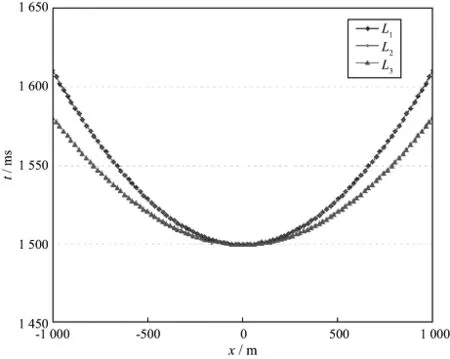
图3 简单模型正演CMP道集的水平反射面时距曲线

显然,针对该简单模型,低速带的下剥静校正量T0=-250ms,替换速度应该用2000m/s。无论如何选择文献[6]所述的提取高频静校正量的波数“高频阈值”参数,提取的高频静校正量均为0。按照文献[6]的公式(1)计算的高频基准面高程是300m。也就是说,在对来自这样简单模型的地震数据应用0高频静校正量(也就是不对地震数据做任何静态时移)的情况下,炮点和接收点被从高程为0的地表面校正到高程300m的所谓高频基准面上。这一点显然存在问题,问题就出在计算高频基准面的公式(1)包含了低速带的完整剥离量与从低速带底界到高频基准面的填充量。看似高频静校正量为0,实际上使用了具有地表一致性特点的静校正的剥离与填充技术改变了炮点和接收点的高程,也就是通过对炮点和接收点高程的包含低频成分的改变实现了对静校正低频分量的应用。

现在用该简单模型的正演CMP道集来分析偏移结果。根据公式(1),应用0高频静校正量后炮点、接收点被校正到高程300m的高频基准面上。用如下3种偏移速度处理方式,分析将会得到怎样的结果。

第1种方式,在(剥离)底界之下为真实速度,在底界与高频基准面之间为填充速度。这样,反射面与高频基准面之间将被看成均匀的介质进行偏移,即利用高速层的速度(2000m/s)对数据进行叠前深度偏移。反射面到高频基准面之间填充2000m/s速度时的反射时距曲线应该是如图3中的L3曲线(深度1500m,速度2000m/s的水平反射面时距曲线),与实际反射时距曲线L1有较大的差异。对于这种均匀水平单层模型,叠加与叠前偏移应该基本等效,能够使CMP道集同相叠加的叠加速度,也就是能够使叠前偏移成像道集同相叠加的速度。2000m/s的偏移速度偏大,无法使偏移的成像道集达到同相叠加,偏移结果无法得到比较清晰的反射界面的像。在信号主频不是很高时也许能得到模糊的像,且像出现的深度会大于实际反射面的深度。

可见,在底界与高频基准面之间采用填充速度难以使偏移结果清晰成像,应该通过速度分析得到合适的成像速度。文献[6]由于“缺乏起伏地表速度分析的技术和手段”,模型对比试算时采用了这种速度处理方式,削弱了对比结果的说服力。所给出的图4(文献[6]中的图6a)被认为是效果相对较好的,但总体上像的清晰度不高且横向上有变化,低速带较薄区域像的质量好一些,低速带厚的地方(高频基准面高于地面更多)像就模糊。

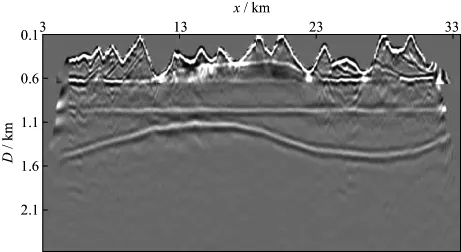
图4 阈值0.5高频基准面“两步法”起伏地表深度偏移成像结果[6]

第2种方式,以叠加速度1703m/s为成像速度。尽管炮点和接收点被校正到高程300m的高频基准面上,但由于对数据进行静态时移的高频静校正量为0,地震数据反射波时距关系并没有变化。成像道集的速度分析自然得到1703m/s的成像速度,用于偏移就可以得到清晰的反射界面的像,但反射界面将出现在地表面下977m(而不是1200m)处。因为地表面下977m位置相对300m高频基准面的深度是1277m,该深度水平反射面在上覆地层速度为1703m/s时的时距曲线就是L2线。这是仅考虑地面下1200m反射面的反射信号,而忽略低速带底界反射信号的速度分析和成像的情形。

第3种方式,如果在偏移和成像道集速度分析过程中还同时考虑了低速带底界的反射信号,应该能得到与理论模型一样的速度模型和成像结果。只是结果是相对高程300m的所谓高频基准面,而不是高程为0的地表面,结果整体上移了300m,即地表面下200m深度的低速带底界面成像在地表面之上100m处,地表面下深度1200m的反射面成像在地表面下深度900m处。

综上所述,对简单模型正演数据应用0高频静校正量并将炮点与接收点校正到300m的所谓高频基准面上后,叠前深度偏移无法得到一个清晰且正确的像。

2.3 高频静校正后表层对数据的影响

既然高频静校正量“来自起伏地表与表层速度的突变两部分[6]”,那么应用高频静校正量后,仅仅消除了地表起伏与表层速度突变部分对地震数据的影响,起伏地表与表层速度影响的中、低频分量还在,以某种等效表层的方式存在。高频基准面应该是这种等效表层的地形,且应该是实际地形的某种平滑结果;等效表层的速度,也应该是实际表层速度的某种平滑结果;只是等效表层的地形不像实际地形那么崎岖不平,等效表层速度也不像实际表层速度那样剧烈变化。表层速度与地形变化影响的中、低频分量,即等效表层引起的中、低频道间时差的消除将被融入到后续的速度估计、建模及叠前深度偏移过程中进行[5,7]。

对图2模型数据应用0高频静校正后,所谓的高频基准面还应该在高程为0的地表面上,低速带的影响还完完全全地存在,等效表层的地形还是原始的地形,等效表层的速度还是原始低速带的速度。当高频基准面为高程为0的地表面时,2.2节中“第3种方式”的结果就是正确的。

3 高频静校正量计算思路的建议

由(1)式计算的高频基准面总体趋势上大于地表高程,与实际地表高程间的差异含有明显的低频成分,不是实际地形的某种平滑结果。

高频静校正量是地形、低速带速度等因素变化共同作用产生的时间影响的高频部分。在文献[6]中,只要选好波数的“高频阈值”参数,计算高频静校正量是容易的。但是,要从已知的高频静校正量反推出正确的高频基准面(即等效表层的地形)却不容易,需要从一个时间值同时反推出地表高程与表层速度等参数的改变量。

我们建议,在选好波数的“高频阈值”参数后,分别对地表高程和近地表速度进行平滑滤波,得到平滑基准面和平滑低速带,再计算高频静校正量。这样剥离和填充可分解成2个方面,且都是高频的:一是低速带的剥离与填充,即剥离实际低速带、填充平滑低速带,校正实际低速带与平滑低速带之间的差异;二是地形的剥离与填充,校正实际地形与平滑基准面之间的差异。

以二维测线为例,设地形和近地表速度函数分别为e(x)和v(x),平滑滤波后分别是E(x)与V(x),又设低速带厚度为h(x)且低速带底界平滑。那么,用E(x)与V(x)替换e(x)和v(x)所产生的高频静校正量为

(4)

(4)式计算的ΔT与替换速度无关,仅“来自起伏地表与表层速度的突变两部分[6]”。应用ΔT后,对地震数据的时移量和对炮点、接收点高程的改变量(E(x)-e(x))自然都是高频的,低速带影响的低频分量(低速带底界面与平滑基准面E(x)之间速度为V(x)的低速带)留待后续的速度建模与偏移处理,符合起伏地表偏移第1类近地表校正思路的要求。

4 结束语

地震数据的静态时移和对炮点、接收点高程的改变都是静校正的表现形式。应用高频静校正量后的所谓高频基准面应该是地表高程的某种平滑结果,近地表(低速带、地形)影响的中、低频分量还在。如何在起伏地表偏移中计算与应用高频静校正量,取决于建模技术所得到的近地表与浅层速度模型的精度,以及叠前偏移算法对地形与近地表速度横向变化的处理能力,以时间校正的方式补偿速度精度的不足和偏移算法无法处理的近地表变化部分。先确定平滑基准面和平滑低速带,再计算高频静校正量,能够保证起伏地表偏移前仅使用静校正的高频分量。

参 考 文 献

[1] Wiggins J W.Kirchhoff integral extrapolation and migration of nonplanar data[J].Geophysics,1984,49(8):1239-1248

[2] Gray S,Marfurt K J.Migration from topography:improving the near-surface image[J].Canadian Journal of Exploration Geophysics,1995,31(1):18-24

[3] Li J C,Pham D.Land data migration from rugged topography[J].Expanded Abstracts of 72ndAnnual Internat SEG Mtg,2002,1137-1139

[4] 朱海波,张兵.起伏地表叠前时间偏移技术研究[J].勘探地球物理进展,2007,30(5):368-373

Zhu H B,Zhang B.Pre-stack time migration from topography[J].Progress in Exploration Geophysics,2007,30(5):368-373

[5] 王华忠,张兵,刘少勇,等.山前带地震数据成像处理流程探讨[J].石油物探,2012,51(6):574-583

Wang H Z,Zhang B,Liu S Y, et al.Discussion on the imaging processing workflow for foothill seismic data[J].Geophysical Prospecting for Petroleum,2012,51(6):574-583

[6] 刘玉柱,程玖兵,董良国.面向起伏地表偏移成像的表层静校正方法[J].石油物探,2012,51(6):584-589

Liu Y Z,Cheng J B,Dong L G.A new static correction method for the migration from rugged topography[J].Geophysical Prospecting for Petroleum,2012,51(6):584-589

[7] 王华忠,蔡杰雄,刘少勇.非水平地表情况下的叠前地震数据偏移处理方法与技术[C]∥赵殿栋.复杂山前带地震勘探技术研讨会文集.北京:地质出版社,2010:165-178

Wang H Z,Cai J X,Liu S Y.Prestack migration of the seismic data on topography[C]∥Zhao D D.Seismic techniques on complex foothill exploration.Beijing:Geology Press,2010:165-178

[8] 刘少勇,王华忠,张兵.起伏地表Kirchhoff积分法叠前深度偏移方法研究与应用[J].岩性油气藏,2010,22(F07):49-54

Liu S Y,Wang H Z,Zhang B.Kirchhoff integral PSDM for rugged topography:technology and applications[J].Lithologic Reservoirs,2010,22(F07):49-54

[9] 刘国峰,刘洪,李博,等.起伏地表直接叠前时间偏移[J].石油地球物理勘探,2010,45(2):196-200

Liu G F,Liu H,Li B,et al.Direct pre-stack time migration on rugged topography[J].Oil Geophysical Prospecting,2010,45(2):196-200

[10] 刘国峰,刘洪,李博,等.地震资料叠前时间偏移方法及其GPU实现[J].地球物理学报,2009,52(12):3101-3108

Liu G F,Liu H,Li B,et al.Method of prestack time migration of seismic data of mountain regions and its GPU implementation[J].Chinese Journal of Geophysics,2009,52(12):3101-3108

[11] 朱海波,林伯香,徐兆涛,等.起伏地表叠前时间偏移处理流程及其应用研究[J].石油物探,2012,51(5):486-492

Zhu H B,Lin B X,Xu Z T,et al.Prestack time migration from rugged topography and its application[J].Geophysical Prospecting for Petroleum,2012,51(5):486-492

[12] 李录明,罗省贤.复杂三维表层模型层析反演和静校正[J].石油地球物理勘探,2003,38(6):636-641

Li L M,Luo X X.Tomographic inversion for 3D complex near-surface model and static correction[J].Oil Geophysical Prospecting,2003,38(6):636-641

[13] 王彦春,余钦范,李峰,等.交互迭代静校正方法[J].石油物探,1998,37(2):63-70

Wang Y C,Yu Q F,Li F,et al.The method of static correction by interactive iteration[J].Geophysical Prospecting for Petroleum,1998,37(2):63-70

[14] 林伯香.最小静校正误差浮动基准面方法[J].石油地球物理勘探,2003,38(6):611-617

Lin B X.A new method for determination of floating datum in static corrections[J].Oil Geophysical Prospecting,2003,38(6):611-617

[15] 林伯香,朱海波,虞立,等.静校正对叠前时间偏移的副作用[J].石油地球物理勘探,2013,48(2):214-221

Lin B X,Zhu H B,Yu L,et al.Side-effects of static corrections to prestack time migration[J].Oil Geophysical Prospecting,2013,48(2):214-221