钢斜拉桥的稳定性评估

于德安, 檀永刚, 张 哲

(大连理工大学 桥梁工程研究所, 辽宁 大连 116023)

斜拉桥近年来在世界各地非常流行,因为它为中、大跨度桥梁提供一个经济的解决方案,结构受力合理,外形美观[1].世界各地已经建成许多中等和大跨度斜拉桥梁,特别是亚洲.中国的苏通大桥,其主跨跨径达到1 088 m,是世界第二大跨径的斜拉桥.还有日本的多多罗大桥和俄罗斯的跨东博斯普鲁斯海峡的俄罗斯岛大桥.斜拉桥有三个主要组件,主缆、梁和塔.主缆必须承受主梁传来的载荷,梁和塔必须抵抗弯矩以及轴向压力.尤其是钢桥塔,由于钢桥塔长细比比较大,钢板厚度比混凝土塔壁薄,所以钢桥塔更容易发生失稳.钢主梁同样存在这样的问题.因此梁和塔的稳定计算非常重要.

稳定问题是桥梁工程中经常遇到的问题,与强度问题有着同等重要的意义.历史上由于对其缺乏足够的认识,出现过不少桥梁失稳的事故.在我国设计规范中,主要要求对塔、梁分别进行稳定性计算,稳定安全系数不小于4.这种简化计算并不是最经济的方法.因此,斜拉桥主要受力构件精确的稳定计算,对评估钢斜拉桥的经济性和安全性具有特别重要的意义.

稳定性的定义为:结构在载荷作用下处于平衡位置,微小外界扰动使其偏离平衡位置,当扰动消除后仍能回复到初始平衡位置,则称为是稳定平衡状态.若扰动消除后不能恢复到初始平衡位置,而在新的状态下平衡,则原来的平衡状态就称为不稳定平衡状态.结构的失稳问题分为三类:分枝点失稳、极值点失稳和跳跃失稳.真实的工程问题都属于第二类失稳状态,即极值点失稳.

1 受力构件的稳定评价方法

1.1 ASD理论的轴向弯曲交互作用公式

ASD中验算钢斜拉桥主要受力构件稳定性的轴向弯曲交互方程表达式[2]如下:

(1)

式中:fc为最大轴向压应力;fb y为y轴弯矩计算的最大应力;fb z为z轴弯矩计算的最大应力;Fe y为y轴许用欧拉屈曲应力;Fe z为z轴的许用欧拉屈曲应力;Fb y和Fb z分别为y轴和z轴的许用弯曲应力;Fa为许用压应力,表达式如下:

(2)

式中:Fc r为屈曲应力;FS为安全系数,其值为2.12.另外,考虑二阶弯矩效应,可取力矩放大系数为1/(1-fc/FE).

1.2 LRFD理论的轴向弯曲交互作用公式

LRFD中验算钢斜拉桥主要受力构件稳定性的轴向弯曲交互方程表达式[3]如下:

(3)

(4)

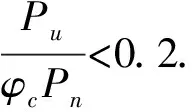
式中:Pu、Muy、Muz分别为轴向力、y轴弯矩和z轴弯矩;φc和φf分别为轴向力和弯矩的强度折减系数;Mny和Mnz为y轴和z轴的名义弯矩;Pn为名义轴力,表达式为Pn=FcrA.在LRFD理论中,二阶矩效应分成两类:P-δ效应(无侧移情况)和P-Δ效应(有侧移情况).通常,二阶矩效应的表达式为:

Mu=B1Mnt+B2Mlt,

(5)

式中,Mnt和Mlt分别为无侧移弯矩和有侧移情况下的弯矩;B1和B2分别为无侧移和有侧移情况下的力矩放大系数,其表达式如下:

(6)

式中:Pu1为无侧移情况下的轴向力;Pe1为无侧移情况下的欧拉屈曲载荷;Pu2为有侧移情况下的轴向力;Pe2为有侧移情况下的欧拉屈曲载荷.

2 两种屈曲分析理论

2.1 特征值屈曲分析

特征值屈曲分析用于预测一个理想弹性结构的理论屈曲强度,其计算方程[4]为

([KE]+λi[KG]){φi}=0.

(7)

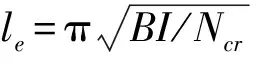
2.2 非线性屈曲分析

非线性屈曲分析是通过逐渐增加载荷来求得使结构开始变得不稳定时的非线性静力分析技术.近似的非线性求解是将载荷分成一系列的载荷增量,在每一个增量求解完成后,进行下一个载荷增量之前,程序调整结构的刚度矩阵以反映结构刚度的非线性变化.通常有载荷增量法、牛顿-拉夫逊法及弧长法等.在弧长法中,非线性方程[5]为

(8)

式中:i为迭代次数;Δλi+1为载荷增量步长系数;{ΔR}为第i次迭代的不平衡力;位移增量{Δδ}i+1分为两部分:

(9)

3 研究对象及计算模型

3.1 工程概况及计算模型

某座正在设计的单塔斜拉桥,跨径为180 m,桥梁宽度为28 m,钢桥塔高度128 m,立面图如图1所示.

利用ANSYS建立模型,ANSYS是一款通用有限元软件,在分析过程中可根据不同的特点和分析目的用不同的单元来模拟不同结构[6].桥塔及主梁用BEAM4单元,拉索采用LINK10单元,采用命令流建模方式,考虑静力载荷作用,按弹性屈曲理论分析,部分命令流如下:

FINISH

/CLEAR

/PREP7

/UNIT,SI

ET,1,BEAM4

ET,2,LINK10!定义单元

……

/SOLU

ANTYPE,0 !设定求解类型

EQSLV,SPAR

PSTRES,ON !打开预应力选项

……

ANTYPE,1

BUCOPT,LANB,1,0,0 !指定屈曲分析

MXPAND,1,0,0,1,0.001! 模态扩展分析

……

FINISH

有限元模型如图2.

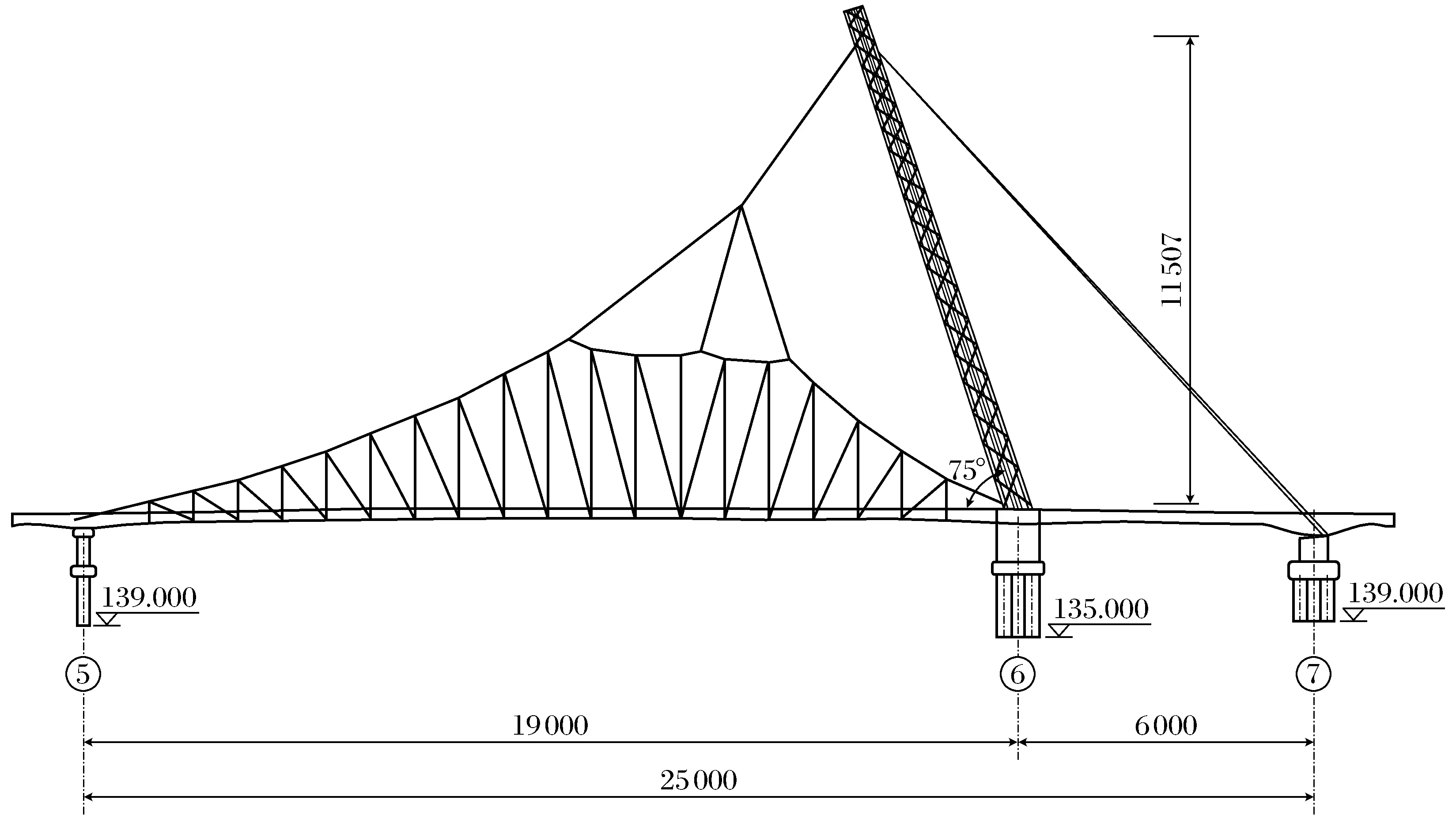
图1 全桥立面图(单位: cm)Fig.1 The vertical view of the whole bridge(Unit: cm)

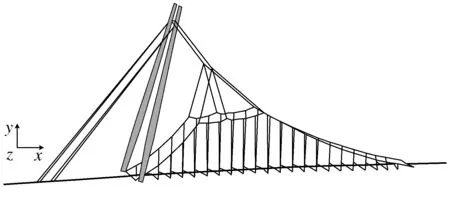
图2 有限元模型Fig.2 Finite element model

3.2 计算结果及分析

(1) 计算出各构件的轴力及弯矩,利用稳定交互公式进行计算,然后对结果进行计算统计.得到结果如图3,其中纵坐标为稳定性计算值,对应于公式(1)、式(3)、式(4)的左边项;横坐标为主梁及主塔的位置坐标,单位为m.

通过图3比较可以看出,LRFD理论计算值普遍小于ASD理论计算值,通过公式(1),式(3),

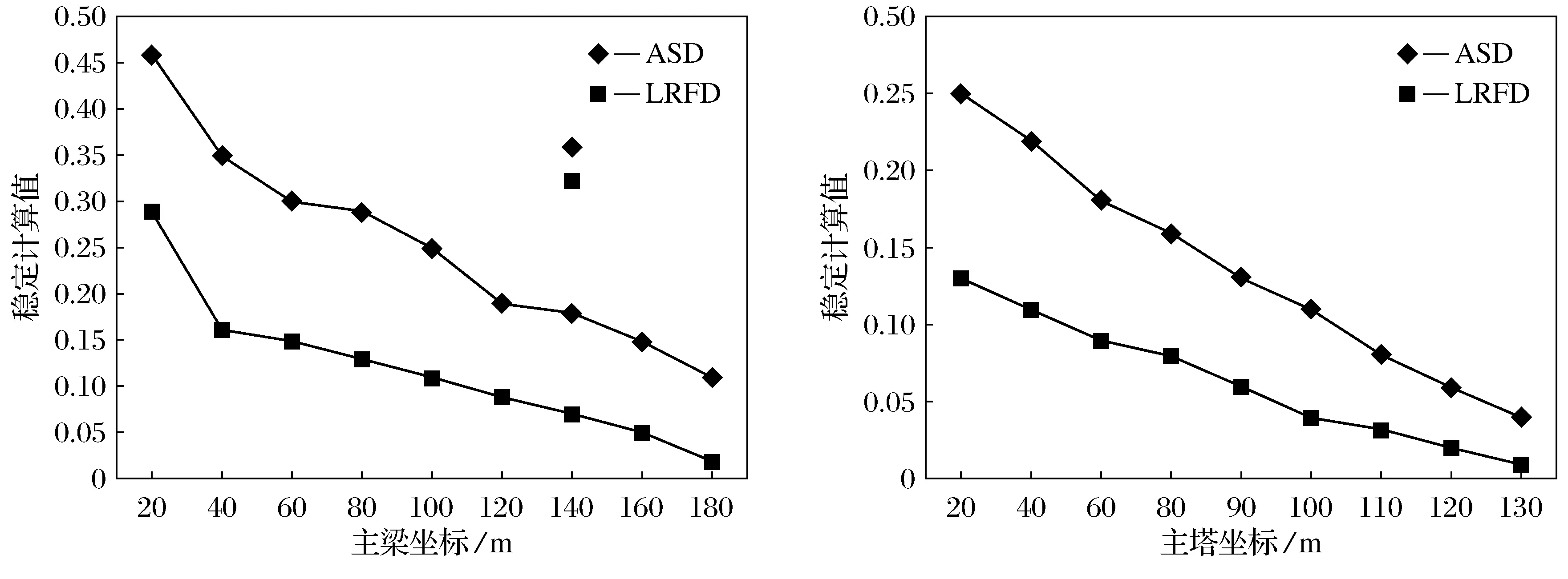
图3 稳定计算值统计Fig.3 Statistics of stability calculation value

式(4)可以看出,稳定计算值越小,则表明轴向弯曲交互作用造成的不稳定影响越低,即该种情况下结构稳定性越好.在梁柱交叉点的位置表现最明显,而远离交叉点位置后差距变小,并且逐渐趋于稳定.通过分析可知,在静力和弹性条件下,LRFD理论计算的稳定性值比ASD理论计算的稳定性值低15%～20%,因此,在条件允许情况下,推荐使用LRFD理论进行轴向弯曲交互作用的稳定分析.

(2) 利用ANSYS有限元程序进行静力分析可得到主要受力构件的受力情况,计算出钢塔的等效载荷为690 t,然后进行弹性屈曲分析(即特征值屈曲分析),在ANSYS中主要是用BUCKLE分析得以实现,通过计算可以从程序中得出钢塔的弹性屈曲系数见表1.

如前文所述,则该结构可承受的屈曲载荷为6.73×690 t=4 375 t,该数值表明塔结构在6.73倍等效载荷的作用下会发生第一类失稳破坏.

表1 钢塔弹性屈曲系数Table 1 Elastic bulking coefficient of the steel tower

然而,由于工程材料的初始缺陷和施工误差,实际工程中的问题通常表现为第二类失稳破坏,所以,只计算第一类稳定不能准确衡量构件的稳定性,第一类稳定破坏的临界载荷值只是理论解.真实的破坏载荷通常都是低于第一类稳定破坏的载荷,多数情况下表现为非线性的破坏,因此,为比较一类稳定和二类稳定之间的差距大小,本文用ANSYS程序进行非线性弹性分析.在进行非线性弹性分析时,主要考虑几何非线性和材料非线性,即双重非线性.在模型中,几何非线性主要通过施加初始几何缺陷的方法实现,即提取计算第一类稳定时的一阶模态的变形,按照实际构件尺寸1%的比例施加在非线性计算的模型上.而材料非线性则主要通过定义材料的非线性本构关系,在该计算模型中,由于钢塔采用的是Q345的钢材,则定义屈服强度为345 MPa,切线模量为0.79 GPa,赋予方式采用ANSYS中BKIN的双线性随动强化模型.考虑到计算结果的精度和收敛性,该模型计算时,采用弧长法计算,通过调整弧长半径和子步数,使结果达到一个相对满意的解.而载荷的施加则是取一类稳定的临界载荷值乘以1.15的放大系数,以确保结构能够发生第二类失稳.计算结果可通过时间后处理器,即POST26查看,结果见图4,其中纵坐标为加载的载荷值(kt),横坐标为塔顶的位移值(m).

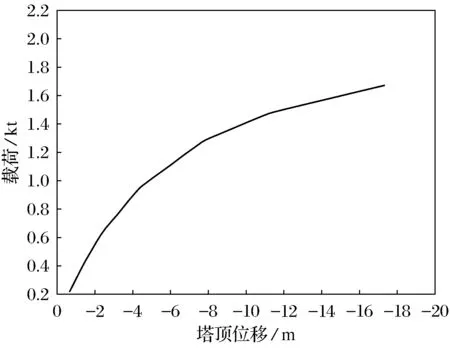
图4 载荷曲线Fig.4 Load curve

当曲线到达峰值时,可得屈曲载荷为2×1 670 t=3 340 t,在该种情况下,钢塔杆件的应力达到屈服载荷强度,开始塑性变形,变形增长很快,承载力增加缓慢,可以认为达到了极限承载力状态.与弹性分析相比,非线性弹性分析的屈曲载荷降低了24%左右,即非弹性屈曲计算的结果更接近真实情况,并且承载能力降低较多.

4 结 论

通过对比计算结果可以得出以下结论:

(1) 在梁柱交叉位置稳定计算值比较大,并且ASD与LRFD的结果相差较大,远离交叉点后计算值都变小,并且LRFD比ASD节省的效果逐渐弱化.当达到一定距离之后,这种节省效果趋于稳定,并保持在一个具体的数值附近.

(2) 在静力以及弹性条件下,LRFD理论计算的稳定性值比ASD理论计算的稳定性值低15%～20%,即采用LRFD设计比ASD设计可以节约15%～20%.

(3) 通过该工程实例的计算,非线性屈曲载荷比弹性屈曲载荷低24%左右,二者结果差距较大,所以在工程设计时应该计算非线性屈曲载荷,从而使设计更安全.

参考文献:

[1]Gimsing N J, Georgakis C T. Cable-Supported Bridges: Concept and Design[M]. Hoboken, N J: Wiley, 1983).

[2]AASHTO. AASHTO LRFD Bridge Design Specifications[S]. 3rd ed, 2004.

[3]AASHTO. AASHTO Standard Specifications for Highway Bridges[S]. 16th ed, 1996.

[4]王新敏. ANSYS工程结构数值分析[M]. 北京:人民交通出版社, 2007:410-414.

(Wang Xinmin. Numerical Analysis of ANSYS Engineering Structure[M]. Beijing: China Communication Press, 2007:410-414.)

[5]王星海. 独塔斜拉桥的整体稳定性分析[D]. 长沙:长沙理工大学, 2007:35-36.

(Wang Xinghai. The Whole Stability Analysis of the Cable-Stayed Bridge with Single Tower[D]. Changsha: Changsha University of Science & Technology, 2007:35-36.)

[6]王超,檀永刚,韩义乐. 基于ANSYS与SiPESC.OPT的自锚式悬索桥合理成桥索力优化[J]. 沈阳大学学报:自然科学版, 2013,25(6):506-509

(Wang Chao,Tan Yonggang,Han Yile. Optimization of Rational Bridging Cable Force of Self-Anchored Suspension Bridge Based on ANSYS and SiPESC. OPT[J]. Journal of Shenyang University: Natural Science, 2013,25(6):506-510.)