基于灰色预测GM(1,1)的企业利润预测

赵春阁, 徐 群

(兰州商学院 a. 信息工程学院, b. 工商管理学院, 甘肃 兰州 730020)

企业利润预测是一个企业生存和发展的重中之重.对未来利润的预测关系到一个企业的发展前景,是其现阶段如何组织收入、控制成本费用、评价经营成果的基础.它可以评价企业的可持续发展能力,是一个企业的“晴雨表”.灰色预测GM(1,1)[1]模型具有运算方便、建模精度高等特点,近年来被广泛应用于各种预测领域.

灰色预测模型的应用领域越来越广泛,赖红松等[2]等研究了基于灰色预测和神经网络的人口预测,用灰色预测和神经网络相结合的方法来对人口进行预测;魏义坤等[3]研究了多变量灰色模型在农作物单产预测中的应用,从单点灰色模型入手,通过扩展,导出多变量灰色模型,根据已知过去几年的数据建立灰色模型进行拟合和预测,为科学种田提供了依据;刘发全等[4]提出了灰色预测GM(1,1)模型的一点改进,讨论了灰色预测GM(1,1)模型理论中存在的一些问题,推导出了新的灰色预测公式,从而进一步提高了预测精度,并且通过实例验证了新的预测公式的正确性及可行性;赵爱文等[5]研究了中国碳排放的灰色预测,通过灰色GM(1,l)模型对中国碳排放进行了短期预测,并且针对研究结果提出了发展低碳经济、提高能源效率以及通过发展非化石能源来降低碳排放的策略;曲赜胜等[6]研究了辽宁省住宅产业碳排放量的灰色预测分析,运用灰色预测模型对2011—2020年辽宁省住宅产业碳排放量进行了预测,拟合值计算结果表明预测值与实际值的吻合程度符合预期结果,预测结果显示辽宁省住宅产业未来一段时期依然面临较大的碳减排压力;吉培荣等[7]研究了灰色预测模型的特性,对GM(1,1)模型的特性进行了研究,证明了GM(1,1)模型是有偏差的指数模型,分析了模型偏差的特性,进而从理论上阐明了GM(1,1)模型误差的实质;岑詠霆[8]研究了销量预测的改进型灰色预测GM(1,1)模型,在传统的灰色预测GM(1,1)模型中,以预测值与原始值的差方和最小为目标,对模型构建的背景值的设定中,令μ在[0,1]中以Δμ为增量扫描比较,以确定最佳的μ值,在模型求解中以同样的目标确定参数C的值,从而提高了预测精度.上述研究多为大层次方面的研究,如人口预测、碳排放预测、能源预测等,单纯地运用灰色预测,其精度还不够准确,所用的求解方法复杂.由于灰色模型的计算过程多为矩阵的计算,因此本文借用MATLAB软件在矩阵计算方面独有的优势,研究了日常生活中最常见的利润问题,它也是企业最注重的问题,利用灰色预测的实用性,将MATLAB和灰色模型相结合,实现了系统的预测,提高了计算的效率.

1 GM(1,1)模型基本原理

灰色预测通过鉴别系统因素之间发展趋势的相异程度,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律的数据序列,然后建立相应的微分方程模型,从而预测事物未来的发展趋势.灰色预测的数据是通过生成数据的模型所得到的预测值的逆处理结果.灰色预测是以灰色模型为基础的.在诸多的灰色模型中,灰色系统中单序列一阶线性模型GM(1,1)模型最为常用.下面介绍GM(1,1)模型的预备知识.

(1) 模型符号的含义如下:

(2) 生成数. 生成数分为累加生成数(AGO)与累减生成数(IAGO).

① 累加生成数. 1-AGO指一次累加生成.记原始序列为

x(0)=(x(0)(1),x(0)(2),…,x(0)(n)),

则生成序列为

x(1)=(x(1)(1),x(1)(2),…,x(1)(n)).

② 累减生成数.累减生成数是累加生成的逆运算.记原始序列为

x(1)=(x(1)(1),x(1)(2),…,x(1)(n)),

对x(1)作一次累减生成,则得如下生成序列:

x(0)=(x(0)(1),x(0)(2),…,x(0)(n)).

式中,x(0)(k)=x(1)(k)-x(1)(k-1). 规定x(1)(0)=0.

2 GM(1,1)模型

下面介绍GM(1,1)模型的功能实现.设有如下原始数据序列:

x(0)=(x(0)(1),x(0)(2),…,x(0)(n)).

式中,n为数据的个数.如果根据x(0)数据序列建立GM(1,1)模型来实现功能预测,那么基本步骤如下.

(1) 为了弱化随机序列的波动性和随机性,对原始数据进行累加,得到如下新数据序列:

x(1)=(x(1)(1),x(1)(2),…,x(1)(n)).

式中,x(1)(t)中各数据用来表示对应前几项数据的累加,即

(2) 对x(1)(t)建立x(1)(t)的一阶线性微分方程:

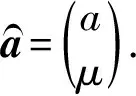
(3) 对累加生成数据作均值生成B与常数项向量Yn,即

Yn=(x(0)(2),x(0)(3),…,x(0)(n))T.

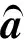
(7) 对建立的灰色矩阵进行检验.检验步骤如下:

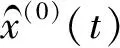
② 求原始数据x(0)的均值以及方差s1;

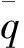
⑤ 求小误差概率P=P{|e(t)|<0.674 5s1};

⑥ 灰色模型精读检验对照表如表1所示;

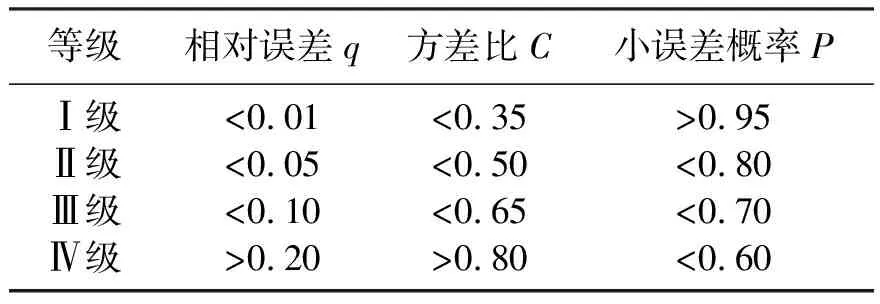
表1 灰色模型精读检验对照表Table 1 Grey model intensive examination table

⑦ 利用模型进行预测:

3 实例验证

由于灰色预测中有诸多关于矩阵的运算,MATLAB程序有较强的通用性,因此,用MATLAB是实现灰色预测的首选.用MATLAB编写灰色预测程序时,其步骤可以完全按照以上GM(1,1)模型的步骤,即①对原始数据进行累加;②构造累加矩阵B与常数项向量;③求解灰参数;④将参数代入预测模型进行数据预测.

实例对某公司的收入进行灰色预测.假设该公司2005—2014年的利润如表2所示,要求预测该公司未来几年的利润情况.

表2 某公司2005—2014年的利润Table 2 The profits of a company 2005—2014

编写MATLAB程序,观察其运行结果,如下:

G =1.0e+05*

Columns 1 through 10

Columns 11 through 20

同时,MATLAB程序还显示出了预测数据与原始数据的比较图,如图1所示.

图1 某公司利润预测数据与原始数据的比较

由MATLAB灰色预测数据和对比图可见,利用灰色预测模型预测的公司未来几年的利润与实际值吻合程度较高,由图1可以清晰明了地看出公司未来几年的利润一直呈上升状态,可以为该公司制订发展策略提供借鉴.

4 结 语

灰色预测具有适用性的优点,有严格的理论基础,其模型预测结果比较稳定,不仅适用于大数据的预测,在数据较少时预测结果依然很准确.MATLAB语言系统中,几乎所有的操作都是以矩阵操作为基础的,而在灰色模型预测过程中,有很多关于矩阵的运算,所以本文利用灰色预测与MATLAB相结合的方法,建立了GM(1,1)模型,并在MATLAB上很好地实现了模型的求解,证明了模型的有效性和适用性,并且可以为企业预测未来的利润以及制订发展计划提供参考和借鉴.

参考文献:

[1]邓聚龙. 灰色系统基本方法[M]. 武汉:华中理工大学出版社, 1987.

(Deng Julong. Basic Methods of Gray System[M]. Wuhan: Huazhong Institute of Technology Press, 1987.)

[2]赖红松,祝国瑞,董品杰. 基于灰色预测和神经网络的人口预测[J]. 经济地理, 2004,24(2):197-201.

(Lai Hongsong,Zhu Guorui,Dong Pinjie. Population Forecast Based on Combination of Gray Forecast and Artificial Neural Networks[J]. Economic Geography, 2004,24(2):197-201.)

[3]魏义坤,龚灏,任鹏,等. 多变量灰色模型在农作物单产预测中的应用[J]. 沈阳大学学报, 2008,20(6):107-109.

(Wei Yikun,Gong Hao,Ren Peng,et al. Application of Multi-variable Gray Model to Forecast of Per Unit Yield of Crops[J]. Journal of Shenyang University, 2008,20(6):107-109.)

[4]刘发全,职承杰. 灰色预测GM(1,1)模型的一点改进[J]. 数学的实践与认识, 2005,35(11):11-15.

(Liu Faquan,Zhi Chengjie. Improvement of Grey Prediction Model GM(1,1)[J]. Mathematics in Practice and Theory, 2005,35(11):11-15.)

[5]赵爱文,李东. 中国碳排放灰色预测[J]. 数学的实践与认识, 2012,42(4):61-69.

(Zhao Aiwen,Li Dong. Grey Forecast of China’s Carbon Dioxide Emissions[J]. Mathematics in Practice and Theory, 2012,42(4):61-69.)

[6]曲赜胜,李玲,张萌萌. 辽宁省住宅产业碳排放量的灰色预测分析[J]. 沈阳大学学报:社会科学版, 2013,15(2):143-146.

(Qu Zesheng,Li Ling,Zhang Mengmeng. Grey Prediction Analysis on Carbon Emissions in Housing Industry of Liaoning Province[J]. Journal of Shenyang University: Social Science, 2013,15(2):143-146.)

[7]吉培荣,黄巍松,胡翔勇. 灰色预测模型特性的研究[J]. 系统工程理论与实践, 2001(9):105-108,139.

(Ji Peirong, Huang Weisong,Hu Xiangyong. A Study on the Properties of Grey Forecasting Model[J]. Systems Engineering: Theory & Practice, 2001(9):105-108,139.)

[8]岑詠霆. 销量预测的改进型灰色预测GM(1,1)模型研究[J]. 工业工程与管理, 2013,18(1):37-40,45.

(Cen Yongting. The Research of Sales Forecasting’s Improved Grey Forecasting GM(1,1) Model[J]. Industrial Engineering and Management, 2013,18(1):37-40,45.)