四辊板带轧机厚度的模糊自整定PID控制
2014-03-26邓思聪樊立萍
邓思聪,樊立萍
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
金属板带材是钢铁冶金工业的重要产品,广泛应用于汽车制造、食品包装、家用电器、机械及其他一些领域[1].厚度是板带钢材最主要的质量指标之一,厚度自动控制是现代板带钢材生产中不可缺少的重要组成部分.厚度控制的目的就是通过调节辊缝、张力、电机速度等参数,消除轧制过程中影响厚度精度的因素,最终达到预先设定的厚度值.
轧机板厚控制系统是一个具有非线性、时滞性、时变性、大惯性、多变量耦合等特性的复杂系统.板带轧机板厚控制技术及其理论的发展经历了由粗到精由低到高的发展过程[2].传统的厚度控制系统一般采用经典的PID调节器来实现.常规PID控制具有原理简单、使用方便、适用性和鲁棒性好等优点.因此,被大量地应用于工业生产过程控制中.由于控制对象的复杂性,控制系统的精确数学模型无法建立,传统的PID控制因存在参数整定困难、控制品质欠佳等问题,已越来越不能满足控制要求[3-4].随着自动控制理论和计算机技术的发展及应用,板厚控制技术产生了重大变革.四辊轧机的板厚控制技术向着大型化、高速化、连续化的方向发展.
模糊控制技术是近代控制理论中的一种高级策略和新颖技术.模糊控制技术基于模糊数学理论,通过模拟人的近似推理和综合决策过程,使控制算法的可控性、适应性和合理性提高,成为智能控制技术的一个重要分支.模糊控制不需要被控对象的精确数学模型,而且具有较强的鲁棒性,尤其适合于非线性、时变及纯滞后系统的控制.但是,模糊控制的设计尚缺乏系统性,模糊规则及隶属函数的确定过分依赖专家经验.同时,由于常规模糊控制器只能实现有差调节,在控制精度要求较高的控制过程中,很难满足实际工业生产的要求.
将PID控制技术和模糊控制技术结合起来,取长补短,可以取得更好的控制效果.本文基于模糊PID的四辊轧机厚度控制,通过模糊控制器中的隶属度函数和模糊规则表,结合系统的误差和误差率在线调节PID参数.
1 四辊板带轧机厚度系统模型的建立
1.1 轧机轧制过程的基本原理
在两个具有刚性强度的工作辊之间,事先将辊缝大小设定为人们想要得到的厚度h,轧制之前的厚度为H,这样当钢板通过轧机的工作辊后,由于发生了塑性形变,钢板的厚度就变为h,从而得到所需厚度的产品.
1.2 四辊板带轧机厚度系统的厚度控制理论与控制方法
轧机的控制方式分为两种,分别是前馈控制和反馈控制.前馈控制的优点是事先测量来料的厚度,消除了时间上的滞后.但它的缺点是属于开环控制,不能将误差反馈回去,反馈控制又存在一定的滞后性.所以,本文采用的是前馈控制和反馈控制相结合的控制方式.前馈控制的主要作用是:由于来料的表面并不平整,需要在进口时测得来料的厚度变化,再把测得的数据传输到液压AGC系统,系统会根据接收到的数据大小,产生相应的轧制力.反馈控制的作用是:将出口处检测到的值反馈回去与设定值作差,得到一个误差值,再通过控制器将使误差变得越来越小.其中压下系统是轧机控制系统的核心.
1.3 四辊板带轧机厚度系统数学模型的建立
对于轧机厚度系统最重要的指标是产品的厚度精度.与厚度精度密切相关的模型有两个:轧制力计算模型和轧机弹跳模型.
1.3.1 轧制力计算模型
(1)
四辊板带轧机厚度系统的输出量为压下量Δh,该值可根据轧制力计算公式(西姆斯公式)[5]求得:
(2)
其中:F—轧制力的大小(kN);∂—平均变形抗力(MPa);W—轧件在轧制前后的平均宽度(mm);△h—压下量(mm);R′—弹性压扁的轧辊半径(mm);QP—轧制力函数.
公式(2)中的R′为弹性压扁半径.当工作辊与钢板接触时,由于相互挤压,工作辊会产生一定的弹性压扁,这样会导致轧辊与轧件的接触面积增大,使得轧件受到了一个更大的轧制力,影响轧件的精度.在计算弹性压扁时采用 Hitchcock 公式[6]:
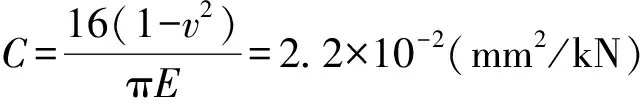
(3)
R0—轧辊初始半径;E—轧辊弹性模量;v—软件波松比.
1.3.2 轧制力函数计算模型
公式(1)中QP为轧制力函数.可通过轧制力函数公式求得[7]:
(4)
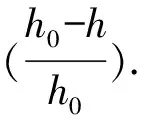
1.3.3 轧机弹跳模型
在轧钢过程中,由于轧机受到力的作用会发生弹性形变,同时轧件也会发生一定的塑性形变,这些都对精度产生了影响.轧件的出口厚度值根据厚度计算公式[8]求得,并代入公式(4)可求出轧制力函数.
厚度计算公式:
h=S+(SF-SF0)C+Δi
(5)
其中:S—初始设定辊缝(mm);SF—轧制力为F时的弹跳量(mm);SF0—预压靠时的弹跳量(mm);C—宽度补偿系数(mm);Δi—轧辊热膨胀和磨损补偿量(mm).
2 四辊板带轧机厚度系统模糊自整定PID控制器的设计
2.1 模糊自整定PID控制器的介绍
基于控制模型的模糊自整定PID控制如图1所示.PID控制器中的3个参数值不容易确定,因此,采用与模糊控制器相串联的控制方式.这种控制方式的优点在于对PID参数的初始设定值的准确性要求并不高,在PID参数不精确的情况下,通过对PID参数的动态整定也能达到良好的效果.模糊PID就是在PID控制的基础上,使用模糊控制理论进行优化.通过模糊规则来决定控制输出U的大小,模糊控制的作用主要起到将人的经验加到控制中去.通过仿真结果的对比,采用模糊PID控制比传统的PID控制具有稳定性更高,以及更加快速地达到稳态效果.

图1 模糊自整定PID原理
2.2 模糊自整定PID控制器的设计以及参数整定
(1) 选定模糊控制器采用双输入三输出方式,两个输入为误差(Ke)和误差率(Kec),三个输出为KU1、KU2、KU3.分别控制PID的kp、ki、kd三个参数.即kp=kp′±△kp、ki=ki′±△ki、kd=kd′±△kd
(2) 选定误差(Ke)、误差率(Kec)和输出(KU)的论域和分档.根据实际测量和专家经验把三者的论域分为[-6,6].根据设计需要,对它们分别模糊化,模糊变量E、EC和U的论域划分为:{-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6}.用语言变量来表示为:{NB,NM,NS,ZO,PS,PM,PB}
(3) 模糊规则表的设计.主要是根据专家经验和对现场实际工作过程的总结,但它也遵循一定的规律,即模糊控制规则编写的基本思想是:当误差(Ke)为负大时,若误差率(Kec)变化也为负大,这时说明偏差有增大的趋势,为了尽快消除己有的负大偏差并抑制偏差变大,则输出(KU)的变化取正大.其它情况的控制规则类似.模糊规则见表1~表3.

表1 △kp模糊规则

表2 △ki模糊规则
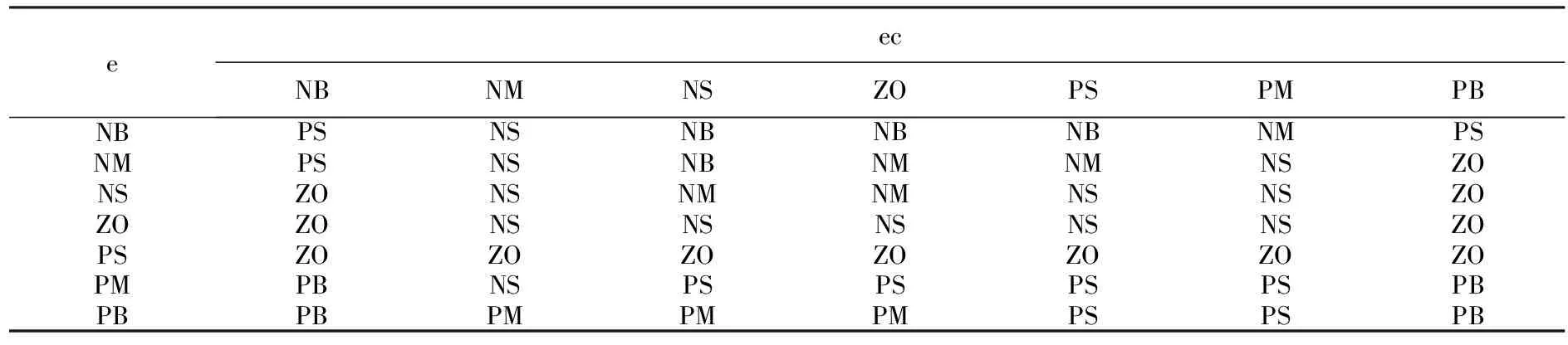
表3 △kd模糊规则
3 模型的建立及仿真结果
利用Matlab 软件的Simulink 工具箱建立控制系统的仿真实例.
3.1 仿真中用到的相关数据值
CP=109N/m、h0=5 mm、h=3 mm、R′=25 mm、W=2 000 mm、δ=15 MPa
PID参数的值设为P=25、I=20、D=1、Ke=1、Kec=0.01、KU1=25、KU2=20、KU3=10.
3.2 仿真模型及结果
根据以上的数学公式可以建立轧钢系统的仿真模型.仿真结果示于图2~图6.

图2 模糊自整定PID中△kp值的变化曲线

图3 模糊自整定PID中△ki值的变化曲线

图4 模糊自整定PID中△kd值的变化曲线

图5 模糊自整定PID 与经典PID 的误差曲线比较

图6 模糊自整定PID 与经典PID 的仿真曲线比较
4 结 论
根据轧钢厚度控制系统的特点,模型采用自整定控制方式是基于模糊推理系统调优来实现PID控制器参数达到最优值.模糊自整定控制器可以根据系统的输入信号的变化,通过模糊推理决策在线动态地调整PID参数大小.仿真结果表明:模糊自整定PID控制要比传统的PID控制具有达到稳态时间短、消除误差快、控制效果好等优点.轧制过程中,很多因素都会导致系统参数的变化(温度的变化,厚度不均匀).模糊自整定PID控制器采用的是一种新型智能控制方式,与传统PID 控制器相比对于这样的复杂系统具有自整定自调整功能.因此,采用模糊自整定PID 控制器能更好地满足控制系统的实际要求.
参考文献:
[1] Khosravi S,Afshar A,Barazandeh F.Design of a Fuzzy Feed-forward Controller for Monitor HAGC System of Cold Rolling Mill[J].World Academy of Science,Engineering and Technology,2011,5(9):2086-2091.
[2] 行娟娟.轧机液压 AGC 系统数学模型及其控制方法研究[D].西安:西安理工大学,2004:1-5.
[3] 尹腾飞,张玉.模糊PID自整定控制方法在液压AGC系统中的应用[J].制造业自动化,2010,32(10):99-101.
[4] Gong Tao,Qi Lei.Novel ARM-based Gauge Control System with Fuzzy PI Controller[J].International Journal of Multimedia and Ubiquitous Engineering,2012,7(2):527-532.
[5] 王立平,刘建昌,王贞祥,等.热连轧机厚度设定与控制系统分析[J].控制与决策,1994,3(2):115-120.
[6] 王炎,孙一康.基于板形板厚综合控制目标函数的冷连轧机轧制参数智能优化新方法[J].冶金自动化,2002,26(3):11-14.
[7] 张毅,张华,程晓茹.中厚板轧制力数学模型的研究[J].钢铁研究,2005,4(4):18-21.
[8] 杨斌虎,杨卫东,曲蕾.热轧带钢自动厚度控制鲁棒预测模型与控制策略[J].控制理论与应用,2011,28(6):799-804.
