基于ANSYS的减速机齿轮有限元分析

杨金堂，张 珂，全芳成,2，许 海

(1.武汉科技大学机械自动化学院，湖北 武汉，430081；2.武汉钢铁股份有限公司设备管理部，湖北 武汉，430083)

某钢铁厂冶金起重机在作业时，主卷减速机第二级直齿圆柱齿轮的大小齿轮齿根部均出现疲劳裂纹，部分轮齿甚至发生断裂给安全生产带来了严重的隐患。为保证起重机能正常工作，需要从多角度进行分析，找出齿轮轮齿断裂的原因。如果采用传统的计算方法对齿轮轮齿进行应力计算，往往需要简化或对一些参数进行估计，这样会造成计算结果的不准确。为此，本文运用ANSYS有限元软件对该齿轮进行静态特性的模拟，观察分析其在不同载荷情况下轮齿齿根处弯曲应力及应变的变化情况，并结合现场实际情况找出轮齿断裂的原因。

1 断齿形式

该厂减速机的Pro/E三维模型如图1所示，轮齿断口形貌如图2所示，轮齿裂纹形貌如图3所示。观察该故障齿轮可见，断裂的齿轮轮齿裂纹起源于齿根处，一开始裂纹扩展缓慢，几乎与表面平行，而随着裂纹扩展，裂纹与表面间的夹角越来越大，最大夹角近似呈45°。仔细观察断口，发现存在一系列不相交且与裂纹扩展方向垂直的疲劳辉纹，在断口的剪切唇上不仅存在着细小的连结丝，还存在形状呈抛物线的剪切韧窝。由此可以推断，轮齿是在出现疲劳裂纹后，受到冲击载荷的影响产生韧性过载断口，最终导致过载断裂。

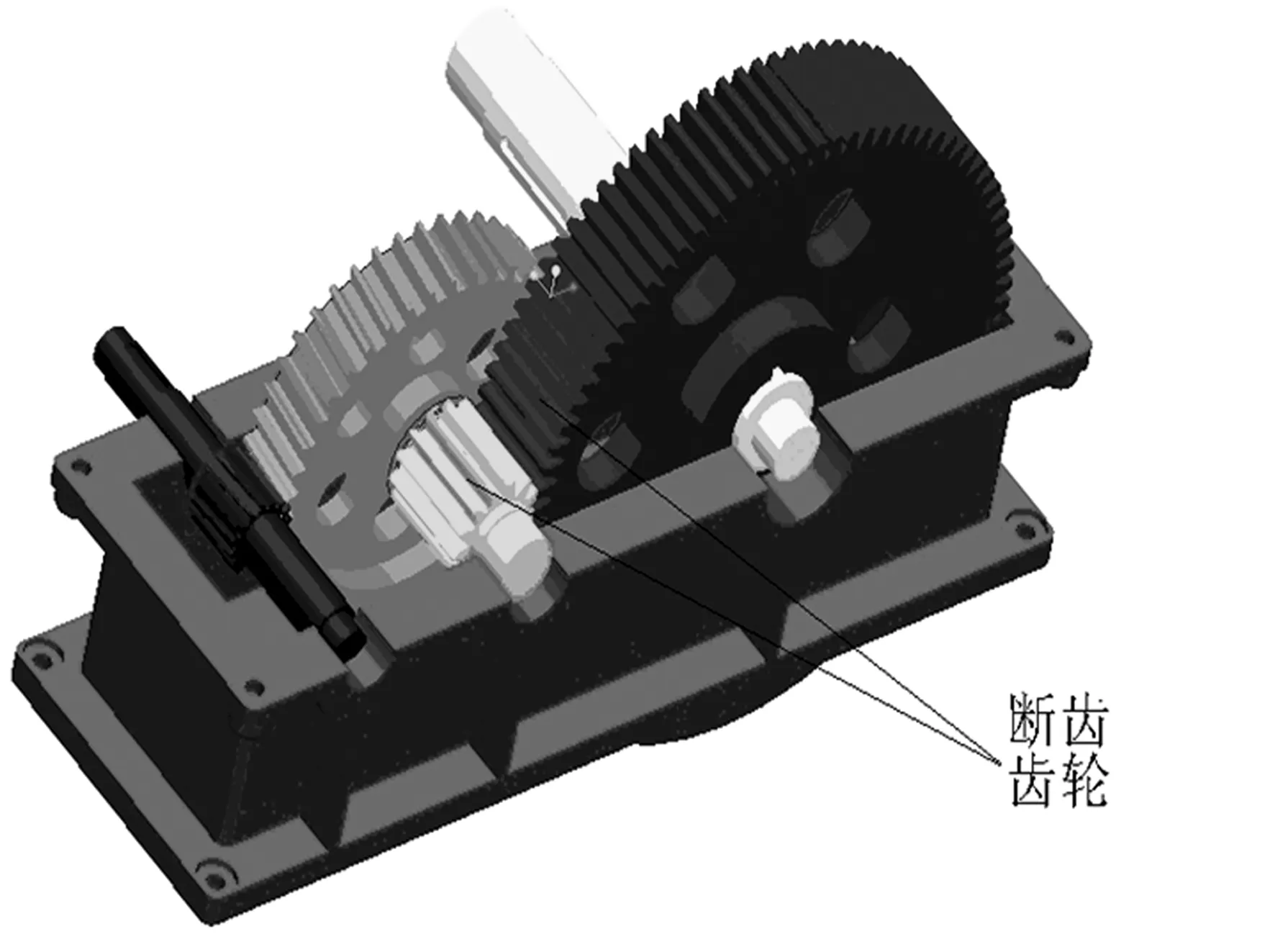
图1 减速机三维模型Fig.1 Three-dimensional model of the reducer

图2 齿轮断齿形貌Fig.2 Morphology of the broken gear tooth

图3 齿轮裂纹形貌Fig.3 Morphology of the gear crack

2 齿轮的基本参数

实际工作过程中，和大齿轮配合的是齿轮轴，为了分析方便，将齿轮轴简化为齿轮。配合的两个齿轮中，小齿轮材料为20CrMnMo，大齿轮材料为42CrMo。齿轮的弹性模量E=206 GPa，泊松比υ= 0.28，ρ=7.85 g/cm3。电机的额定功率为132 kW，转数为588 r/min。齿轮副的基本参数如表1所示。

表1 直齿轮的基本参数Table 1 Basic parameters of spur gear

由于该齿轮副大、小齿轮轮齿均发生断裂，并且在材料方面，小齿轮轮齿的硬度要大于大齿轮轮齿硬度，故本文只取小齿轮为研究对象。

3 静载荷下齿轮的弯曲应力分析

3.1 有限元模型的建立及网格划分

直齿轮的齿廓曲面是渐开线曲面，根据表1中齿轮的参数，运用ANSYS中的APDL语言，建立齿轮的三维模型。定义齿轮的材料属性，根据计算对象的具体情况、计算的精度要求等因素进行全面分析比较，选择合适的单元形式。为了提高计算精度并减少计算量，选择单元类型为8节点六面体单元So1id185，并选择扫掠型网格。划分结果如图4所示。

图4 齿轮有限元模型Fig.4 Finite element model of the gear

3.2 约束与载荷

对齿轮边界的约束主要是限制圆孔的周向和径向位移，以及两侧面的法向位移[1]，即对齿轮内孔在X、Y、Z方向上的平动进行约束。

齿轮啮合时属于线接触，所以加载时在接触线处进行加载。为了方便加载，将沿啮合线作用在齿面上的法向载荷Fn在节点处分解为2个相互垂直的分力，即圆周力Ft与径向力Fr，载荷的大小可根据设计承载的扭矩公式求得：

(1)

Fr=Fttanα

(2)

式中：T为小齿轮传递的转矩，N·mm；d为小齿轮的分度圆直径，mm。

根据表1参数，由式(1)和式(2)计算可得Ft=17 508.35 N，Fr=6372.52 N。

3.3 仿真结果与分析

小齿轮施加静载荷后的等效弯曲应力云图如图5所示。由图5中可知，最大弯曲应力分布在齿根部分，其值为691.807 MPa，小于齿轮的许用弯曲应力775.83 MPa，表明在静载荷作用下，该齿轮符合强度要求。

小齿轮施加静载荷后的位移矢量图如图6所示。由图6中可知，齿轮在外力的作用下轮齿的最大变形量为0.243 mm，变形量不大。

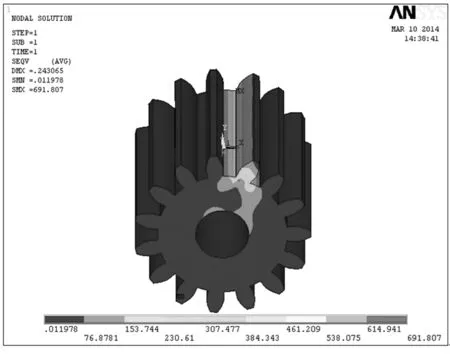
图5 静载荷下齿轮的等效应力图Fig.5 Stress nephogram of the gear under static load

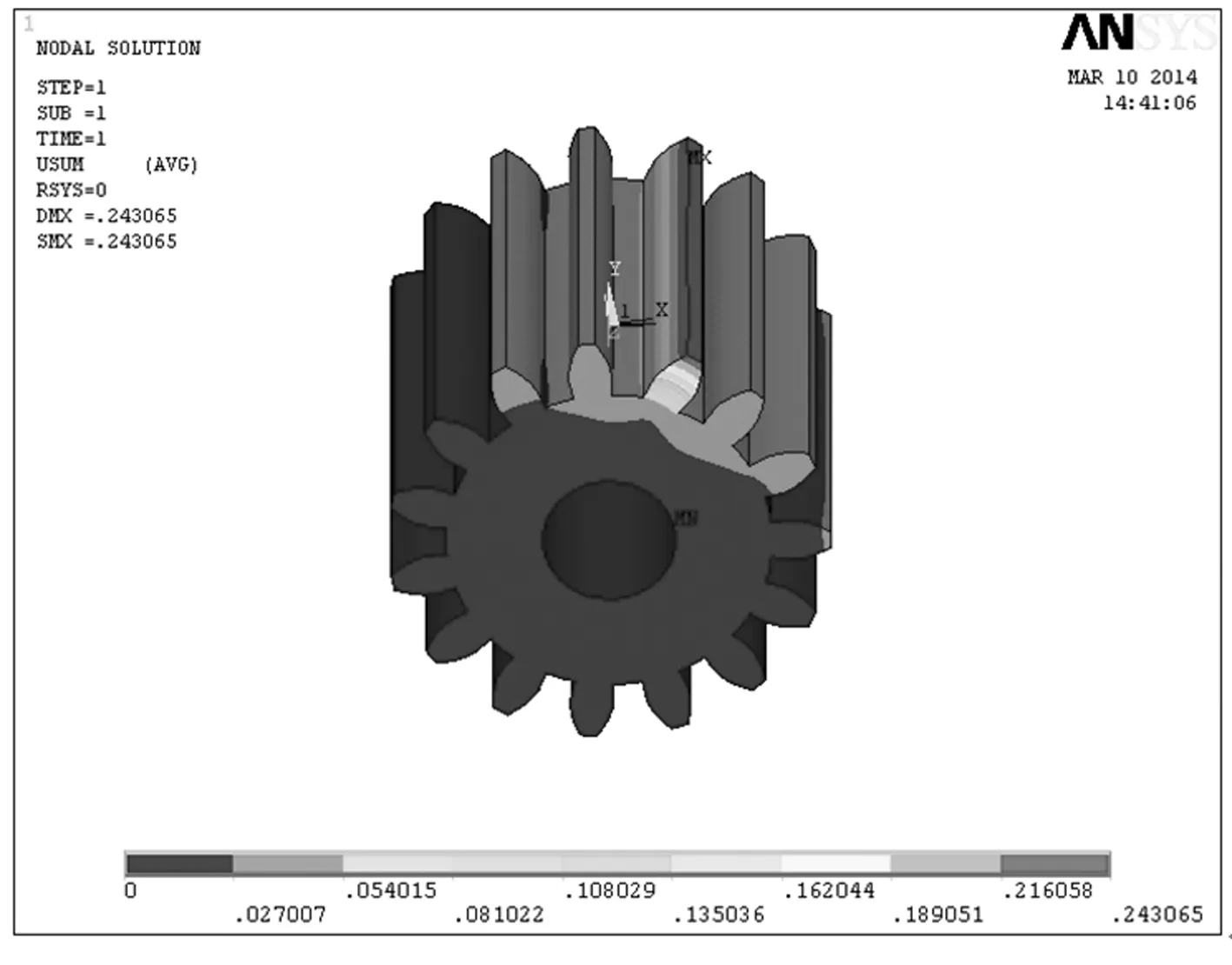
图6 静载荷下齿轮的位移矢量图

Fig.6Displacementvectordiagramofthegearunderstaticload

4 考虑动载荷的齿轮弯曲应力有限元分析

依据上述分析，齿轮轮齿在静载荷的作用下，虽然齿根部所受到的弯曲应力较大，但都在许可的范围内，其应变也在允许的范围之内。但是，实际生产中，冶金起重机工作环境较为复杂，不可避免地会受到振动冲击的作用，特别是起重机主梁钢结构引起的振动冲击、起升质量突然离地起升或下降制动时产生的冲击[2]以及齿轮啮合时产生的冲击，这些因素都有可能造成齿轮断裂。因此，在齿轮弯曲应力的分析中，不可忽视动载荷的影响。

4.1 齿轮的动载荷计算

齿轮啮合时受到冲击的过程较为复杂，为了计算方便，以受到冲击一瞬间的齿轮轮齿为研究对象，并将此时的动载荷假定为一固定值。依据冲击理论，运用下式可近似求得齿轮所受的动载荷[3]：

(3)

式中：fa为弹性构件上的加速力，N；f2为极限变形力，N；W为单位齿宽上名义载荷，N。

由于齿廓存在误差，破坏了轮齿间的共轭关系，导致齿轮速度发生变化，从而在齿轮上产生了加速力。不同的构件，其加速力的影响也不同，但弹性构件上的加速力fa、刚性构件上的加速力f1以及极限变形力f2之间满足以下关系：

(4)

当压力角Ф为20°时，有

(5)

式中：R1、R2分别为大小齿轮的节圆半径，m；m为齿轮在节圆处的有效质量，kg；v为节圆线速度，m/s。

齿轮在啮合过程中，轮齿在载荷作用下会发生弯曲变形，则对于压力角为20°的齿轮，其轮齿的总变形量ξ为：

(6)

式中：E1、E2分别为主、从动轮的弹性模量，N/mm2；b为齿轮的齿宽，mm。

当考虑齿轮制造误差时，齿轮的极限变形力为：

(7)

式中：e为齿轮的制造误差，mm。

齿宽上的名义载荷W=Ft=17 508.35 N，由式(3)计算可得齿轮的动载荷Wd=60 328.15 N。

4.2 ANSYS有限元分析结果

此处有限元分析过程与静载荷下的应力分析相同。施加动载荷Wd后，齿轮的等效弯曲应力云图和位移矢量图分别如图7和图8所示。从图7中可以看出，在动载荷Wd作用下，齿根处的弯曲应力最大为2720.48 MPa，其值远远大于静载荷下齿根的最大弯曲应力值(691.807 MPa)，且超过了齿轮的许用弯曲应力值(775.83 MPa)。由图8中可以算出，此时轮齿的最大变形量为0.969 mm，变形量较大，会使齿轮出现较为明显的裂纹，甚至会发生断裂。

图7 动载荷下齿轮的等效应力云图Fig.7 Stress nephogram of the gear under dynamic load

图8 动载荷下齿轮的位移矢量图

Fig.8Displacementvectordiagramofthegearunderdynamicload

4.3 齿轮弹塑性接触应力的计算

根据上述分析，轮齿在动载荷的作用下，齿根的应力超过了材料的屈服极限，则会产生残余应力和残余应变。

根据弹塑性力学，有Von Mises屈服条件：

f(σij)=(σx-σy)2+(σy-σz)2+(σz-σx)2+

(8)

式中：k为纯剪切状态时的屈服应力。

由弹塑性力学可知，在拉压状态下，若最大剪应力达到临界值k时，会发生塑性变形。对于直齿圆柱齿轮，其轮齿上各点的最大剪应力可用摩尔应力圆的半径表示[4]，即

(9)

通过计算求解可知，随着载荷的增大，在轮齿的接触区中心处，齿面间接触的最大压力为p0=3.1k，此时的τmax将达到k值[5]。

由第三强度理论有：

(10)

式中：σs为齿轮材料的屈服极限，N/mm2。

由式(9)和式(10)可得齿轮材料的弹性极限为：

Plim=1.55σs

(11)

根据文献[6]，σs=931 MPa。由式(11)计算可得Plim=1443.05 MPa，而通过ANSYS软件计算的齿根处最大弯曲应力为2720.48 MPa，远大于该Plim值，由此可以推断，齿轮轮齿断裂是由于过载冲击造成的。这验证了前面经验判断的准确性。

5 预防措施

通过对齿轮的有限元分析可知，在正常的工作条件下，齿轮是满足强度要求的，并且设计人员在设计时一般会考虑到突发情况，即冲击带来的影响，但是由于起重机工作环境复杂，在较高的动载荷作用下，齿轮上受到较大弯曲应力的齿根和其他应力相对集中的部位容易产生裂纹，形成疲劳源，随着重复载荷作用的次数增多，裂纹会不断地扩展，导致齿轮产生疲劳损坏。如果已产生疲劳裂纹的轮齿在冲击载荷的作用下，齿根部位剩余截面上所受到的应力可能超过材料的屈服极限，最终会导致轮齿过载断裂[7-8]。

针对上述所出现齿轮轮齿断裂的问题，可以从以下两个方面进行预防：

(1)从齿轮的设计制造阶段来看，可选用较大的齿轮模数，降低齿根弯曲应力，提高齿轮的弯曲强度。

(2)在使用阶段，冲击载荷峰值大并且时间较短，多为偶发因素，需要减少或者避免工作过程中出现冲击载荷。另外齿轮偏载会引起应力集中，使得齿轮局部应力超过承载能力而发生断裂，因此可以通过提高安装和装配质量来减少齿轮偏载。

[1] 朱彤.齿轮弯曲应力的有限元分析[J].苏州市职业大学学报, 2008,19(4):22-23.

[2] 孙民，王志远，付为刚.桥式起重机起吊过程的动力学分析[J].机械，2010，37(5):12-14.

[3] 朱孝录，鄂中凯.齿轮承载能力分析[M]. 北京：高等教育出版社，1993:46-47.

[4] 廖海平，刘启跃.齿轮塑性变形失效的安定极限分析[J].西南交通大学学报:自然科学版，2010,45(5)：676-680.

[5] Halling J.摩擦学原理[M].上海交通大学摩擦学研究室，译.北京:机械工业出版社，1981:48-51.

[6] 机械设计手册编委会.机械设计手册(齿轮传动)[M].北京:机械工业出版社，2007.

[7] 严范梅，王明辉.齿轮断齿失效分析[J].现代制造工程，2005(7):128-129.

[8] 程军红，范福玲，邱宝年.解决齿轮轮齿断裂问题的有效方法[J].机械传动，2002,26(3)：52-53.