基于主成分分析和高斯混合模型的耐火材料损伤信号分类
2014-03-26周海涛王志刚刘昌明
周海涛,王志刚,刘昌明
(武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081)
耐火材料损伤形式的检测、分类和识别对于保障高温设备的正常安全运行非常重要[1-2]。一些微观结构复杂的复合耐火材料受损时产生的声发射信号极为复杂,要对该损伤信号进行分类十分困难,其中包含分类指标的选择。关于指标的选定已有不少研究。Jeng 等[3]在对炭纤维热塑性复合材料断裂机制的研究过程中,研究了声发射信号参数中延时分布、上升时间、能量及峰值振幅等参数的特征,并将其作为区分不同破坏机制的有效特征,从而将纤维断裂及脱层两种破坏形式区分出来。Yamaguchi 等[3]在对玻璃纤维复合材料的研究过程中,关注了信号能量矩这一参数,发现其分布比峰值幅度分布更为有效,并将其用来区分玻璃纤维材料中纤维断裂和脱胶开裂两种损伤形式。金周庚[4]等研究了B-Al复合材料变形和断裂过程中的声发射特征,发现声发射振幅、振铃计数和费利西蒂比等参数可以用来识别复合材料的损伤形态。上述区分指标均局限于声发射信号参数中各自感兴趣的某些参数,结果显然会造成信息遗漏,分类结果也难免有大的差异。
主成分分析(PCA)法是通过线性变换从多个变量中选出较少个变量的一种多元统计分析方法[5]。高斯混合模型(GMM)是用高斯概率密度函数精确地量化事物,将其分解为若干基于高斯概率密度函数所形成的模型[6]。本文运用主成分分析(PCA)方法,对MgO-C耐火材料损伤实验获取的15个声发射参数进行消除相关性降维处理,得到信息全面的两个新参数,再采用高斯混合模型将信号分为两大类,最终用扫描电镜验证了分类的合理性。
1 主成分分析构造新指标
记样本的观测矩阵[7-8]为
(X1,X2,…,Xp)
(1)
式中:样本矩阵X的每一行对应一个声发射信号的全部参数,每一列对应一个参数的不同信号值。
记样本的协方差矩阵
(2)
为∑的估计。
步骤1:以S构造出样本矩阵X的协方差矩阵
∑=
(3)
式(3)为P×P对阵矩阵,且为正定矩阵,故有P个互不相等且大于零的特征值,每一特征值均对应一个单位特征向量。
步骤2:求出P个特征值及其对应的特征向量
设:λ1,λ2,…,λp为S的P个特征值;T=t1,t2,…,tp为相应的单位特征向量。将特征值按从大到小顺序排列为:
λ1≥λ2≥……≥λp≥0
(4)
步骤3:定义特征值贡献率和累计贡献率分别为
(5)
(6)
A=(t1,t2,…,tm)
(7)
步骤5:用该特征向量矩阵和样本矩阵作线性变换
通过上述步骤,将原来P个指标降维成m个指标,这m个指标均包含最大信息量且相互线性无关。
2 高斯混合模型分类
高斯混合模型概率密度函数定义如下:
(8)
式中:M为模型的混合数;ωk为混合模型的权重系数,且∑ωk=1;N(x|μk,∑k)为第k个单一高斯概率密度函数,为
(9)
估算出合理的参数
θ=[ω1,ω2,ω3,…,ωM,μ1,μ2,μ3,…,
μM,∑1,∑2,∑3,…,∑M]
(10)
使得概率密度函数的最大似然估计值最大,即
(11)
为求解最大似然估计,采用最大期望值(EM)算法对高斯混合模型进行参数估计。EM算法迭代步骤为
步骤1:初始化参数
(1)设均值μ1,μ2,μ3,…,μM为为随机值;
(2)设协方差矩阵∑1,∑2,∑3,…,∑M为单位矩阵;
(3)每个模型的加权系数ω1,ω2,ω3,…,ωM设为每个模型比例的先验概率,即
ωi=1/M
(12)
式中:M为高斯混合模型数目
步骤2:算出各成分在各高斯模型中的先验概率
(13)
步骤3:利用先验概率更新新的参数
(14)
(15)

(16)
步骤4:重复步骤2和步骤3,直至满足收敛条件
|θt+1-θt)|<ε
(17)
式中:θt+1和θt表示前后两次的参数估计值;ε为设定阈值,通常取值为10-5。
3 实例分析
3.1 主成分分析
采集MgO-C耐火材料拉伸、弯曲及断裂过程产生的声发射信号,经声发射软件处理得到15个基本参数为:上升时间(X1)、计数(X2)、能量(X3)、持续时间(X4)、幅值(X5)、平均频率(X6)、RMS(X7)、ASL(X8)、峰值频率(X9)、反算频率(X10)、初始频率(X11)、信号强度(X12)、绝对能量(X13)、中心频率(X14)和峰频(X15),即15个主成分。样本信号总个数为11 168,则样本观测矩阵为11 168×15。为消除各参数间的量纲影响,在进行主成分分析前对样本观测矩阵进行归一化处理,将数据值归一到(0,1)之间,所得协方差矩阵特征值如表1所示。计算每个主成分的累积贡献率,结果如表2所示。由表2中可以看出,前两个主成分的累积贡献率为90.6189%,远大于85%。可见,前两个主成分(指标)足以描述后期所有聚类指标。因此,将其作为新的主成分,设新的主成分为Y1,Y2,这样,参数数目从15维降至2维。
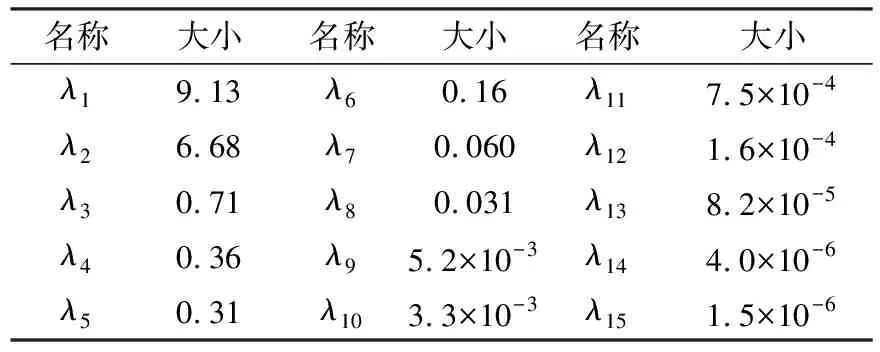
表1 协方差矩阵特征值Table 1 Eigenvalues of covariance matrix
表2每个主成分的累积贡献率
Table2Accumulatedcontributionrateofeachcomponent
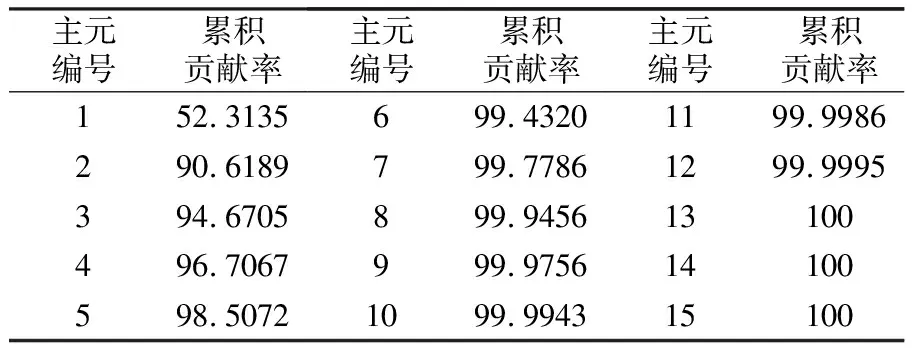
主元编号累积贡献率152.3135290.6189394.6705496.7067598.5072主元编号累积贡献率699.4320799.7786899.9456999.97561099.9943主元编号 累积 贡献率1199.99861299.9995131001410015100
3.2 损伤信号分类
应用高斯混合模型对MgO-C耐火材料损伤信号进行分类。增加模型数目可以提高模型精度,但同时也会增加模型复杂度[9],贝叶斯信息准则(BIC)[10]维持了模型精确度和复杂度之间的平衡,故采用贝叶斯信息准则。
BIC=-2lnL+klnT
(18)
式中:L为估计模型最大似然函数的最大值;T为观测值的数目;k为每个GMM中需要估计的自由参数的数目。
模型数目从M增加到M+1,BIC变化率为
%
(19)
BIC变化率反映了BIC值对模型数目增加的敏感度。当模型数目从M增加到M+1时,如果BIC变化率较大,说明模型数目为M描述原始数据集精度不足,需要增加至M+1个;当BIC变化率较小(<0.03)时,说明M个模型和M+1个模型对原始数据描述的精度差别不大,出于计算成本考虑取M个模型足够。
模型数目BIC变化率如图1所示。由图1中可看出,当模型数目由1增至2时,BIC变化显著,达7%;之后随模型数目增大,BIC变化率逐步减小(<3%)。因此,为节约计算成本,选择模型数目为2用来描述观测数据集。
高斯混合模型运算结果如图2所示。由图2中可看出,MgO-C耐火材料损伤信号被明显分为ω1、ω2两类,其权重值分别为0.63和0.37。
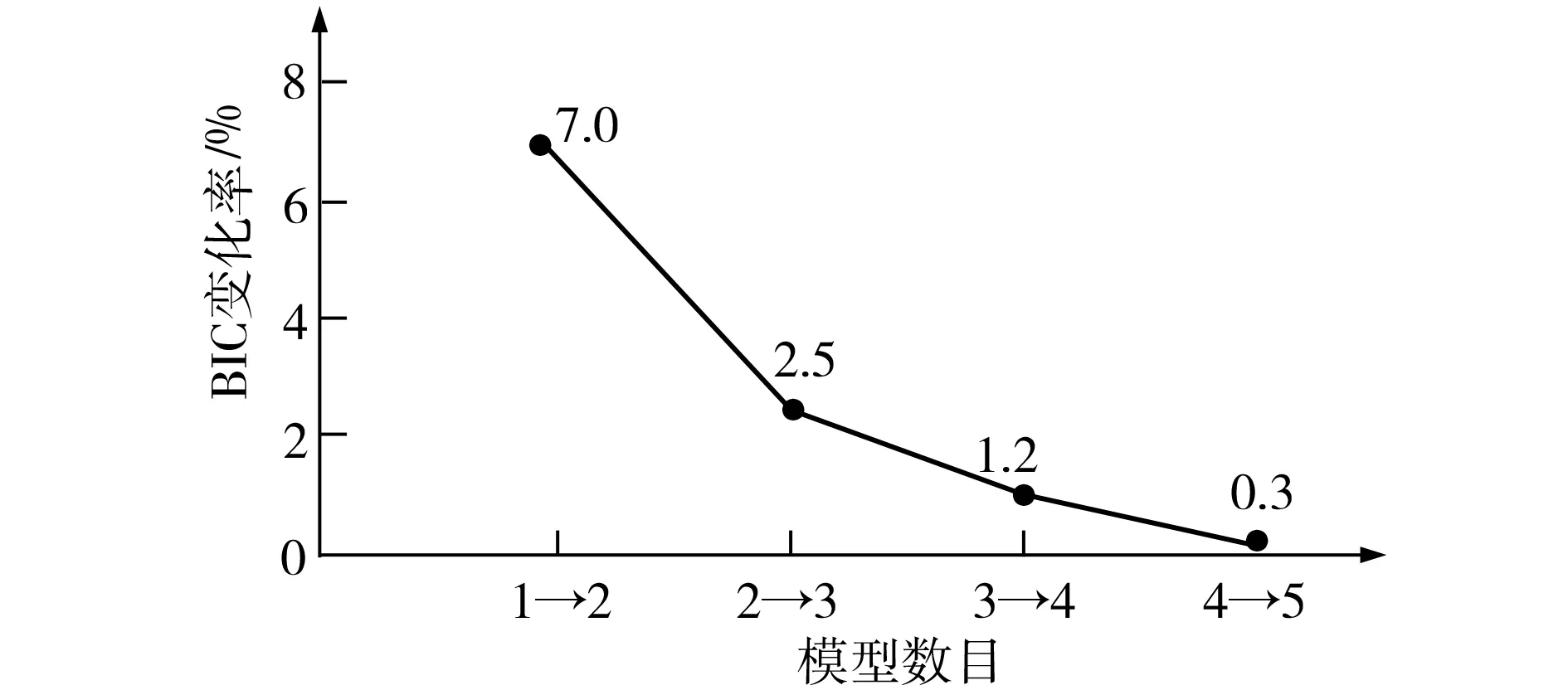
图1 模型数目BIC变化率Fig.1 BIC change rate of each model number
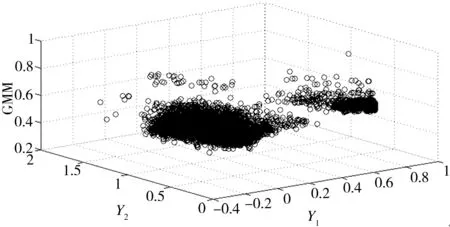
图2 GMM运算结果(ω1=0.63,ω2=0.37)
Fig.2CalculationresultsoftheGMMalgorithm(ω1=0.63,ω2=0.37)
3.3 分类合理性验证
用PHILIPS XL30 TMP扫描电子显微镜(荷兰)配EDAX PHOENIX能谱仪对样本做扫描分析,从扫描结果中可以观察到微观损伤形式主要有基质相损伤裂纹和界面损伤裂纹两种(见图3和图4),且基质相损伤裂纹占大部分比例。两种微观损伤形式的能谱分析结果分别如图5和图6所示。从图5中可看出,基质相损伤裂纹附近主要成分为C,质量分数为97.89%,故该处裂纹为基质相损伤裂纹。从图6中可看出,界面损伤裂纹附近观测点成分以C为主,质量分数为65.78%,此外还存在15.26%的O与18.96%的Mg,表明该处含有基质相与颗粒相,该处裂纹为界面损伤裂纹。上述电镜扫描结果表明,MgO-C耐火材料受载下的主要微观损伤形式为基质相损伤和界面损伤,并以基质相损伤形式为主。至此,验证了主成分分析和高斯混合模型对MgO-C耐火材料损伤信号分类的合理性。

图3 基质相损伤裂纹Fig.3 The matrix damage crack

图4 界面损伤裂纹Fig.4 The interface damage crack

图5 基质相损伤裂纹能谱分析Fig.5 EDS analysis of the matrix damage crack
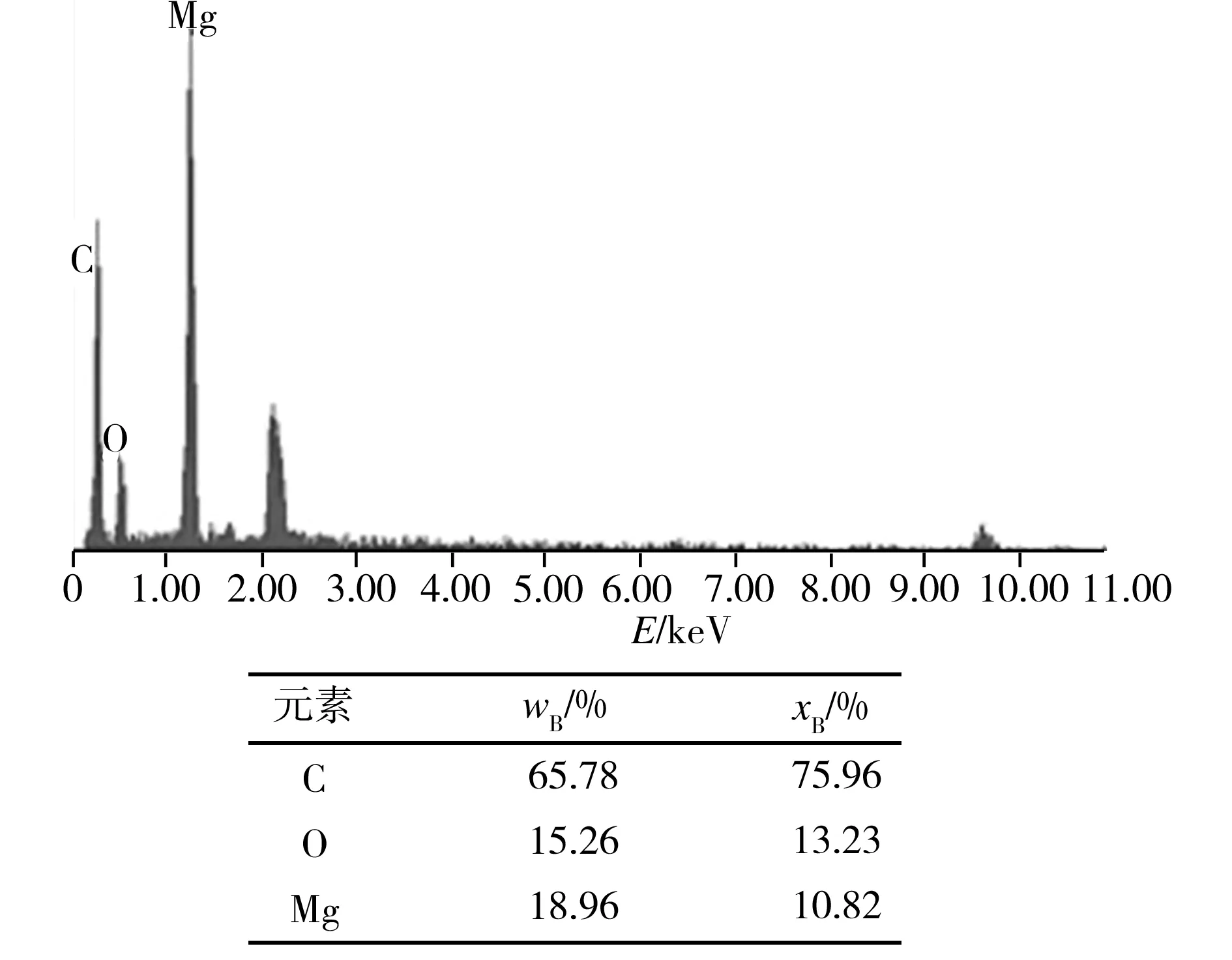
图6 界面损伤裂纹能谱分析Fig.6 EDS analysis of the interface damage crack
4 结语
运用主成分分析(PCA)方法对MgO-C耐火材料损伤实验获取的声发射参数进行消除相关性降维处理,以构造出的新参数作为损伤信号的分类指标,采用高斯混合模型(GMM)聚类方法及贝叶斯信息准则将样本信号分为ω1、ω2两类,其权重分别为63%和37%,扫描电镜验证结果表明,MgO-C耐火材料受载下的损伤形式主要为基质相损伤和界面损伤两种,并以基质相损伤形式为主。
[1] Patapy C,Gault C,Huger M,et al.Acoustic characterization and microstructure of high zirconia elect refused refractories[J].Journal of the European Ceramic Society,2009(29):3355-3362.
[2] 李楠,顾华志,赵惠忠.耐火材料学[M].北京:冶金工业出版社,2010:7-10.
[3] 纪洪广,张天森,张志勇,等.检测中常用声发射参数的分析与评价[J].无损检测,2001,23(7):289-294.
[4] 金周庚,刘哲军,王健,等.B/Al复合材料变形和断裂过程声发射特性[J].稀有金属,1999,23(3):162-165.
[5] 谢晖,樊丁军.统计方法在葡萄理化指标简化中的应用[J].新疆农业科学,201l,27(8):18-21.
[6] 胡庆辉,丁立新,陆玉靖,等.一种快速、鲁棒的有限高斯混合模型聚类算法[J].计算机科学,2013,40(8),191-195.
[7] 党耀国,米传民,钱吴永.应用多元统计分析[M].北京:清华大学出版社,2012:99-108.
[8] 何晓群.现代统计分析方法与应用[M].北京:中国人民大学出版社,1998:281-305.
[9] 吴迪,曹洁,王进花.基于自适应高斯混合模型与静动态听觉特征融合的说话人识别[J].光学精密工程,2013,21(6),33-18.
[10]储岳中.一类基于贝叶斯信息准则的K均值聚类算法[J].安徽工业大学学报:自然科学版,2010,27(4):409-412.
