单层单跨轻型变截面门式刚架结构抗震性能有限元分析
2014-03-26王振山苏明周郭宏超
王振山, 苏明周, 郭宏超
(1.西安理工大学 土木建筑工程学院,陕西 西安 710048;2.西安建筑科技大学 结构工程与抗震教育部重点实验室,陕西 西安 710055)
轻型门式刚架钢结构房屋凭借其结构形式简单、用钢量少、安装方便、工业化生产程度高等优点,在我国低层大空间建筑中应用十分广泛。
由于门式刚架结构自重较轻,以往认为地震作用对其影响较小,故对其抗震性能研究较少。从国内外发生的数次破坏性地震情况来看,门式刚架结构在遭遇强地震作用时,局部会发生屈曲变形,严重的局部屈曲甚至会引起倒塌。
目前,国内相关规范对其抗震设计都未给出具体的设计方法,这对门式刚架结构用于高抗震设防等级区域时的安全性造成了一定隐患。因而对门刚结构进行抗震性能研究是十分必要的,尤其在结构的地震受力性能、变形特征和破坏机理等方面。
Hwang J S[1-2]等对柱脚铰接等截面和变截面门式刚架进行振动台试验研究,对刚架在弹性和弹塑性阶段的变形、内力分布以及结构的破坏模式进行了探讨。Hong Jong Kook[3]进行了变截面门式刚架进行拟静力滞回试验,对其抗震性能进行相关研究并提出了相应的抗震设计方法。申林、胡天兵等[4]应用底部剪力法对单层单跨无吊车门式刚架结构进行抗震承载力计算,得到了通过不同荷载组合应力结果的地震作用控制条件。章军、王元清等[5]对单层单跨门式刚架在风荷载和地震作用下的变形反应进行研究。兰海龙[6]对柱脚铰接变截面门式刚架结构进行抗震性能分析,主要针对自振频率和振型进行研究。肖兵波[7]基于性能理论和美国抗震规范对门式刚架进行了抗震反应分析,提出了适用于我国国情的抗震安全鉴定方法。王传奇、高轩能等[8]利用ANSYS软件,对变截面门式刚架的动力特性进行数值模拟。徐勇等[9]对3/8缩尺模型柱脚铰接变截面单层单跨变截面门式刚架进行滞回试验研究。
本研究在单层单跨门式刚架拟静力试验的基础上,应用有限元软件对全尺寸结构的抗震性能进行研究。
1 门式刚架拟静力试验研究概况
试验试件为一个2榀单层单跨梁柱端板竖放柱脚铰接的1/3缩尺模型,具体加载形式及过程见文献[10]。通过拟静力试验研究发现,门式刚架的破坏形式为结构形成“屈曲铰”的机构破坏,“屈曲铰”相对于塑性铰转动能力差,因而对结构的延性、耗能均产生不利影响。试验结果显示,结构的延性系数μ=1.46,等效粘滞阻尼系数he= 0.121,表明结构进入塑性阶段后,变形较小,耗能能力不高。
2 试验模型有限元验证
ABAQUS是一款功能强大的有限元软件,可以用来模拟庞大复杂的模型,能有效解决工程实际中大型模型的高度非线性问题。
首先,通过ABAQUS中的CAE前处理模块,根据试验试件的几何尺寸建立有限元模型,具体形式见图1。
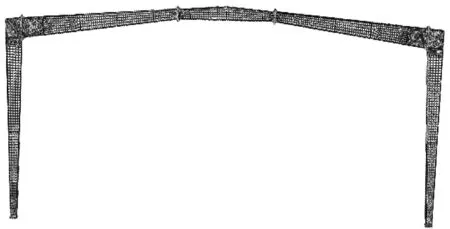
图1 有限元模型
根据材性试验测试结果,钢材的弹性模量E=2.09×105MPa,屈服强度fy=320 N/mm2,抗拉强度fu=420 N/mm2。钢材的屈服准则采用Von-Mises屈服准则,材料的强化本构关系选取各向同性强化模型,不考虑包辛格效应。采用上述本构关系可较好地表示塑性阶段材料的应力-应变情况,形式简单,且能满足计算精度的要求。有限元单元采用减缩积分C3D8单元,减缩积分单元比普通完全积分在每个方向上少用了一个积分点,计算速度更快,该单元对位移求解较精确,网格抗扭曲能力强,在弯矩荷载作用下不易发生剪切自锁[11]。模型荷载与试验情况一致,加载制度见图2。
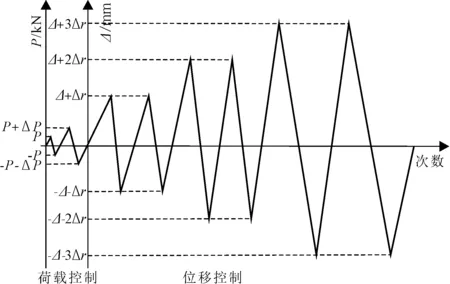
图2 有限元模型加载制度
2.1 破坏形式比较
有限元模型破坏形式与试验破坏情况对比见图3。有限元模型刚架梁A端(近加载)、B端(远加载)下翼缘发生屈曲变形,其中,B端屈曲位置更靠近节点区。试验试件A端(近加载)、B端(远加载)下翼缘发生屈曲变形,其中,B端发生两处屈曲,破坏位置分别靠近节点区和第一道加劲肋外侧,分析其原因为,试验试件受到初变形、焊接应力等缺陷影响,在第一道加劲肋外侧部分形成薄弱区域,在荷载作用下发生局部屈曲。总体来看,有限元模型破坏形式与试验结果吻合程度较好。
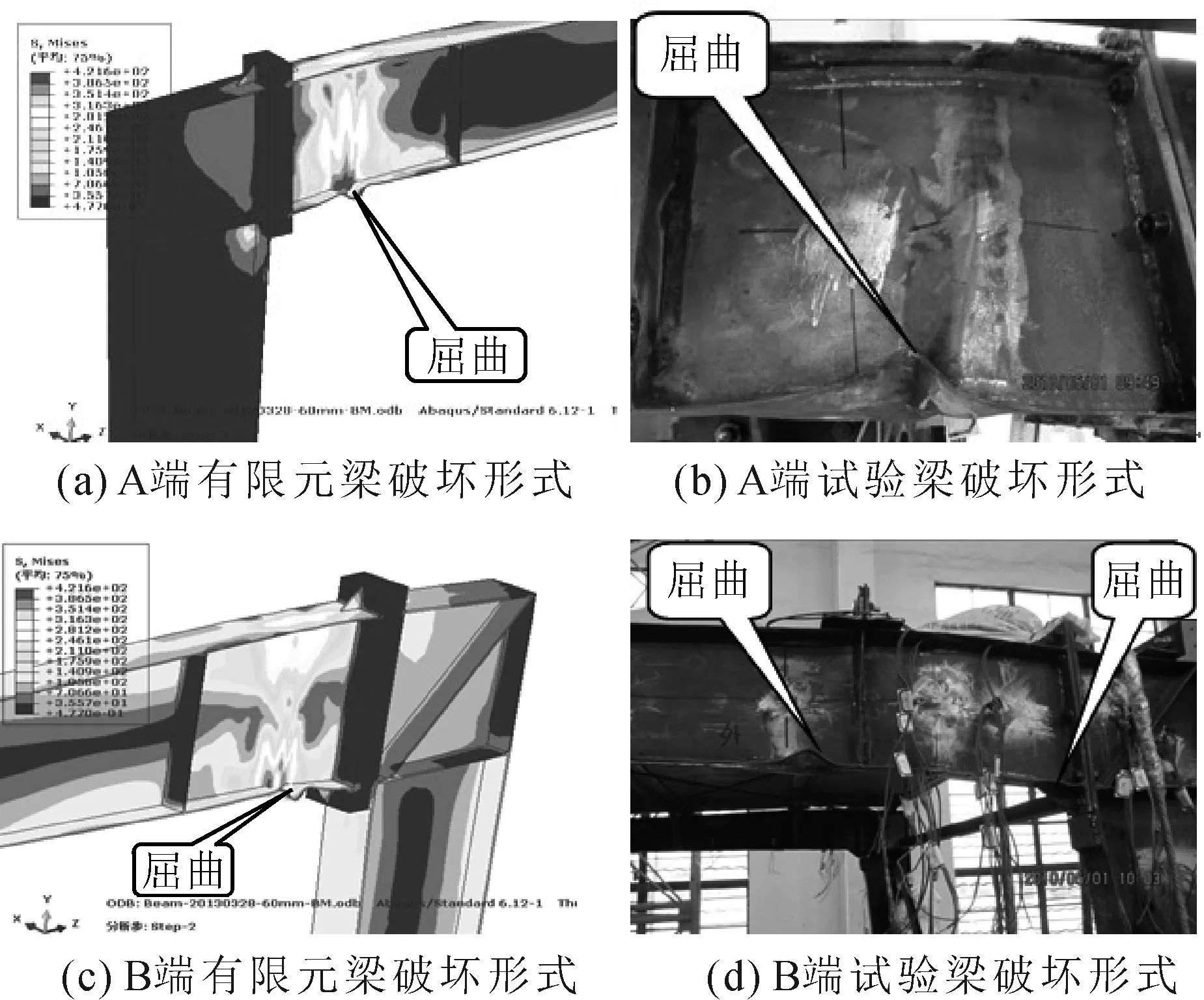
图3 数值模拟结果与试验破坏对比
2.2 滞回曲线与骨架曲线比较
有限元模型与试验荷载-位移滞回曲线对比见图4,有限元模型与试验骨架曲线对比见图5。分析可知,有限元模型滞回曲线和骨架曲线的变化范围、形式和规律与试验结果吻合程度较高。
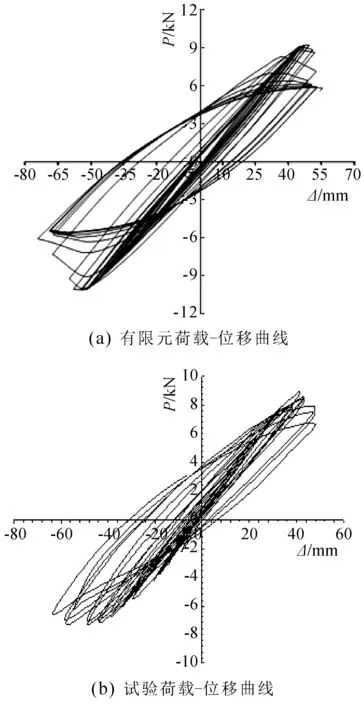
图4 荷载-位移滞回曲线对比
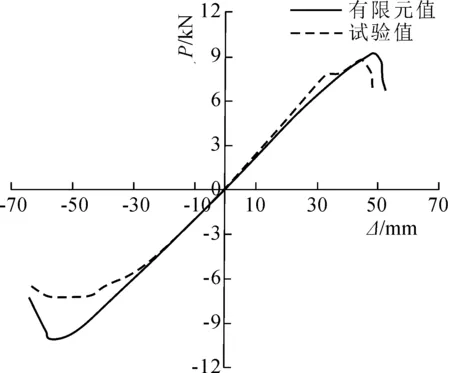
图5 有限元模型与试验骨架曲线对比
综合上述分析,所建有限元模型可较好模拟门式刚架结构的应力和应变情况,可通过数值模拟得到该结构在水平滞回荷载作用下的破坏形式、承载力和位移情况等,开展抗震性能研究。
3 试验模型原型结构有限元分析
试验通过1/3缩尺模型对门式刚架结构的抗震性能进行研究。由于采用缩尺形式,存在“尺寸效应”,难以反映实际工程中门式刚架的抗震承载力和变形等情况。现对全尺寸结构进行数值模拟,对承载力、位移、破坏形式、延性和耗能情况进行分析,为结构设计提供依据。
有限元模型根据标准图集02SG518-1[12]中的门式刚架进行设计,具体截面尺寸见表1。

表1 门式刚架全尺寸结构
全尺寸结构荷载根据建筑抗震设计规范进行取值计算。柱顶重力荷载代表值为:
G1=G柱半+G墙半=14.4 kN
梁重力荷载代表值为:
G2=1.0G梁+1.0G恒载+0.5G雪载=58.2 kN
去除结构自重,有限元建模时每根刚架柱施加6.21 kN恒荷载,刚架梁施加9.18 kN/m的均布荷载。加载制度按有限元验证模型形式3倍加载。
3.1 原型结构破坏模式分析
全尺寸结构的应力、应变如图6所示。分析可知,全尺寸结构的破坏形式为靠近节点区域梁翼缘发生屈曲,A端破坏区域大约距端板0.5h0(h0为刚架梁大头截面高度),B端破坏区域大约距端板1.5h0。
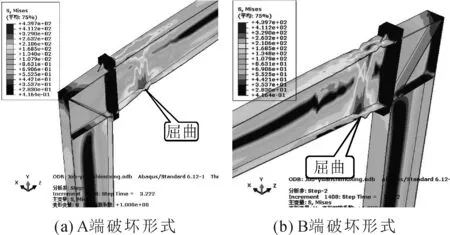
图6 全尺寸结构应力应变
与缩尺模型屈曲形式略有不同的是,全尺寸结构刚架梁上翼缘也发生屈曲变形。另外,刚架梁跨中截面应力较大,这与缩尺模型一致。总体来看,全尺寸结构与缩尺模型破坏形成基本一致,只是结构应力较大区域相对于缩尺模型分布更广,说明应力分布更均匀合理。
3.2 荷载-位移滞回曲线分析
全尺寸结构的荷载-位移滞回曲线如图7所示。弹性阶段中滞回曲线基本呈线形发展,弹塑性阶段中滞回环面积逐渐增大,承载力达到峰值荷载后滞回曲线面积增速加大。当结构承载力达到峰值后,由于全尺寸结构截面尺寸更大,其承载力下降程度较缩尺模型缓慢,滞回曲线也更为饱满。因此,全尺寸结构的耗能能力较缩尺模型更好一些。
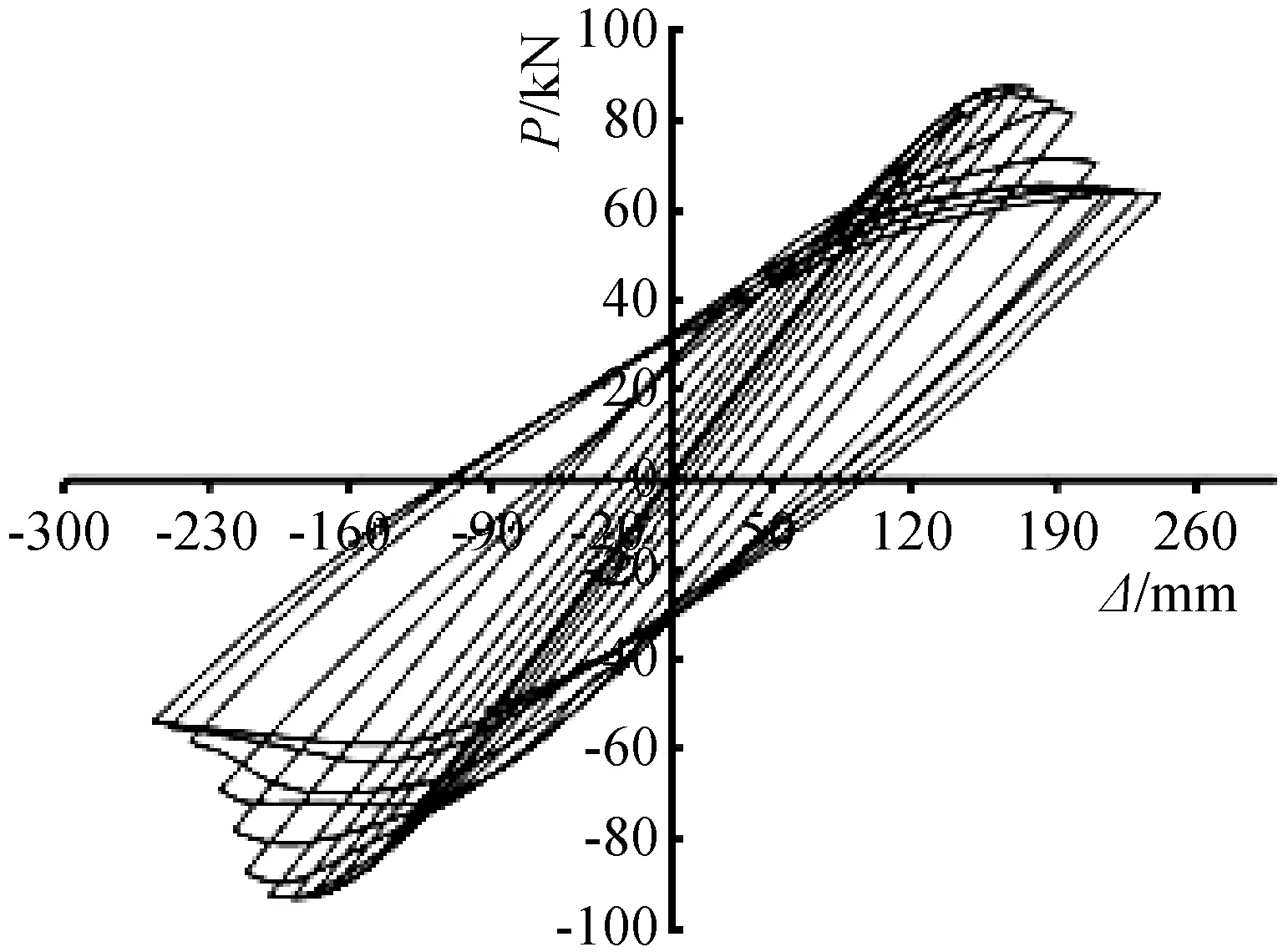
图7 荷载-位移曲线
3.3 骨架曲线分析
全尺寸结构的骨架曲线如图8所示,各阶段荷载、位移特征值见表2。弹性阶段中骨架曲线基本呈线形变化,没有明显的屈服阶段,当结构达到峰值荷载后承载力发生退化,但下降程度较缩尺模型缓慢。另外,正向与负向骨架曲线基本呈对称分布,推拉对结构刚度的影响并不显著。
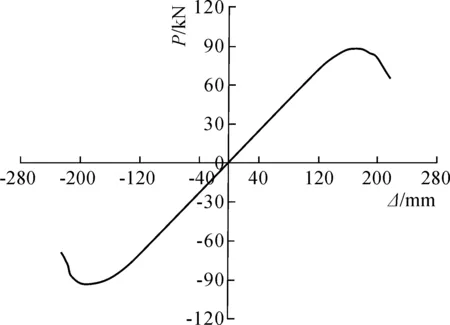
图8 骨架曲线

表2 荷载和位移特征值
3.4 刚度退化曲线分析
全尺寸结构的刚度退化曲线见图9。正、负向刚度退化基本一致,弹性阶段中结构刚度未发生明显退化情况,当翼缘发生局部屈服后结构刚度开始退化,随着荷载增加,尤其是当承载力达到峰值后,刚度退化程度明显加快。由此可见,全尺寸结构的塑形变形能力也较差,与缩尺模型结构基本类似。
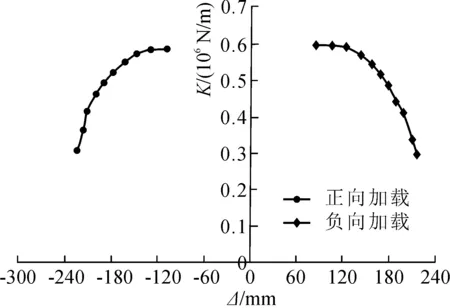
图9 刚度退化曲线
3.5 延性和耗能能力分析
经过有限元计算,全尺寸结构的柱顶最大位移为h/32(h为柱顶高度),结构延性系数μ=1.69。缩尺模型的柱顶水平最大位移为h/43,结构延性系数μ=1.46。可见,全尺寸结构的变形能力和延性性能更好一些。结构的耗能能力可用等效粘滞阻尼系数描述,全尺寸结构的等效粘滞阻尼系数变化见图10。经分析可知,弹性阶段中结构的荷载-位移滞回环面积很小,这里不作统计。当发生局部屈曲后结构进入弹塑性阶段,滞回环面积逐渐增大。当承载力达到峰值荷载后滞回环面积大幅度提高。最终全尺寸结构的等效粘滞阻尼系数 ,缩尺模型等效粘滞阻尼 。可见,全尺寸结构的耗能能力略好一些。
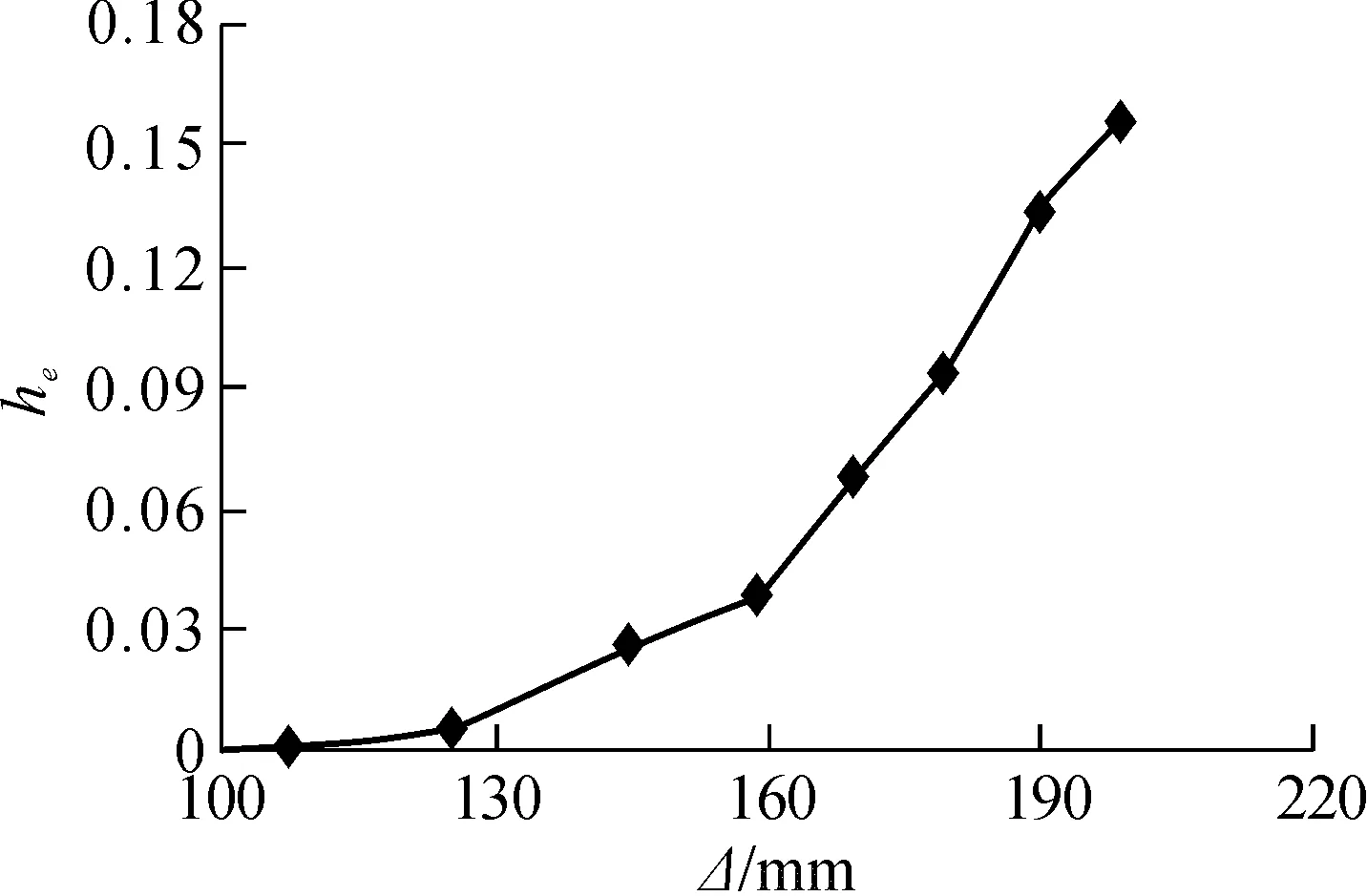
图10 等效粘滞阻尼系数变化
4 全尺寸结构整体抗震性能评估
根据相关设计资料,全尺寸结构的特征周期按III类场地土,地震分组第一组进行取值。根据文献[13] 研究结果,结构自振周期T=0.35 s,阻尼比ζ=0.03。由底部剪力法可算得结构承受的地震水平剪力为:
FEK=αGeq
(1)
水平地震力设计值为:
Pd=FEK·γEH
(2)
式中,γEH为水平地震作用分项系数,取1.3。
经计算,Geq=72.6 kN 。因此,结构在8度多遇地震作用下为:
FEK=η2αGeq=
1.20×0.16×72.6=13.94 kN
结构在9度多遇地震作用下有:
FEK=η2αGeq=
1.20×0.32×72.6=27.88 kN
抗震承载力设计值为:
(3)
式中,γR为材料抗力分项系数,取1.087;γRE为抗震承载力调整系数,取0.75。
结构抗震承载力设计值为:
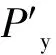
由此可见,虽然全尺寸门式刚架结构延性性能、耗能能力较差,但由于结构自重较轻,承载力较高,在地震作用下,结构仍处于弹性阶段,且承载力有较大的安全储备,实际工程中的门式刚架具有良好的抗震性能。

表3 结构抗震承载力对比值
5 结 论
对全尺寸门式刚架结构进行有限元分析,得到结果为:
1) 全尺寸门式刚架结构在水平循环荷载作用下,破坏模式为靠近节点区域梁翼缘发生屈曲破坏;与1/3缩尺模型破坏形式不同的是,全尺寸结构刚架梁上翼缘亦发生一定程度的屈曲,表明实际的门刚结构破坏时刚架梁的变形更大。
2) 全尺寸门刚的极限位移为h/32(h为柱顶高度),结构延性系数μ=1.69。较缩尺模型有一定的提高,说明其变性能力更强。
3) 分析得到全尺寸结构等效粘滞阻尼系数he=0.163,表明全尺寸门式刚架耗能能力相对更好一些,由于刚架梁上翼缘也发生一定的屈曲情况,形成的“屈曲铰”转动能力增强,结构的耗能能力得到提高。
4) 通过结构抗震性能评估发现:当结构遭遇多遇地震作用时,门式刚架结构仍处于弹性阶段,且安全裕度较大。
总之,全尺寸门式刚架结构的变性能力、延性和耗能较缩尺模型都有一定的提高。
由于结构自重较轻,承载力较高,在地震作用下,结构仍处于弹性阶段,且承载力有较大的安全储备,实际工程中的轻型门式刚架结构具有良好的抗震性能。
参考文献:
[1] Hwang J S, Chang K C, Lee G C, et al. Shaking table tests of pinned-base steel gable frame[J]. Journal of Structural Engineering, 1989, (12): 3031-3043.
[2] Hwang J S, Chang K C, Lee G C. Seismic behavior of gable frame consisting of tapered members[J]. Journal of Structural Engineering, 1991, 117(3): 808-821.
[3] Hong Jong Kook. Development of a seismic design procedure for metal building systems[D]. San Diego:University of California, 2007.
[4] 申林, 胡天兵, 蔡益燕. 门式钢刚架结构抗震分析[J]. 建筑结构, 2002, 32(12): 48-49.
Shen Lin, Hu Tianbing, Cai Yiyan. Seismic performance for steel light-weight portal frame[J]. Building Structure, 2002, 32(12): 48-49.
[5] 章军, 王元清, 陈宏,等. 地震作用下门式刚架轻型房屋钢结构的设计与分析[J]. 四川建筑科学研究, 2004, 30(2): 74-77.
Zhang Jun, Wang Yuanqing Chen Hong, et al. Design and analyse of seismic action on steel structure of light-weight buildings with gable frame[J]. Sichuan Building Science, 2004, 30(2): 74-77.
[6] 兰海龙. 变截面门式刚架的抗震性能[D]. 西安: 西安建筑科技大学, 2004.
Lan Hailong. Earthquake resistant behavior of tapered portal frame[D]. Xi'an: Xi'an University of Architecture and Technology, 2004.
[7] 肖兵波. 既有门式刚架轻型房屋钢结构抗震鉴定方法研究[D]. 上海: 同济大学, 2006.
Xiao Bingbo. Seismic evaluation of existed steel structure of light-weight buildings with gabled frames[D]. Shang Hai: Tongji University, 2006.
[8] 王传奇, 高轩能, 李琨. 变截面门式刚架的动力特性[J]. 福建,泉州:华侨大学学报, 2009, 30(1): 75-79.
Wang Chuanqi, Gao Xuanneng, Li Kun. Dynamic behavior of portal frame structure with tapered members[J]. Fujian,quanzhou:Journal of Huaqiao University, 2009, 30(1): 75-79.
[9] 徐勇, 陈以一, 程欣,等. 轻型门式刚架抗震性能试验研究[J]. 建筑结构学报, 2010, 31(10): 76-82.
Xu Yong, Chen Yiyi, Chen Xin, et al. Experimental research on hysteretic behavior of light-weight steel portal frame[J]. Journal of Building Structures, 2010, 31 (10): 76 -82.
[10] 王振山, 苏明周, 李启才, 等. 单层单跨变截面轻型门式刚架拟静力试验研究[J]. 土木工程学报, 2012, 45(07): 24-30.
Wang Zhenshan, Su Mingzhou, Li Qicai, et al. Pseudo-static experimental research on a single-story single-bay light-weight portal frame with tapered members[J]. China Civil Engineering Journal. 2012, 45(07): 24-30.
[11] 尚军,李自林,张聪,等.型钢混凝土T形短肢剪力墙非线性分析[J].西安理工大学学报,2013,29(3):362-366.
Shang Jun, Li Zilin, Zhang Cong, et al. Nonlinear analysis of T-shaped RC steel reinforced concrete short- pier shell wall[J]. Journal of Xi'an University of Technology, 2013,29(3):362-366.
[12] 中国建筑标准设计研究院. 02SG518-1 门式刚架轻型房屋钢结构(无吊车)图集[M]. 北京: 中国标准出版社, 2002.
[13] 苏明周, 王振山, 王乾,等. 单层单跨变截面轻型门式刚架结构振动台试验研究[J]. 土木工程学报, 2012, 45(10): 98-108.
Su Mingzhou, Wang Zhenshan, Wang Qian, et al. Shaking table test on single-story single-bay light-weight portal frames with tapered members[J]. China Civil Engineering Journal. 2012, 45(10): 98-108.
