梯段爆破过渡区岩体损伤的量化研究

闫建文，徐传召

(1.西安理工大学 土木建筑工程学院，陕西 西安 710048；2.机械工业勘察设计研究院，陕西 西安 710043)

在边坡或水电工程大坝坝肩槽的爆破开挖过程中开挖轮廓线外侧存在一个爆破影响区。该区域位于爆区和爆破远区之间，一般将这一区域定义为过渡区。

过渡区岩体的损伤对边坡及坝肩槽的稳定性具有重要的影响。该区域岩体爆破损伤机理比较复杂,岩体在爆破冲击荷载、爆生气体以及爆破振动的作用下原始裂缝被激活、扩展、贯通, 进而形成新的主裂缝，新裂缝的产生会对岩体产生破坏[1-6]。

本研究运用数学方法，以频率上的能量分布为基础，考虑爆破冲击作用下不同频率能量代表的不同程度的岩体损伤，合理划分频段，计算各频段的能量，量化振动信号不同频段的能量分布，运用神经网络建立过渡区岩体爆破损伤量化模型，实现爆破损伤的量化分析。

1 Hilbert-Huang变换的理论及实现

实现频率上能量分布的关键是找到合理的信号分析方法。

Hilbert-Huang变换[7]是处理非平稳信号的方法。它以局域性的基本量为研究对象[8]从而更接近实际，更适合处理非平稳信号，意义更明确。

Hilbert-Huang变换有两个基本步骤，一个是将信号分解成固有模态函数，另一个是利用相关分解成果进行谱分析。

1.1 经验模式分解

Hilbert-Huang变换独有的优势是以信号的瞬时频率[9]为基础，对信号的局部特性进行分析，主要由EMD和Hilbert变换两部分组成。

EMD是对原始信号进行经验模式分解，以分离出缓变信号，得到固有模态函数(IMF)[10]。

EMD方法的实现过程为：首先对信号序列进行所有极值点的识别，然后根据极值点拟合出X(t)的上下包络线u(t)和v(t)，满足关系式：

v(t)≤X(t)≤u(t)

(1)

对包络线进行平均，即：

(2)

然后，有：

h1(t)=X(t)-m(t)

(3)

h1(t)即IMF，但是h1(t)产生新的极值由于在线条的逼近过程中会产生俯冲和过冲的现象，h1(t)可能会不符合IMF的条件，因此，在此基础上要进一步分解，即：

(4)

h2(t)=h1(t)-m1(t)

(5)

(6)

hk(t)=hk-1(t)-mk-1(t)

(7)

直到hk(t)满足IMF的所有条件，这样就分解到了第一个IMF-C1(t)，即：

C1(t)=hk(t)

(8)

信号的剩余部分用r1(t)表示，为：

r1(t)=X(t)-C1(t)

(9)

对剩余部分重复上述步骤的EMD过程，直到最后的剩余量小于判定值，停止EMD过程，分解结束。

最终，有：

r2=r1-C2, …,rn=rn-1-Cn

(10)

这样，原始信号就可以写为：

X(t)=C1(t)+C2(t)+…+

Cn(t)+Rn(t)

(11)

对于计算的终止条件，黄锷等人[11]提出了确定EMD筛选终止条件的计算公式，即：

(12)

上式中，S值的大小可以根据精度需要确定，一般定为0.3左右。

1.2 Hilbert变换的时频谱与边际谱

HHT是傅里叶变换的一个适合于非平稳信号的发展，它突破了傅里叶变换只能变换为固定频率、常数幅值、全局谱分析的缺陷[12-13]。

对每个IMF进行Hilbert变换，有：

(13)

由此合成的解析信号为：

z(t)=c(t)+iy(t)

(14)

由此得出的时变相位和幅值分别为：

(15)

(16)

瞬时频率为：

(17)

单个分量的Hilbert谱为：

H(w,t)=H(w(t),t)≡a(t)

(18)

然后，对各个分量的Hilbert谱进行叠加得到总的Hilbert谱：

(19)

接着在时间上进行积分，得到信号的Hilbert边际谱：

(20)

h(w)就是边际谱，它的意义是能量而不是振幅，代表能量在不同频率上的叠加。

1.3 爆破振动信号的Hilbert-Huang变换实现

采用辋川河引水李家河水库工程爆破振动检测信号为样本，对其进行HHT分析，信号如图1所示。

由表3可知，试验组小鼠巨噬细胞吞噬率与对照组相比均显著提高(P＜0.05)，其中试验一组的吞噬率与对照组相比提高了14.56%，试验二组吞噬率与对照组相比提高了6.27%，且两个试验组之间差异显著(P＜0.05)。但试验组的吞噬指数与对照组相比差异均不显著(P＞0.05)。

图1 爆破振动信号图

用Matlab实现对实际爆破信号的HHT及其相关分析，该爆破振动信号采用西安市辋川河引水李家河水库工程爆破振动检测信号，采样频率为4 000 Hz，信号如图1所示。

经过HHT后的爆破振动信号的IMF及余量图、爆破振动信号的时频谱图及边际谱图分别如图2～4所示。

图2 爆破振动信号的IMF及余量

图3 爆破振动信号的时频谱图

图4 爆破振动信号的边际谱图

2 过渡区爆破振动特性分析

由于场地的卓越周期为0.17 s左右，因此，在频率4～8 Hz范围内岩体会产生共振作用，该频率范围内的能量为受迫振动的能量。在频率15～25 Hz范围内幅值最大，能量非常集中，代表过渡区爆炸冲击振动的主振频率，25～35 Hz范围内幅值较大，能量较为集中,之后快速衰减。

2.1 过渡区爆破振动的频带划分方法

过渡区岩体爆破损伤量与过渡区爆破振动信号携带的能量的关系是非线性的。过渡区岩体的爆破振动损伤是爆破冲击振动、受迫振动等因素共同作用的结果。不同振动频率携带不同的能量会对岩体造成不同程度的损伤。因此要建立过渡区岩体爆破损伤参量与过渡区爆破振动能量频谱的关系，需要在HHT分解得到爆破振动信号的能量在频率上分布的基础上对信号边际谱进行合理的分解。

对过渡区爆破振动信号能量在频率上的分布进行合理的频段划分并添加合理参量，运用神经网络建立过渡区岩体爆破损伤参量与过渡区爆破振动能量频谱关系的计算模型，达到工程需要的精度，不仅可以加快计算速度，还可以降低对计算硬件的要求，实现应用的广泛性。

在爆破能量频率分布的基础上把频段进行合理的划分。在能量较集中的频率范围，频带划分较细，对于高频成分在爆炸冲击、振动破坏中所起的作用十分微弱，频带划分较宽。

频率大于60 Hz的部分为该孔位叠加所致的能量叠加，在神经网络模式识别下该部分不会起到相应的作用，将该部分舍去。

因此，在前文分析的基础上结合前人的研究成果，将频率的积分区间划分为：4～15 Hz、15～20 Hz、20～25 Hz、25～35 Hz、35～60 Hz五个频段。同时质点最大振动速度在过渡区岩体爆破中代表的是爆炸冲击力的最大值，是工程爆破安全控制中一个极其重要的参数，爆炸冲击力的最大值代表着超越破坏在模型中将爆破振动质点最大振动速度作为一个因素来考虑。

2.2 过渡区岩体损伤的表示方法

岩体在爆破冲击荷载、爆生气体以及爆破振动的作用下原始裂缝被激活、扩展、贯通进而形成新的主裂缝，以及新的裂缝产生，都会使声波产生新的折射、散射、绕射，从而使声波的传递路径与爆破前岩体的传播路径不同，使声速降低。因此，根据爆破前后声速值的变化，可以很准确地判别岩体在爆破冲击荷载、爆生气体以及爆破振动等因素的综合作用下的损伤情况，这就是利用声波检测技术，求得声速变化率以表示岩体爆破损伤参量的理论依据。

3 基于BP神经网络的过渡区岩体损伤量化模型

由于过渡区岩体爆破损伤是由冲击力、冲击振动、受迫振动共同作用的结果，其爆破损伤量与过渡区爆破振动能量频谱的关系是非线性的，这种非线性关系使我们很难通过建立完善的物理理论模型对其进行研究。而神经网络由于具有独特的知识表示结构和信息处理原则而为解决这种非线性关系提供了较好的方法。本研究结合李家河水库工程的实例进行分析。

3.1 李家河水库概况

李家河水库工程位于西安市蓝田县，其任务主要是西安市城东区城镇供水，属Ⅲ等中型工程，永久性主要建筑物拦河大坝按3级设计。坝址区岩性主要为花岗岩，岩性单一、致密坚硬，且具有强度高、模量大、吸水率低等特点。

3.2 BP神经网络建模

神经网络在非线性问题和模式识别问题方面具有独特的优势。其应用已经在很多领域得到了验证。在前文将过渡区爆破振动分解为6个特征因素的基础上，运用神经网络理论，建立数学模型，对过渡区岩体爆破损伤进行量化分析。

按照一般的BP神经网络设计的原则S型正切函数作为中间层神经元的传递函数，因为数据已经全部被归一化，因此把S型对数函数设置为输出层神经元的传递函数。训练函数使用traingdx函数，以梯度下降法进行学习。

网络在训练269次之后达到了要求，如图5、图6所示。

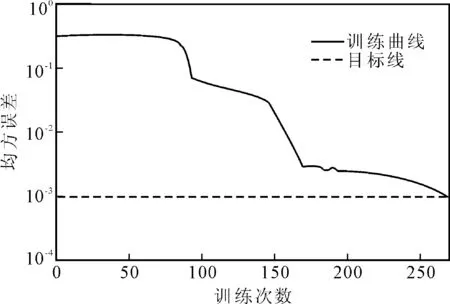
图5 误差曲线

图6 目标曲线

选取三组数据作为测试数据，将识别后的结果进行反归一化，表1是与原数据进行对比的结果。

表1 网络训练结果对比

通过建立BP神经网络模型实现了过渡区岩体爆破损伤的量化识别，岩体爆破损伤识别精度基本满足工程实际需要。

4 结 论

1) 针对梯段爆破过渡区岩体的爆破破坏特性，以振动为研究对象，运用数学方法，建立梯段爆破过渡区岩体损伤的量化模型，实现梯段爆破过渡区岩体损伤的量化分析，将定性的爆破损伤量化对岩体爆破损伤量、损伤范围的界定有一定的帮助，有助于推动进一步的岩体爆破破坏研究。

2) 将模型进行合理简化并与实际工程相结合，达到工程应用的精度，可以实现在爆后较短的时间识别爆破损伤，从而提高爆破损伤评价的效率、降低爆破损伤评价的成本。

3) 对爆破损伤进行量化，对爆破参数的设计、爆破网路的优化有一定的帮助。

4) 本研究为过渡区岩体支护提供理论参考。

参考文献：

[1] Meglis I L，Chow T M，Martin C D. Assessing in situ micro crack damage using ultrasonic velocity tomography [J]. International Journal of Rock Mechanics & Mining Sciences，2005，42(l):25-34．

[2] Otto Schulze，Till Popp，Hermit Kern. Development of damage and permeability in deforming rock salt[J]. Engineering Geology，2001，61(2):163-180．

[3] Sayers C M，Kasyanov M. Micro crack induced elastic wave anisotropy of brittle rocks [J].Journal of Geophysical Research，1995，100(B3):4149-4156．

[4] 中国生，熊正明．基于小波包能量谱的建(构)筑物爆破地震安全评估[J]．岩土力学，2010，31(5)：1522-1528．

Zhong Guosheng，Xiong Zhengming．Safety assessment of structure by blasting seism based on wavelet packet energy spectra[J]．Rock and Soil Mechanics，2010，31(5)：1522-1528．

[5] 晏俊伟，龙源，方向，等．基于小波变换的爆破振动信号能量分布特征分析[J]．爆炸与冲击，2007，27(5)：405-409.

Yan Junwei，Long Yuan，Fang Xiang，et a1．Analysis on features of energy distribution for blasting seismic wave based on wavelet transform[J]．Explosion and Shock Waves，2007，27(5)：405-409．

[6] 闫建文，徐传召，郭仪，等．声波测试技术在李家河水库坝基开挖爆破中的应用[J]．电网与清洁能源，2011，27(6)：85-88.

Yan Jianwen，Xu Chuanzhao，Guo Yi，et a1．Applications of acoustic measurement on lijiahe dam foundation excavation blasting [J]．Power System and Clean Energy，2011，27(6)：85-88．

[7] Norden E H，Zheng Shen，Steven R L. et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454: 903-995.

[8] 路亮，龙源，谢全民，等．爆破振动信号的提升小波包分解及能量分布特征[J]．爆炸与冲击，2013，33(2)：140-147.

Lu Liang ,Long Yuan, Xie Quanming,et al.Decomposition and energy distribution of blasting vibration sign based on second generation wavelet packet(SGWP)[J]．Explosion and Shock Waves,2013,33(2)：140-147.

[9] Comon P. Independent component analysis, a new concept [J]. Signal Processing, 1994,36:287-314.

[10] Belouchrani A, Mariam K A, Cardoso J F, et al. A blind source separation technique using second order statistics[J]. Signal Processing, IEEE Transactions on, 1997,45(2):434-444．

[11] Cardoso J F. Blind Beam forming for Non-Gaussian Signals[J]. IEEE Proceedings-F,1993, 140(6):224-230．

[12] 张义平,李夕兵, Hilbert-Huang变换在爆破震动信号分析中的应用[J]. 中南大学学报,2005,36(5):882-887.

Zhong Yiping, Li Xibing. Application of Hilbert Huang transform in blasting vibration signal analysis[J].Journal of Central South University,2005,36(5):882-887.

[13] 杨凯峰, 牟莉, 许亮. 基于离散小波变换和RBF神经网络的说话人识别[J]. 西安理工大学学报, 2011,27(3): 368-372.

Yang Kaifeng, Mou Li, Xu Liang. Speaker recognition based on discrete wavelet transform and RBF neural networks[J]. Journal of Xi'an University of Technology, 2011,27(3): 368-372.