浐灞流域水质污染分析及评价研究

王颖，孙扬，张丹

(西安理工大学 水利水电学院，陕西 西安 710048)

浐灞流域不仅是陕西省纺织工业、国防制造工业、汽车工业的重要生产地，也是西安市周围农业用水与生活用水的主要来源。

自2002年起，众多高校与科研机构通过对浐灞流域进行相关调研得到大量水质与水文数据，然而如何从繁杂的数据中提取出重要，精简的数据就成为一项亟待解决的问题。

目前常见的数据提取方法有简单指数法、主成分分析法、分级加权平均法及模糊数学法等。对水环境而言，主成分分析法能从诸多影响因素的最终效果入手，排除众多指标之间的相互干扰，通过简化指标来反映水环境压力与水污染防治效果，对各指标之间的关系进行深入的探讨和分析并比较区域间的差异，为水环境的治理提供科学依据[1]。

1 区域水环境概况与研究方法介绍

1.1 区域水环境概况

浐灞流域位于109°00′～109°47′E，33°50′～34°27′N之间。南始秦岭，北至渭河。南北全长75 km，东西宽50 km，流域总面积约为2 581 km2[2]。流域上游区域人口稀少，物种较为丰富，为水源涵养区；中游区域是西安重要的农业生产产业区；下游区域是陕西省重要的工业生产基地[3]。随着浐灞流域周边工业的发展与人口的增长，产生的工业废水与生活污水水量日渐增多并且每个区域的污染特征也不尽相同。

1.2 研究方法介绍

水质研究旨在对多个水质指标进行分析，得出被调查区域的水环境污染状况。虽然每个指标都可以从特定的方面反映出一个监测面的水质情况。但每个指标之间并不是孤立存在的，指标之间均具有一定的相关性，这就加大了对水环境进行综合评价的难度。

目前针对这一问题，很多科研人员为了简化数据，选择从各项水质指标的结果入手，以减少各水质指标之间的干扰。

主成分分析法主要运用的是降维的思想，将大量的具有一定相关性的变量进行线性组合，重新整合为一组新的相互无关的综合数据(一般将这些综合数据称为主成分)来代替原始变量，用以克服原始数据之间的相关性与重叠性[4]，其数学原理如下。

设有n个断面监测点，每个断面监测点有m个水质指标，构成n×m阶原始变量矩阵X：

矩阵X经过标准化处理后得出矩阵Z，通过下式得出数据的相关系数矩阵R后进行数据相关性分析。

(1)

(2)

当得出相关系数矩阵后，为了确保综合评价的准确性，应进行KMO与Bartlett检测。

KMO统计量比较的是样本相关系数和样本偏相关系数，它用于检验样本是否适用于主成分分析法，其定义如下。

(3)

按照Kaiser给出常用的KMO度量的标准,见表1。

表1 KMO度量表

Bartlett球型检验统计量的主要目的是检验相关系数矩阵R与原始矩阵X两者之间是否存在相关性，若两个矩阵之间相互独立，则无法使用主成分分析法来进行数据降维，其定义如下：

(4)

(5)

其中，ln|R|为相关系数矩阵R行列式的自然对数；p为主成分分析中原始变量的个数；q为观测值数，λi为相关系数矩阵R的特征值。当相关系数矩阵R趋近于一个单位矩阵时，|R|趋近于1(记H0)，则ln|R|趋近于0。反之当相关系数矩阵既有大于1，又有趋近于0的特征值时，|R|趋近于0(记H1)，则ln|R|趋近于负无穷。Bartlett检验的判别条件为：

当计算结果为H0时,相关系数矩阵为单位矩阵(即变量互不相关)；

当计算结果为H1时,相关系数矩阵为非单位矩阵(即变量之间存在相关关系)。

SPSS将提供Bartlett球型的卡方统计量、自由度与显著值。若显著值小于0.05，则认为主成分分析法适用于该矩阵，同时卡方统计量越大，变量之间的相关性越强。

由于主成分分析的目的不仅仅在于要找到主成分，更重要的是了解每一个主成分所代表的意义，方便对水质污染特性进行分析。根据相关系数矩阵的不唯一性，可以对相关系数矩阵进行线性组合，即进行主成分旋转，使得每一个水质指标只在一个主成分上具有较大的载荷，而在其他的主成分上的载荷较小，以便于主成分的分析。

对相关系数矩阵进行旋转后，需求解出相关系数矩阵与旋转后矩阵的m个特征值与对应的特征向量，并得出m个主成分数据，由于各个主成分的方差是递减的，包含的信息量也是递减的，所以在一般计算时根据主成分累计贡献率的大小选取前k个主成分。贡献率是主成分的方差占全部方差的比重，实际也就是某个特征值占全部特征值的比重，其计算公式如下所示：

(6)

贡献率越大，说明该主成分所保留的原始变量信息就越多。

主成分个数k的选取，主要根据主成分的累计贡献率来决定，一般要求累计贡献率达到85%以上，才可以保证主成分能包括原始数据的绝大多数信息[5]。选取好k个主成分后，对其进行加权求和，计算每个主成分的得分，其中权数是每个主成分的方差贡献率，并在排名后进行评估。

通过主成分分析法进行数据整合不仅可以得出具有代表性的主成分，达到简化数据与减少干扰的目的，还可以通过主成分为水质治理工作提供具有针对性的科学依据。

因此，本文将对浐灞流域水质指标运用主成分分析法进行综合评价，并借助SPSS19.0版进行数据处理工作。

2 浐灞流域水质分析及评价

2.1 水质分析

此次研究的数据为浐灞流域2013年18个断面的7个水质指标的年均值。其中浐河地表水的监测面3个(浐河入区口、华清桥、浐河口)，灞河地表水的监测面4个(灞河入区口、灞河口、浐灞河交汇口、三郎村)，雁鸣湖的监测面3个(2号湖出口、4号湖出口、5号湖出口)，世园会的监测面4个(中湖、北湖入口、西湖、出口)，湿地公园的监测面4个(功能湿地出水、天池、蒹葭湖、湿地公园出水)共18个监测面。

图1 各监测面取水点示意图

在每个监测面选取7项常用的水质评价指标(电导率、溶解氧、高锰酸盐指数、化学需氧量、氨氮、总氮、总磷)作为分析依据。首先分别对18个断面的7个指标进行基本统计分析(见表2)。

由表2可知，电导率方差最大，为24 349.433，说明极大值和极小值相差最大，可以反映出电导率的监测数据在不同监测面差别最大；而总磷的方差最小，为0.026，说明总磷在不同监测面的监测数据差距最小[6]。

经过基础的数据统计分析后，运用SPSS软件对原始数据进行标准化后求出各水质指标相关系数矩阵(见表3)。

在得出相关系数矩阵后需要进行KMO和Bartlett检验，若能通过检验才能确保相关系数矩阵分析的准确性，若不能通过检验则需对数据进行筛选。

表2 统计量描述

表3 各水质指标相关系数矩阵

本次分析所得的KMO度量(见表4)为0.783，接近0.8合适的标准，代表本次数据可以使用主成分分析法进行分析。并且Bartlett的球形检验的近似概率小于0.01，从而可以否定相关矩阵为单位矩阵的假设，说明各污染物之间存在显著的相关性，表明主成分分析法适用于浐灞流域水质研究。

表4 KMO和 Bartlett 的检验

相关系数矩阵中若两个指标之间的相关系数的绝对值越大，则这两个指标之间的联系越紧密[7]。从表3可以看出，不同指标之间，化学需氧量与高锰酸盐指数之间的相关系数最高为0.967，说明这两个指标之间的相关性最强，同时总氮与氨氮、总氮与总磷之间也具有很强的相关性，其相关系数分别为0.934和0.901。反之，溶解氧与化学需氧量之间的相关系数的绝对值仅为0.200，说明两者的相关性是最弱的。

经过对相关系数矩阵的简单分析后，根据相关系数矩阵求出其相应的7个特征值，并计算出主成分的累计贡献率，根据累计贡献率确定主成分的个数(见表5)。根据累计贡献率大于85%的提取原则，在7个主成分中前3个主成分的累计总方差为94.420%满足提取原则，所以选取的主成分个数为3个。

表5 水质指标方差分解及主成分提取分析表

运用SPSS软件计算出累计贡献率后，自动得出碎石图(见图2)，可以直观地看出，第三个主成分后的特征值变化趋势变缓，证明选取3个主成分分析是比较适合的。主成分方差如表6所示。从表6可以得知，溶解氧的提取值为99.7%，可以解释为样本提取的3个主成分代表了原始数据中99.7%的溶解氧数据，其他变量的解释也与此相同。

表7是旋转后成分矩阵，主要反映了各水质指标的载荷绝对值与提取的3个主成分之间的相对系数，对一个污染物来说，载荷绝对值较大，则对应的主成分与它的关系也较为密切，也更能代表这个水质指标。

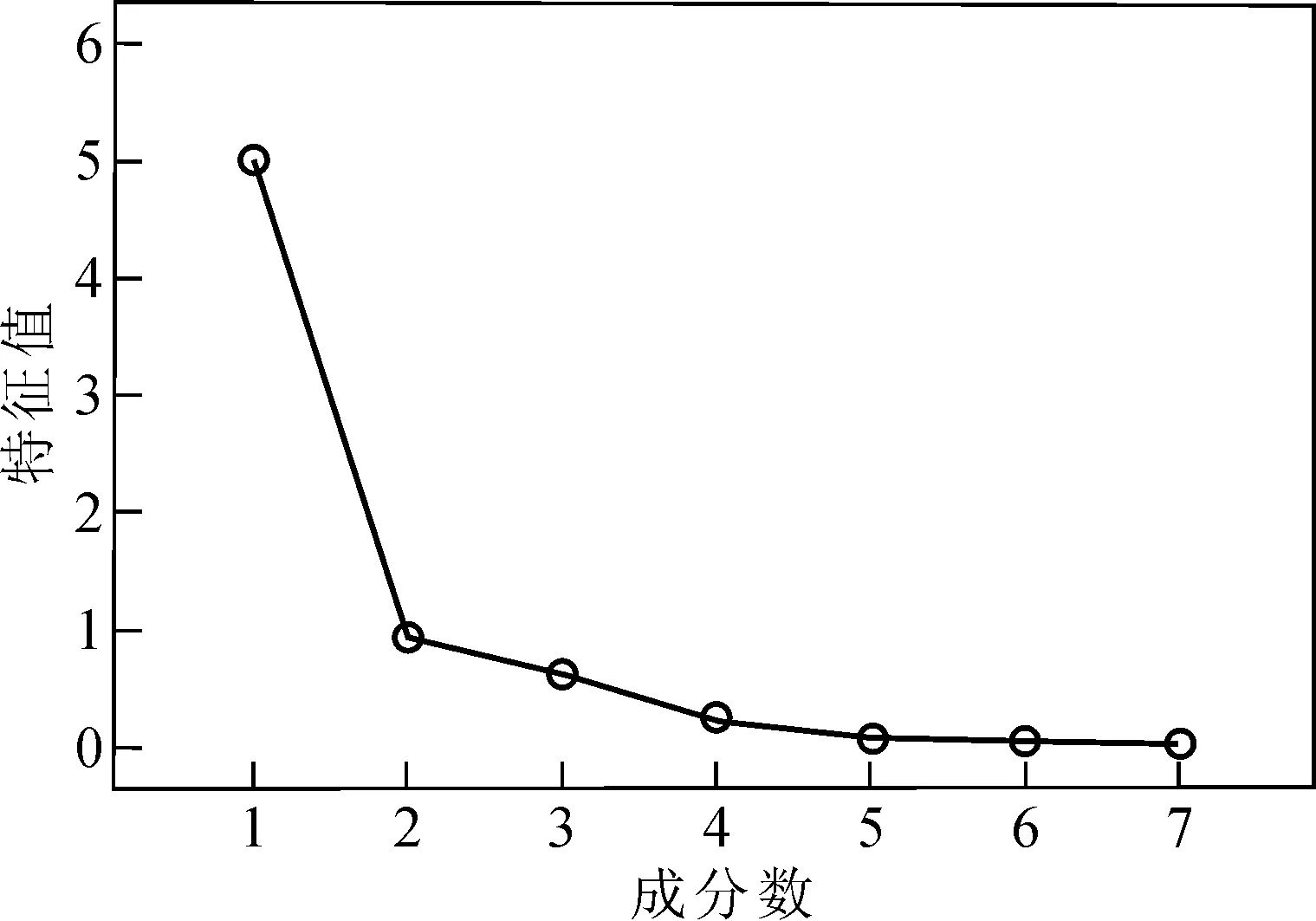
图2 碎石图

表6 主成分方差

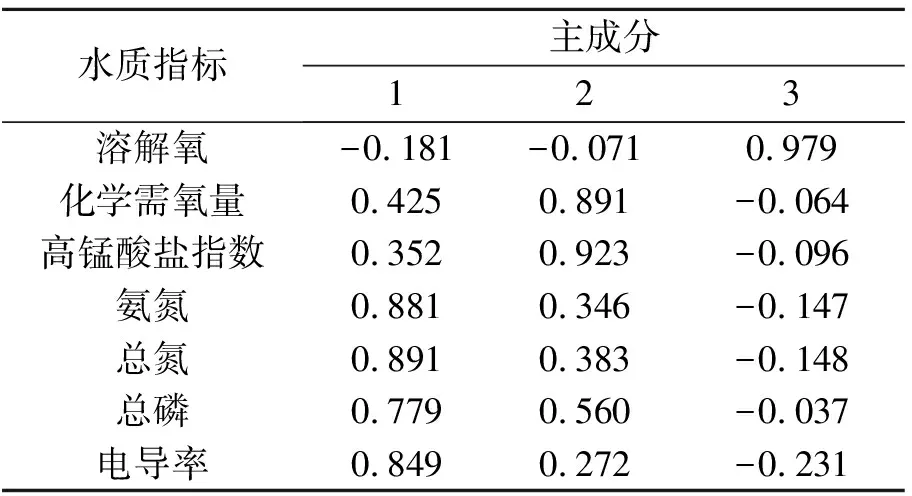
表7 旋转后成分矩阵

提取方法:主成份；旋转法：具有Kaiser标准化的正交旋转法，旋转在经过6次迭代后收敛。

基于这个观点，主成分1能较好地代表总氮、总磷、氨氮、电导率四项水质指标的影响；主成分2能较好地代表高锰酸盐指数与化学需氧量两项指标；主成分3能较好地代表水中溶解氧的含量。这样就可以使用所提取出的3个主成分描述18个监测面的受污染状况，并用3个主成分的得分系数与18个点的7个指标进行计算，得出每个主成分的分数，计算公式为(其中各指标得分系数均在表8中详细列出)：

(7)

式中Fi为第i个主成分的得分，Pj为各水质指标，Cij为第i个主成分下第j个水质指标的得分系数。

表8 成分得分系数矩阵

提取方法:主成份; 旋转法:具有 Kaiser 标准化的正交旋转法。

再利用每个主成分的方差贡献率与成分得分的乘积可以得出最后的综合得分，计算公式为：

(8)

式中zF为综合得分，Hi为主成分i旋转后的方差贡献率。

表9中综合得分排名显示了监测面水质受到污染的轻重程度，浐河口和三郎村综合得分较高，水质较差。

表9 各主成分得分与排名及综合得分与排名

如果按提取的3个主要成分得分进行排名,并取各自前三,则结果如下。

主成分1得分前三的依次是是浐河口、三郎村、浐灞河交汇口这3个监测面，表示受到总氮、总磷及氨氮的影响最为明显，同时三者对电导率的数值变化敏感，说明区域水质中杂质含量与含盐量较高。目前我国地表水环境质量标准中未将电导率纳入其中，但通过电导率可以有效地反映出水样中的含盐量与水中杂质含量，因此在进行水质试验与数据分析时，电导率是不可缺少的指标之一。

主成分2得分前三的依次是北湖入口、2号湖、中湖这3个监测面，表示这3个监测面对高锰酸盐指数与化学需氧量两项水质指标的变动较为敏感。

主成分3得分前三的依次是北湖入口、中湖与灞河口这3个监测面，表明这3个监测面受到溶解氧的数值变动最为敏感。

2.2 结果与探讨

区域水环境污染是一个复杂的问题，在特定的时间和区域，河流水质受到很多因素的影响。其中主要因素有两个：①进入河流中污染物质的量，包括污染物的排放量和进入河流的污染物通量；②该区域河流水质中污染物的背景浓度及水质自净能力[8]。综合分析浐灞流域水系统特点、水资源构成及污染物的排放情况，可以进一步推断出浐灞流域地表水主要是受到灞河中游的农业生产与下游工业生产的双重影响。

1) 浐灞上游水质影响因素

浐河口属浐灞上游水域,其主要污染来自面源污染,包括农业污染和农村生活污水的排放，其中农业污染主要包括了农田污水与养殖业污水的排放。由于农业肥料的使用主要是以氮肥、磷肥为主，因此造成排入流域的农业废水中氮素与磷素含量超标，此外随意堆放生活垃圾，也导致了周围水体的污染[9]。在主成分分析法的结果中浐河口在主成分1中排名第一，表明其水质受到总氮、总磷、氨氮的影响最为严重，与实际分析结果相同。

2) 浐灞下游水质影响因素

浐灞流域下游是陕西省纺织工业、国防制造工业、汽车工业的重要生产地，生活污水和工业废水大量排入，让浐灞下游地表水环境受到严重污染。随着流域内上下游地区经济的高速发展，水环境污染有加剧的趋向[10]。从主成分分析法的结果来看，浐灞流域下游越靠近世园会与湿地公园的区域，水质情况明显好于三郎村等工业生产区域的水质，表明湿地生态处理系统起到了改善浐灞流域下游地表水质的作用。

3 结 语

目前使用主成分分析法进行水质分析的大部分研究人员，忽视了KMO和Bartlett的检验，直接进行数据的相关性分析，造成最终综合评价的偏差。而浐灞流域通过KMO和Bartlett检测，且分析结果符合实际情况，表明浐灞流域可以用主成分分析法进行流域污染情况的初步判断。

通过对2013年全年的浐灞流域水质指标进行主成分分析法分析及流域现状可以看出：浐河口处于浐灞流域上游，易受到农业污废水的影响，由于目前农业肥料以氮磷肥料为主，导致向浐河排放的污废水中总氮、总磷以及氨氮的指标过高；同时三郎村与浐灞交汇口均处于浐灞下游工业生产区域，根据对浐灞流域的水质评价表明，该区域水质长期处于劣Ⅴ类水，其中总氮超标9倍、氨氮超标7倍、总磷超标3.5倍。说明运用主成分分析法得出的水质评价结果与浐灞流域实际水质评价基本一致[9]。因此，可以通过主要成分的得分与综合得分概括性地描述2013年浐灞流域的水质主要特性，同时主成分分析法也证明了浐灞流域的污染特征具有鲜明的区域性，这对浐灞流域水环境有针对性地进行治理具有实际的参考意义。

参考文献:

[1] 王媛,王伟,徐锬，等.中国水环境压力与水污染防治能力的区域差异[J].环境科学与技术,2008,31(4):13-16.

Wang Yuan,Wang Wei,Xu Tan,et al.Water evironment pressure and capability of water pollution control:regional diversity in China[J].Environmental Science & Technology,2008,31(4):13-16.

[2] 徐志嫱,刘维.西安浐灞截污工程对水质改善的效果研究[J].西安理工大学学报,2011,27(1):18-23.

Xu Zhiqiang,Liu Wei.Research on improving effects of sewage interception on water quality of Chanba river in Xi'an[J].Journal of Xi’an Uniersity of Technology,2011,27(1):18-23.

[3] 徐志嫱,刘维,张建丰,等.基于流域不同特征的浐灞河生态系统健康评价[J].西北农林科技大学学报：自然科学版,2011,39(8):215-223.

Xu Zhiqiang,Liu Wei,Zhang Jianfeng,et al.Ecosystem health assessment based on the diffent characteristics of Chanba river basin,xi'an[J].Journal of Northwest A&F University(Nat.Sci.Ed),2011,39(8):215-223.

[4] 时立文.SPSS 19.0统计分析从入门到精通[M].北京:清华大学出版社,2012:286-287.

[5] 王晓鹏.河流水质综合评价之主成分分析方法[J].数理统计与管理,2001,20(4):49-52.

[6] 张亚娟,牛姗姗,孙亚乔,等.SPSS软件在渭河流域(陕西段)水质主成分分析评价中的运用[J].安徽农业科学,2012,40(29):14414-14416.

Zhang Yajuan,Niu Shanshan,Sun Yaqiao,et al.Application of SPSS in the principal component analysis of water quality in Weihe river[J].Journal of Anhui Sci,2012,40(29):14414-14416.

[7] 姚焕玫,黄仁涛,刘洋,等.主成分分析法在太湖水质富营养化评价中的应用[J].桂林工学院学报,2005,25(2):248-250.

[8] 魏善发.基于SPSS软件分析上海市金山区地表水污染特征[J].中国环境检测,2013,29(1):75-81.

Wei Shanfa.Based on SPSS software to analyze characteristics of surface water pollution,Jinshan District,Shanghai[J].Environmental Monitoring in China,2013,29(1):75-81.

[9] 周孝德,宋策,蔡剑,等. 西安浐灞河下游河段典型污染物水环境容量研究[R].2010.

[10] 孙旭,宋孝玉.西安市浐灞河流域水环境问题及治理措施[J].水资源与水工程学报,2009,20(5):44-48.

Sun Xu,Song Xiaoyu.Water environment problem and the control measures in Chanba River Basin of Xi’an[J].Journal of Water Resources & Water Engineering,2009,20(5):44-48.