基于HTI介质各向异性正演的裂缝预测属性优选

孙 炜,何治亮,李玉凤,周 雁

(1.中国石油化工股份有限公司石油勘探开发研究院构造与沉积储层实验室,北京100083;2.中国石油大学(北京),北京102249;3.中国石油化工股份有限公司胜利油田物探研究院,山东东营257022)

预测储层裂缝分布特征的最终目的是得到裂缝的发育程度和方向,从而指导后续的勘探开发工作。目前,基于纵波方位各向异性的裂缝预测方法是能够解决裂缝预测难题的技术手段之一。国内学者对此开展了较多的应用研究，如：曲寿利等[1]较早地论述了纵波方位各向异性裂缝预测在实际应用中的诸多技术细节;乐绍东[2]利用纵波方位各向异性裂缝检测技术较为准确地预测了川西坳陷上三叠统须家河组的裂缝分布特征;喻岳钰等[3]利用瞬时频域衰减属性的方位各向异性,在碳酸盐岩裂缝预测中取得成功;姜传金等[4]基于纵波阻抗、频率衰减的方位各向异性信息,准确预测了松辽盆地北部徐家围子断陷营城组火山岩的裂缝发育情况。此外,尹志恒等[5]和刘振峰等[6]等对国内外纵波方位各向异性裂缝预测的科研实践做了详细的调研。总体来看,纵波方位各向异性裂缝预测技术在不同岩性地层的裂缝预测研究中得到越来越广泛的应用[7-8]。

前人应用研究成果表明,利用纵波方位各向异性预测裂缝的发育特征是行之有效的。但是,在选取用于各向异性椭圆拟合的地震属性时,研究人员往往采用两种思路:一是经验性的地震属性优选;二是计算出若干种地震属性数据体,分别进行各向异性椭圆拟合并求取出裂缝分布特征,再通过对比各种计算结果与测井裂缝信息的吻合度来确定合适的地震属性。这两种方法中,第一种方法带有人为主观因素,第二种方法则会极大地增加科研工作量。那么,如何合理、简便、有效地进行地震属性优选,成为影响方法应用效果的实际问题。

在地震储层预测研究中,人们经常通过正演模拟的方式来确定对储层最为敏感的地震属性。相似地,针对裂缝的各向异性正演应当也同样可以进行裂缝敏感属性的优选。但是,目前将各向异性正演与方位各向异性裂缝预测方法相结合的已发表文献尚不多见。

我们将各向异性正演引入方位各向异性裂缝预测中,解决该方法在实际应用中的地震属性优选问题。首先,结合测井、试油信息进行基于HTI介质的正演模拟,得到含有方位各向异性信息的井旁地震道集;然后,对正演地震道集进行多种地震属性的计算和裂缝敏感性分析;最后,将优选出的最佳敏感属性用于各向异性椭圆拟合和研究区储层的裂缝预测。实际数据的应用试验结果表明,基于HTI介质的各向异性正演能够有效指导用于各向异性椭圆拟合的地震属性优选,优化方位各向异性裂缝预测方法的应用过程。

1 原理及思路

1.1 方位各向异性裂缝预测原理

地层重力压实作用的存在,使高角度裂缝比低角度裂缝更容易保存下来,同时,高角度裂缝对裂缝型油气藏的贡献也远远大于低角度裂缝。因此,与表征高角度裂缝的HTI介质的相关研究就变得意义重大。Ruger[9-11]在HTI介质Thomsen系数的基础上,得到图1所示模型中纵波速度以及反射系数随方位角和入射角变化的公式:

(1)

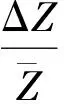
图1 Ruger[9-11]的公式(1)对应的地质模型

当入射角较小时,(1)式中的最后一项可以略去。略去最后一项并令

(2)

则(1)式变为

(3)

式中:Biso为各向同性项;Bani为各向异性项。

当地震数据包含3个或3个以上不同入射角、方位角振幅信息时,结合子波可以得到对应的不同入射角、方位角的反射系数。此时,通过求解超定方程组可以得到Biso和Bani,然后利用Biso和Bani这两项实现方位各向异性椭圆的拟合。Mallick等[12]认为,由各向同性项和各向异性项拟合出来的椭圆可以用来表征裂缝的发育特征,裂缝的发育程度由拟合椭圆的长、短轴之比来量化,裂缝的方向则由椭圆的长轴或短轴予以指示。

1.2 各向异性正演原理

裂缝的地震特性受裂缝的倾角、开度、延伸和充填物等众多因素影响。因此,当岩石含裂缝后其物理特性将变得更为复杂,选择合适的等效介质模型是进行各向异性正演的基础。目前,关于裂缝的等效介质模型有Hudson模型[13]、Thomsen模型[14]以及Eshelby-Cheng模型[15]。本文各向异性正演选用的是Hudson模型,通过对含有薄硬币状的椭球缝隙或包含物的弹性固体中的平均波长的散射理论分析得到。其模型基于如下假设[16]:①从形状上,理想化的裂隙形状为硬币状,即高宽比要小,裂隙彼此之间是隔离的,隙间不存在流体流动;②介质包含裂隙半径及缝隙间距远小于地震波长的定向疏排列裂隙;③裂缝包体内所含气体、液体或其它物质的体积模量和剪切模量比围体的小。

其等效的刚度系数为

(4)

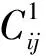
(5)

式中:V为介质基质的体积;N为体积V内的裂缝总数,即体密度;a为裂缝半径;φ为裂缝孔隙度;α为裂缝扁率(纵横比)。

1.3 各向异性正演的思路与过程

由于各向异性正演提供了裂缝在井旁地震道的地震响应,包括叠前各方位角的AVO特征及在裂缝影响下的AVO特征随方位角的变化规律,因此,它可以为纵波方位各向异性裂缝分布特征预测提供基础信息。由正演模拟得到的地震合成记录获得振幅、频率和相位等叠前地震动力学属性,通过计算这些动力学属性对于裂缝的敏感性,可以简便、有效地实现各向异性椭圆拟合的地震属性优选。图2给出了本文各向异性正演的研究思路。

图2 各向异性正演研究思路

基于HTI介质Hudson模型各向异性正演过程为:假设在井口布置如图3所示的观测系统,通过测井资料得到岩石的纵波速度、横波速度和密度,在给出裂缝所含流体性质及对应弹性模量的情况下,确定出Hudson等效介质模型的刚度系数及对应的各向异性系数;再根据Ruger的公式(1)计算出与入射角、方位角有关的反射系数;最后,通过与测井标定子波的褶积,得到不同入射角、方位角的地震波振幅信息。

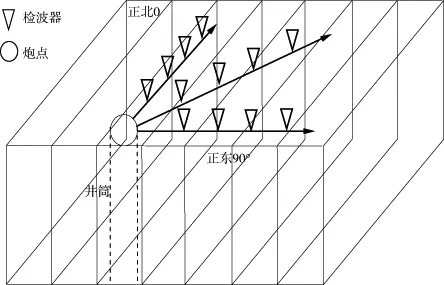
图3 各向异性正演模拟观测系统图示

2 实际应用试验

2.1 研究区地质背景

研究区位于松辽盆地南部北端某地区,目的层为白垩系营城组火山岩,地层厚度变化较大(钻井显示目的层厚度为350～900m)。区内最早的探井为A井,于2007年开钻,并于同年在营城组目的层火山岩进行试油,使用50.8mm油嘴获产天然气592m3/d,水62m3/d。一年后,在A井附近部署了另外一口探井B,在相近目的层使用12mm油嘴获天然气产量20.2464×104m3/d,展现了该地区良好的勘探潜力。

根据钻井资料分析,研究区火山岩储层由孔、洞、缝组成,裂缝类型主要包括构造缝和成岩缝,裂缝是保持该地区储层连通性和流体运移的主要通道。如何利用地震数据准确有效地预测该地区火山岩裂缝的分布特征是亟待解决的问题。

2.2 正演井段选取

为了检验用各向异性正演分析裂缝方位各向异性方法的有效性,需要选取合理的正演参数来分析不同流体和不同裂缝密度情况下的地层方位各向异性情况,并计算多种地震属性,分析各种地震属性的裂缝敏感性,从而指导后续的叠前方位各向异性裂缝预测。

研究区内有4口钻井,分别为A,B,C,D井,其中A井和B井资料较为完全,且有FMI(地层微电阻率成像)测井资料。根据对FMI裂缝测井资料和试油结果的综合分析,选取A井的3个井段(自上而下依次命名为A1,A2,A3,其FMI井壁图像见图4)进行各向异性正演,具体参数见表1。由表1 可以看出,所选井段的FMI裂缝密度、试气结果均有一定差异,可以进行正演模拟结果的对比分析。

图4 各向异性正演所选取A1，A2和A3井段的FMI井壁图像

表1 各向异性正演选取井段参数及试气结果

2.3 多属性敏感性分析优选

在储层预测研究中,叠后地震属性是一种较常规的预测储层及流体分布特征的技术手段。在火山岩地层中,流体及裂缝易引起地震数据的频谱发生变化,本次研究选取的属性为与地震频谱相关的一类属性,主要包括总能量、最大能量、65%衰减频率、85%衰减频率、35Hz能量比、起始衰减频率和相对波阻抗等7种地震属性。

研究中,首先利用正演出的道集在给定时窗内分别计算上述7种地震属性,并将计算出的数据导出为ASCII格式;然后以方位角0,入射角0时的属性值为参考基准值,针对所选取的A1,A2和A3 3个井段,结合矩阵实验室(Matlab)三维成图,分析各地震属性在入射角0≤θ≤30°,方位角0≤φ≤90°对裂缝的敏感性,如图5至图8所示。通过对A1井段(无裂缝无流体)、A2井段(裂缝发育、高产气层)和A3井段(裂缝发育、气水同层)各地震属性的敏感性分析和结果对比,寻找最适合进行各向异性椭圆拟合的地震属性。

综合对比图5至图8中7种属性的裂缝敏感性分析结果,得出以下结论。

图5 正演模拟道集所计算能量类地震属性的裂缝敏感性分析a 总能量属性; b 最大能量属性

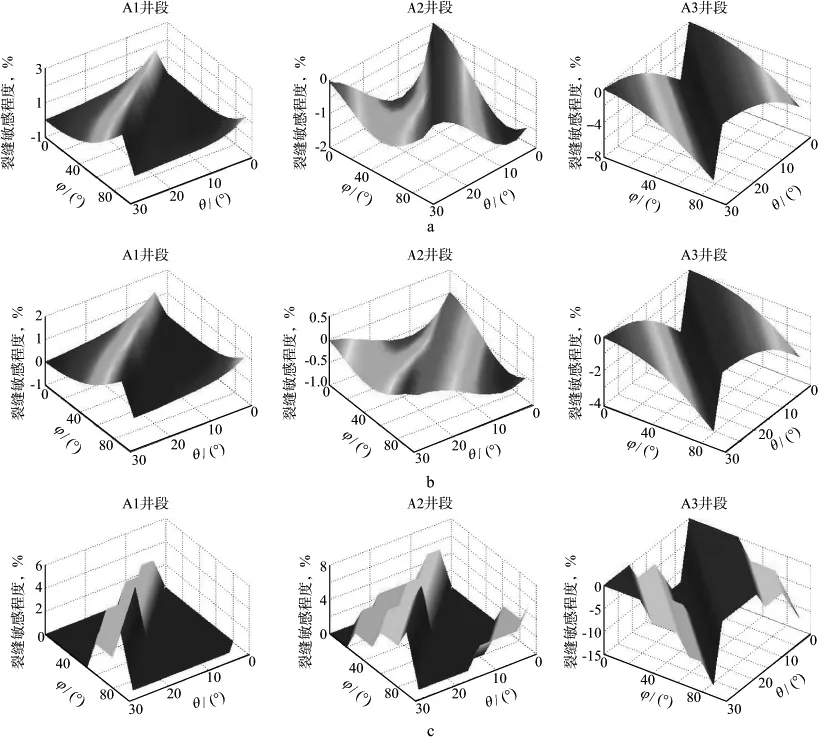
图6 正演模拟道集所计算频率类地震属性的裂缝敏感性分析a 65%衰减对应频率属性; b 85%衰减对应频率属性; c 起始衰减频率属性

图7 正演模拟道集所计算相对波阻抗属性的裂缝敏感性分析

图8 正演模拟道集所计算35Hz低频能量比属性的裂缝敏感性分析

1) 能量类地震属性(图5)在A1,A2井段表现为明显的负异常,但在A3井段却表现为正异常。由于A1井段无裂缝,而A2井段裂缝发育,那么利用该类地震属性无法区分裂缝是否发育。因此,能量类地震属性不适用于本区各向异性椭圆拟合的裂缝预测。

2) 在频率类属性(图6)中,百分比衰减对应频率属性(图6a和图6b)在A1井段为幅值不大的正异常,在A2井段为幅值不大的负异常,在A3井段为幅值略大的负异常。该类属性在A1,A2和A3井段的值有一定差异,但幅值变化不够明显,在地震数据信噪比不高时,无法保证计算结果的准确性。而起始衰减频率属性(图6c)在A1,A2井段表现为正异常,在A3井段为负异常,也不适用于区分裂缝是否发育。

3) 相对波阻抗属性(图7)在A2井段表现为较高的正异常,在A1井段为中等正异常,在A3井段为较低正异常。该属性在不同裂缝发育程度、不同流体性质的地层存在一定区分性。

4) 低频能量比属性(图8)在裂缝含气井段A2表现为较高的正异常,在裂缝气水同层井段A3表现为中等正异常,在无裂缝干层井段A1表现为低的正异常甚至负异常。该属性对不同井段展现出的这种区分程度非常有利于进行研究区各向异性椭圆的拟合。

根据以上分析结果可知,低频能量比属性是研究区裂缝预测的最敏感属性。优选低频能量比属性进行研究区各向异性椭圆的拟合,预测裂缝的平面分布特征。

2.4 利用优选属性预测裂缝分布特征

利用正演模拟不同方位角道集计算的低频能量比属性进行各向异性椭圆的拟合,根据拟合椭圆的长、短轴之比得到了研究区营城组裂缝的空间分布预测结果。基于井上裂缝信息,分别从剖面和平面上探讨本文方法预测的研究区裂缝分布特征。

图9给出了低频能量比属性方位各向异性预测的过A井和B井目的层段裂缝密度剖面(图中色标为各向异性椭圆的长、短轴之比,即各向异性强度值;无量纲),可以看出,在A井试气段和B井产气段预测的裂缝密度均为高值。可见利用低频能量比属性各向异性预测的裂缝发育情况不仅与FMI测井资料吻合较好,也符合井上已知的地质认识。

研究区内发育若干条南北走向的断层。从预测的裂缝平面分布特征(图10)来看,研究区营二段、营三段和营四段(T4a至T4c)裂缝方向以近南北向为主,北东—南西向为辅(图10a),营一段(T4c至T41)裂缝方向以南北向为主,东西向为辅(图10b),裂缝方向与断层走向较为相似(玫瑰图中色标代表某一方向的裂缝占该位置目的层段所有裂缝方向的百分比，红色指示预测出的裂缝优势方向)。预测的裂缝发育区主要分布在断层附近,同时在断层周边存在若干成岩缝发育带。对于有FMI资料的A井和B井,在T4a-T4c层段,A井和B井裂缝均发育;在T4c-T41层段,A井裂缝发育而B井裂缝不发育。从裂缝分布特征(图10)来看,本文方法预测结果与单井的裂缝发育情况较为一致。

图9 低频能量比属性方位各向异性预测的过A井和B井目的层段裂缝密度剖面

图10 低频能量比属性方位各向异性预测的不同层段裂缝平面分布a T4a-T4c层段; b T4c-T41层段

将预测结果与FMI解释结果进行对比,进一步验证本文方法的有效性。图11给出了FMI裂缝方向(图11a，图11b，图11c)与低频能量比属性方位各向异性预测的A井裂缝方向(图11d)的对比结果(白底玫瑰图为FMI裂缝方向,黑底玫瑰图为预测方向)。从图11中可以看出,预测的A井裂缝方向几乎为FMI测井资料显示的多种裂缝类型裂缝方向的综合显示(B井的对比结果也相似),说明本文方法预测的裂缝方向较为可信。

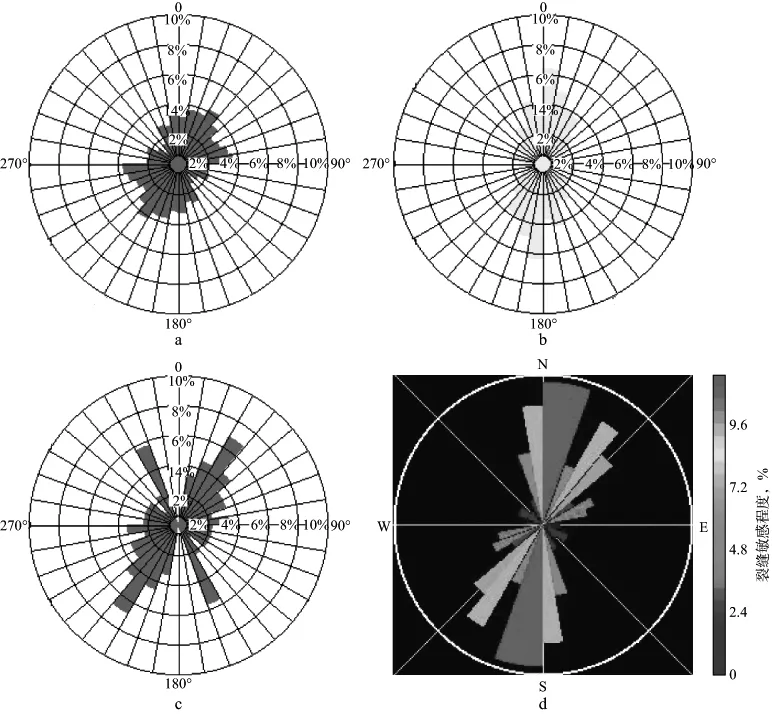
图11 低频能量比属性方位各向异性预测的A井裂缝方向与FMI对比a 高导缝的走向为北东—南西向; b 高阻缝的走向为南北向; c 微裂缝的走向为北东—南西向; d 本文方法预测的A井裂缝方向

3 结论与认识

各向异性椭圆拟合是纵波方位各向异性裂缝预测方法中重要的一步,其关键在于如何合理有效地进行地震属性的优选。我们提出了利用各向异性正演进行方位各向异性椭圆拟合地震属性优选的新思路。通过基于HTI介质Hudson模型的正演模拟得到含有各向异性信息的井旁地震道集,并对地震道集进行多种地震属性的计算,对比分析各地震属性的裂缝敏感性,从而优选出最适合进行方位各向异性椭圆拟合的地震属性。松辽盆地南部某地区白垩系营城组火山岩储层的实际应用试验取得了较好的裂缝预测效果,并得到以下认识。

1) 能量类地震属性、频率类属性和相对波阻抗属性不适用于研究区各向异性椭圆拟合的裂缝预测,低频能量比是进行该地区各向异性椭圆拟合的优选敏感属性。但这一结果并不具有普遍性,在不同地区对不同储层进行各向异性正演时,地震属性的优选结果也会不同。

2) 研究区裂缝分布特征与断层展布较为一致,营二段、营三段和营四段裂缝方向为以近南北向为主,北东—南西向为辅;营一段裂缝方向为南北向为主,东西向为辅。此外,预测的裂缝分布特征在单井FMI资料上得到了较好的验证。

3) 多属性裂缝敏感性分析是基于Hudson模型的高角度裂缝,但以低角度裂缝、水平裂缝为主的储层是客观存在的,在面对这一类储层的裂缝预测问题时,文中涉及的多属性裂缝敏感性分析技术不适用。

致谢:在本文编写过程中得到中国地质大学(北京)王彦春教授、刘学清博士和刘志伟博士的指导和启发,在此表示衷心感谢！

参 考 文 献

[1] 曲寿利,季玉新,王鑫,等.全方位P波属性裂缝检测方法研究[J].石油地球物理勘探,2001,36(4):390-397

Qu S L,Ji Y X,Wang X,et al.Seismic method fro using full-azimuth P-wave attributes to detect fracture [J].Oil Geophysical Prospecting,2001,36(4):390-397

[2] 乐绍东.AVA裂缝检测技术在川西JM构造的应用[J].天然气工业,2004,24(4):22-24

Yue S D.Application of AVA fracture detection technique in JM structure in west Sichuan [J].Natural gas industry,2004,24(4):22-24

[3] 喻岳钰,杨长春,王彦飞,等.瞬时频域衰减属性及其在碳酸盐岩裂缝检测中的应用[J].地球物理学进展,2009,24(5):1717-1722

Yu Y Y,Yang C C,Wang Y F,et al.P-wave azimuthal attenuation attributes in wavelet-scale domain and its application to fracture detection in carbonate [J].Progress in Geophysics,2009,24(5):1717-1722

[4] 姜传金,鞠林波,张广颖,等.利用地震叠前数据预测火山岩裂缝的方法和效果分析——以松辽盆地北部徐家围子断陷营城组火山岩为例[J].地球物理学报,2011,54(2):515-523

Jiang C J,Ju L B,Zhang G Y,et al.The method and effect analysis of volcanic fracture prediction with prestack seismic data——an example from the volcanic rocks of Yingcheng formation in Xujiaweizi fault depression,north of Songliao Basin [J].Chinese Journal of Geophysics,2011,54(2):515-523

[5] 尹志恒,狄帮让,李向阳,等.国外应用纵波各向异性技术检测裂缝的研究进展[J].科技导报,2011,29(30):73-78

Yin Z H,Di B R,Li X Y,et al.Progress in P-wave anisotropy technology for fracture detection [J].Science and Technology Review,2011,29(30):73-78

[6] 刘振峰,曲寿利,孙建国.地震裂缝预测技术研究进展[J].石油物探,2012,51(2):191-198

Liu Z F,Qu S L,Sun J G.Progress of seismic fracture characterization technology[J].Geophysical Prospecting for Petroleum,2012,51(2):191-198

[7] 孙炜,王彦春,李梅,等.利用叠前地震数据预测火山岩储层裂缝[J].物探与化探,2010,34(2):229-232

Sun W,Wang Y C,Li M,et al.The detection of fractures in volcanic reservoir with pre-stack seismic data [J].Geophysical and Geochemical Exploration,2010,34(2):229-232

[8] 孙炜,李玉凤,何巍巍,等.P波各向异性裂缝预测技术在ZY区碳酸盐储层中的应用[J].石油与天然气地质,2013,34(2):137-144

Sun W,Li Y F,He W W,et al.Sun Using P-wave azimutal anisotropy to predict fractures in carbonate reservoirs of the ZY block[J].Oil & Gas Geology,2013,34(2):137-144

[9] Ruger A.Reflection coefficients and azimuthal AVO analysis in anisotropic media[D].Colorado:Colorado School of Mines,1996

[10] Ruger A.P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry [J].Geophysics,1997,62(3):713-722

[11] Ruger A.Using AVO for fracture detection:analytic basis and practical solutions [J].The Leading Edge,1997,16(10):1429-1430,1432-1434

[12] Mallick S,Craft K L,Meister L,et al.Determination of the principle direction of azimuthal anisotropy from P-wave seismic data [J].Geophysics,1998,63(2):692-706

[13] Hudson J A.Wave speeds and attenuation of elastic waves in material containing cracks[J].Geophysical Journal of the Royal Astronomical Society,1981,64:133-150

[14] Thomsen L.Elastic anisotropy due to aligned cracks in porous rock[J].Geophysical Prospecting,1995,43(6):805-829

[15] Cheng C H.Crack models for a transversely anisotropic medium[J].Journal of Geophysical Research,1993,98:675-684

[16] 葛瑞·马沃可,塔潘·木克基,杰克·徳沃金.岩石物理手册:孔隙介质中地震分析工具[M].徐海滨,戴建春，译.合肥:中国科学技术大学出版社,2008:113-118

Mavko G,Mukerji T,Dvorikin J.The rock physics handbook:tools for seismic analysis in porous media[M].Xu H B, Dai J C,translators.Hefei:University of Science and Technology of China Press,2008:113-118

[17] Crampin S.Effective anisotropic elastic constants for wave propagation through cracked solids[J].Geophysical Journal of the Royal Astronomical Society,1984,76(1):135-145