一种基于相似系数谱约束的多次波自适应减去方法

孙维蔷,王华忠,胡江涛

(同济大学海洋与地球科学学院波现象与反演成像研究组,上海200092)

多次波处理的核心是多次波的预测、分离和成像应用,目前已逐渐向多次波的成像应用方面转移。将多次波作为噪声进行压制是工业界较认可的一种途径,其中将多次波压制分为预测和减去两步进行的思路最受关注[1-3]。多次波压制方法主要分为两类[4-6]:滤波类和波动方程类。

基于信号处理的滤波类方法,主要是根据多次波与一次波之间周期性和动校速度等差异特征进行多次波压制。如预测反褶积[7]是基于多次波的周期性和一次波的非周期性来压制水体鸣震等周期性多次波。对于近偏移距数据,预测反褶积的多次波周期性假设能得到较好满足,但对于大偏移距数据,通常需要在τ-p域重构多次波的周期性,再通过τ-p域预测反褶积来实现多次波的压制。共中心点叠加通过一次波的同相叠加和多次波的非同相叠加实现部分多次波的压制。F-K滤波法[8]和Radon变换法[9]根据多次波和一次波的视速度差异在变换域中压制多次波。由于多次波和一次波的视速度差异在远偏移距处较为明显,因此,基于视速度差异的滤波类方法对远偏移距数据的多次波压制效果较好,对近偏移距数据的多次波压制则较为困难。聚束滤波方法[10]根据一次波和多次波的动校正量、振幅及相位随偏移距的变化差异来设计聚束滤波器,应用聚束滤波器来衰减多次波。总之,滤波类方法在多次波和一次波特征具有明显的差异时,能较好地压制多次波;当多次波和一次波特征差异不明显时,用滤波类方法压制多次波很困难。

波动方程类多次波压制方法主要是基于波动方程预测多次波模型,将原始记录与多次波模型进行匹配相减,实现多次波的预测和减去。波动方程类方法对多次波模型的预测主要分为模型驱动和数据驱动两种途径。模型驱动类预测方法,如波场外推法[1],是基于模型的先验信息,利用波动方程进行波场外推,预测出多次波模型。由于水体模型较容易获取,因此波场外推法通常用来预测水体相关多次波。数据驱动类预测方法则直接根据原始数据来预测多次波模型,不需要先验信息。反馈环法[3]和逆散射级数法[11]是两种经典的数据驱动类多次波模型预测方法:反馈环法主要针对自由表面多次波模型;逆散射级数法是基于散射级数理论的多次波模型预测方法,理论上可以预测所有类型的多次波模型。我们采用的多次波模型预测方法是反馈环法,只考虑自由表面多次波的自适应减去问题,层间多次波的减去问题与此类似。

由波动方程类方法预测出的多次波模型可以较准确地预测多次波旅行时,但振幅和相位与真实多次波存在差异,需要将原始记录中的多次波与多次波模型进行匹配,从原始记录中减去多次波。多次波的减去通常被看作是最小二乘意义下的数据匹配问题[12],即以原始数据和多次波模型之间的能量差最小(即一次波能量最小)为准则,进行多次波的剔除,通常由单道或多道维纳滤波来实现。基于L2范数的单道维纳滤波容易实现,且速度快,但由于L2范数本身存在两点假设,一是要求一次波与多次波正交(即两者的内积为0),二是由于L2范数对野值较敏感,因此要求一次波相对于多次波能量较小。只有当这两点假设条件都很好地得到满足时,基于L2范数的自适应减去才能取得较好的效果。

在常规自适应减去只进行振幅匹配的基础上,伪多道滤波[13-15]方法通过Hilbert变换,引入数学衍生道,同时进行旅行时和相位属性的匹配,改善了波形匹配的效果。预测误差滤波及模式识别类方法[16]利用了包含道间相移和横向振幅变化的空间向量,从原始记录和预测多次波模型中提取多次波同相轴。独立分量分析[17]方法将多次波自适应减去看作“盲源分离问题”,假设一次波和多次波相互独立,利用高阶统计量来度量两者的独立性,从而进行分离。这些方法部分突破了L2范数的正交性假设。考虑到L1范数对野值不敏感的特点,可以用L1范数代替L2范数作为减去准则[4],从而避免L2范数要求一次波具有最小能量的假设。

另一方面,相对于时域,τ-p域或Radon域中一次波与多次波之间的正交性更明显。因此当一次波与多次波非正交时,在变换域中进行多次波自适应减去的效果会更好。考虑到当时距曲线不满足双曲假设时,局部τ-p变换较全局τ-p变换或者Radon变换能更好地提取信号的线性特征,因此,我们在局部τ-p域中进行多次波的自适应减去。由于传统的局部τ-p变换存在分辨率低的问题,我们用基于Radon谱约束的最小二乘反演方法来实现正/反局部τ-p变换。Radon谱作为先验信息能有效地改善反演解的倾向性,同时可以作为正则化算子来提高反问题求解的稳定性。另外,由于Radon谱是通过局部叠加实现的,对随机噪声也有一定的压制作用。在局部τ-p域,我们用预测多次波模型的相似系数谱来指示原始记录中多次波存在的位置,设计滤波器,同时实现预测多次波模型与原始记录中多次波的振幅、相位和旅行时匹配,自适应地减去多次波。

1 高分辨率局部τ-p变换

1.1 正问题

高精度的局部平面波数据,可以通过建立局部平面波数据的预测方程,求解反问题得到。首先需要研究相应的局部平面波传播的正过程。局部平面波束形成的正过程可以在时间-空间域表示,也可以在频率-空间域表示。时间-空间域描述正过程的好处是反演时便于在时间和射线参数两个方向上加入稀疏约束,但是计算效率较低。频率-空间域正过程由于并行计算效率高且便于在射线参数方向上加入稀疏约束等特点而得到广泛应用。

在频率-空间域,单频的空间局部数据可以由数据矩阵表示，即

(1)

其中,m为道数。局部平面波源可以表示为

(2)

其中,n为射线参数的个数。时移矩阵可以表示为

(3)

式中:ω为圆频率;p为射线参数;x0为参考道的位置,通常取中心道的位置。时移矩阵中每一列代表一个方向的局部平面波传播的相位移。空间局部的数据可以理解为局部平面波源经过时移矩阵作用并在各局部空间点叠加产生的结果。因此,对于不同的频率,正问题可以描述为

(4)

1.2 反问题

从反演的角度来理解局部正τ-p变换,反问题可以描述为已知局部数据和时移矩阵，求解局部平面波源的过程。通过最小化如下目标泛函来估计局部平面波源:

(5)

其中,λ为权系数。最小二乘意义下,该泛函的解可表示为

(6)

将Hessian矩阵的逆矩阵项(AHA+λI)-1忽略,可得到近似解：

(7)

该近似解就是常规局部正τ-p变换的结果。由于时移矩阵A不是正交矩阵,所以AHA不等于单位矩阵,说明局部τ-p变换结果存在泄漏噪声和低分辨率问题。为了得到高分辨率的结果,Hessian矩阵的逆矩阵项不能被忽略。但最小二乘解同样受到泄漏噪声问题的困扰,可以通过加入先验信息约束来改善。

1.3 Radon谱约束的高分辨率局部τ-p变换

将线性Radon变换结果Sa作为最小二乘反演的初始值,虽然受到泄漏噪声和低分辨率的影响,但它的能量仍然能够反映有效局部平面波源的可能性。能量越大,为有效射线束的可能性就越大;能量越小,为泄漏噪声的可能性就越大。用于约束的能量计算公式为

(8)

式中:ω1,ω2为有效频带的起始和终止频率;i=1,2,…,np。在实际计算时,需要将该能量归一化到0～1。该约束因子对随机噪声不敏感,因此,随机噪声对该因子约束反演的结果影响小。通常,局部地震数据仅包含少数几个射线参数,因此该能量也是一条比较稀疏的曲线。

Radon谱能量约束下局部平面波反演的目标函数可以写为

(9)

其中R为np×np的对角矩阵,其对角线上的元素为

(10)

其中,ε取一个很小的数来使数值计算稳定。

(9)式的最小二乘解为

(11)

通过上述L2范数下的反问题求解,可以得到高精度的局部平面波的估计。进一步地,还可以利用各种范数下的目标泛函来实现更稀疏化的局部平面波分解。

2 局部τ-p域基于相似系数谱约束的多次波自适应减去方法

多次波减去阶段的主要任务是将预测多次波的振幅和相位等属性与原始数据中的真实多次波相匹配。因此,将多次波的自适应减去看作是最小二乘意义下的数据匹配问题的思路被广为接受。匹配过程可以表示为

(12)

式中:p(t)为一次波;y(t)为原始数据;mj(t)和fj(t)分别为第j道的预测多次波模型和匹配滤波器;N为用于匹配的道数,即N=1对应的是单道匹配,N>1对应的是多道匹配。

最小二乘意义下,求取匹配算子fj(t):

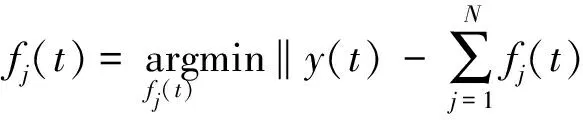
(13) 常规自适应减去过程是通过求解方程(13)来完成匹配的。考虑到L2范数本身存在的限制,即要求预测多次波模型与一次波正交且一次波能量最小；在τ-p域,多次波和一次波分离得更明显,可以部分解决时域匹配时由于两者非正交而引起的问题；相对于全局τ-p域,在局部τ-p域,多次波与一次波的正交性可以进一步被改善。因此,基于Radon谱约束的高分辨率局部τ-p变换是这种多次波自适应减去方法的基础。在利用局部τ-p域转换使多次波和一次波正交性有所改善的基础上,我们基于预测多次波的旅行时相对准确这一假设,利用预测多次波的相似系数谱来确定原始相似系数谱中多次波存在的位置,设计简单的滤波器(如Butterworth类滤波器)对原始数据进行滤波,从而实现多次波的自适应减去。相似系数谱可以定义为沿着某一轨迹上的输出与输入能量之比[18-19]。

二维相似系数谱的定义为

(14)

其中,d(τ,x)为数据道,τ和x分别表示截距时间和空间位置;L和W分别表示局部窗的空间道数和时间方向上的长度。相似系数的分母项的作用是对振幅进行归一化,使相似系数的值与振幅无关,降低振幅匹配的难度,使其不再需要在维纳滤波框架下通过求解线性方程组来实现振幅匹配,而是由预测多次波模型的相似系数谱作为约束,设计滤波器对原始数据进行滤波,直接实现多次波的减去。分子项相当于上述轨迹上的子波的包络,可以弱化子波变化对减去过程的影响,保证相位和旅行时等属性的有效匹配。这两个优点可以保证新减去方法比常规减去方法更有效、更稳定。

在局部τ-p域,当一次波和多次波在相似系数谱中正交时,可以根据多次波模型相似系数谱确定的多次波存在的位置设置阈值,对原始数据进行滤波,直接进行多次波的自适应减去。滤波器公式如下:

(15)

式中,λ为阈值。然而,即使在局部τ-p域中,多次波和一次波也很难完全正交。当两者非正交时,用(13)式进行直接滤波不能有效地保存一次波能量,因此,我们采用Butterworth类滤波器进行多次波的自适应减去。Butterworth类滤波器可以定义为

(16)

式中:Sm(τ,p)和Sd(τ,p)分别表示预测多次波模型和原始数据的相似系数谱;n是控制滤波器光滑程度的参数,通常是不大于10的偶数;ε是多次波压制参数。当多次波与一次波正交时,无论ε取值多少,Butterworth类滤波器都可以完全压制多次波;当两者非正交时,ε起到权系数的作用,根据多次波和一次波的正交情况来确定ε的取值。ε取值较大时,压制程度较小;反之,压制程度则较大。数值实验表明,ε≈0.1时,自适应减去的效果较好,此时,局部τ-p域的多次波自适应减去过程可以表示为

(17)

上述新减去方法除了能降低振幅匹配的难度,有效、稳定地进行多次波和一次波非正交情况下的多次波自适应减去之外,还可以减弱子波变化对匹配过程的影响,相当于在振幅匹配的同时,进行相位和旅行时匹配。原始数据与预测多次波模型中的子波不一致性,会导致预测多次波模型的相似系数谱无法准确地指示多次波存在的位置。当预测模型的相似系数谱所指示的多次波要多于真实存在的多次波时,通过上述滤波方法可以将多次波有效地减去;反之,上述方法则会产生残余的多次波。我们采取的解决方法是对含有残余多次波的相似系数谱进行平滑,平滑的结果中对应于一次波部分的相似系数值较大,而对应于残余多次波部分的相似系数值则较小,再设置阈值进行滤波,将残余的多次波进一步压制。

3 模拟数据测试和实际资料应用

3.1 合成记录数据测试

首先由主频为30Hz的雷克子波合成记录来证明新减去方法的有效性及优点,如图1所示。其中,图1a为原始数据；图1b为预测多次波模型,其振幅值为原始数据中真实多次波的2倍；图1c为真实一次波。图2为应用新减去方法的结果,其中

图1 主频30Hz雷克子波合成记录a 原始数据; b 预测多次波模型; c 真实一次波

左边为真实一次波,中间是减去结果,右边是两者做差结果。从图2中可以看出,当一次波与多次波非正交时,新减去方法可以有效地将真实多次波与多次波模型进行振幅匹配,实现多次波的自适应减去。图3是将图2中的预测多次波模型中雷克子波的主频由30Hz变为20Hz,应用新减去方法得到的结果。此时,预测多次波模型中的子波与原始子波不一致,导致预测多次波与真实多次波的振幅、旅行时和相位信息都出现误差,使得预测多次波模型的相似系数谱不能完全准确地指示真实多次波存在的位置。由图3可以看出,新方法仍可以有效地进行多次波减去,证明新减去方法不但可以进行振幅匹配,还可以进行相位和旅行时匹配,弱化子波变化对匹配相减过程的影响。图4为相似系数谱,其中图4a是对应于图1a中红框所示范围主频为30Hz原始数据的相似系数谱,图4b为对应于相同位置、主频为20Hz的预测多次波模型的相似系数谱,图4c为经过Butterworth类滤波器滤波后的相似系数谱,即用于局部τ-p域多次波自适应减去的滤波器。从图4可以看出,本文提出的新减去方法可以完全实现多次波的压制。

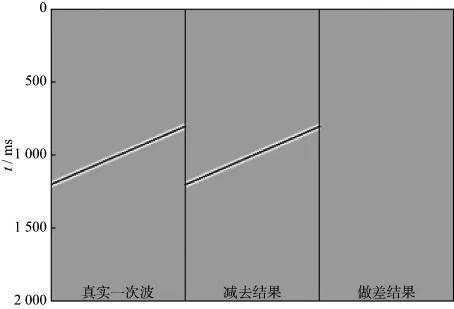
图2 主频为30Hz合成原始数据的多次波

图3 预测多次波模型中雷克子波主频由30Hz 变为20Hz 的多次波减去结果

3.2 模拟单炮记录测试

采用如图5所示的模拟单炮记录测试了新减去方法的有效性和稳定性。其中,图5a为原始单炮记录,图5b为反馈环法预测的自由表面多次波模型。比较图5a和5b可以发现,预测多次波模型中的多次波旅行时信息基本准确。图5c为应用本文新减去方法的结果,其中多次波已被完全减去。图5d至图5f是分别对应图5a至图5c中黄框内区域的放大图,比较图5d至图5f可见,本文方法可以很好地处理多次波和一次波非正交情况下的多次波减去。图6为用于约束的相似系数谱,其中图6a 和图6b分别为图5a和图5b中红框所示区域的原始数据和预测多次波模型的相似系数谱,图6c 为经过Butterworth滤波后的相似系数谱。从红框所示区域可以看出有残余的多次波存在,这是由于预测多次波模型与原始数据中的子波不一致所导致的,预测多次波相似系数谱所指示的多次波要少于真实存在的多次波。对图6c中的相似系数谱进行平滑,通过设置阈值进一步滤波,得到多次波自适应减去的滤波结果,如图6d所示。比较图6a 至图6d发现,多次波已经被完全压制。

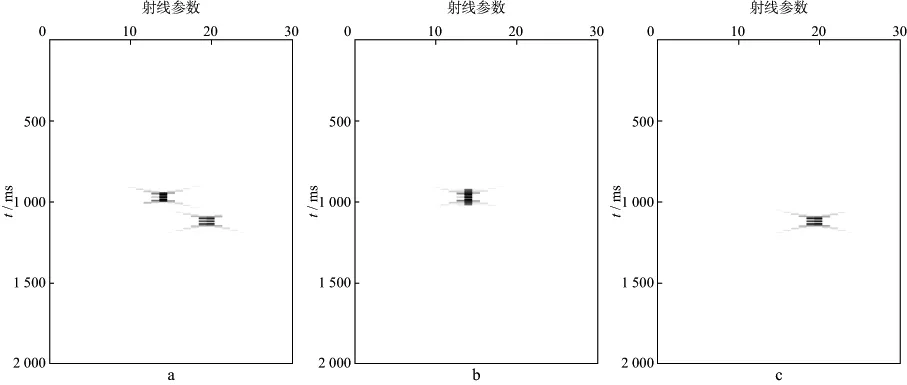
图4 主频30Hz雷克子波合成记录中红框所示范围内数据的相似系数谱a 原始数据; b 预测多次波模型; c 本文方法Butterworth滤波后的相似系数谱

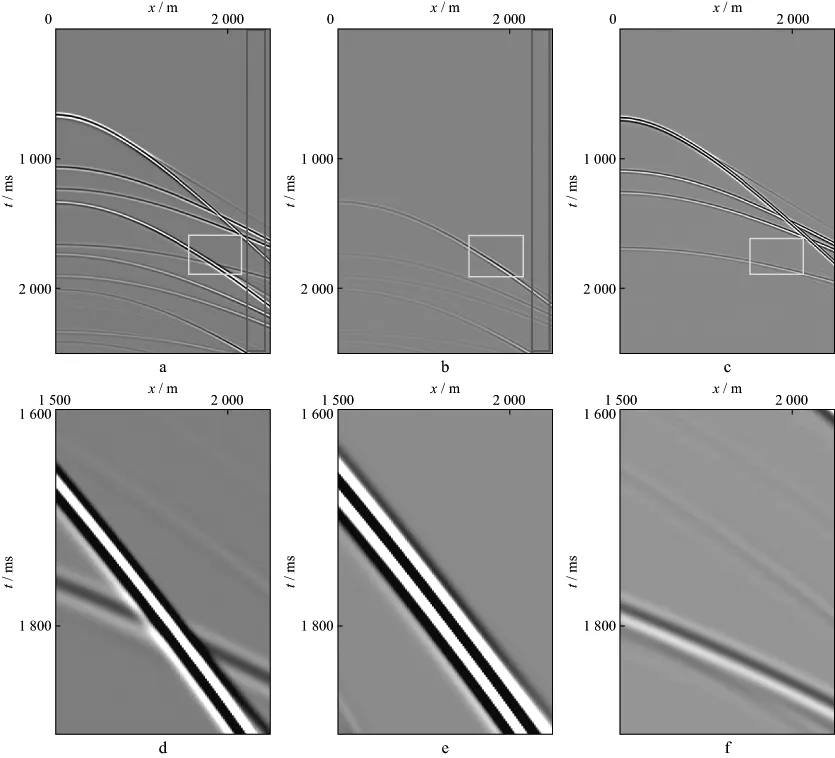
图5 合成单炮记录应用本文方法的多次波减去效果分析a 原始单炮记录; b 预测自由表面多次波模型; c 多次波减去结果; d 原始单炮记录中黄框所示区域的放大显示; e 预测自由表面多次波模型中黄框所示区域的放大显示; f 多次波减去结果中黄框所示区域的放大显示

3.3 实际地震资料应用试验

图7所示为我国某深海实际地震资料应用本文新减去方法的结果。其中,图7a为原始单炮记录,图7b为应用本文方法多次波减去后的记录,图7c 为反馈环模型预测的自由表面多次波。比较图7a和图7b可见,本文方法取得了较好的多次波减去效果,原始记录中大部分多次波已经被减去,

尤其是图中红框所示的一次波与多次波非正交的区域,减去结果中很好地保留了一次波。图8为实际地震资料共偏移距道集应用本文新减去方法的结果。比较图8a和图8b可见，多次波已被较好地压制。实际地震资料试验结果证明了本文方法的有效性。

图6 合成单炮记录中红框所示区域内数据的相似系数谱a 原始数据的相似系数谱; b预测多次波模型的相似系数谱; c Butterworth滤波后的相似系数谱; d Butterworth滤波相似系数谱经过平滑和阈值滤波后的结果

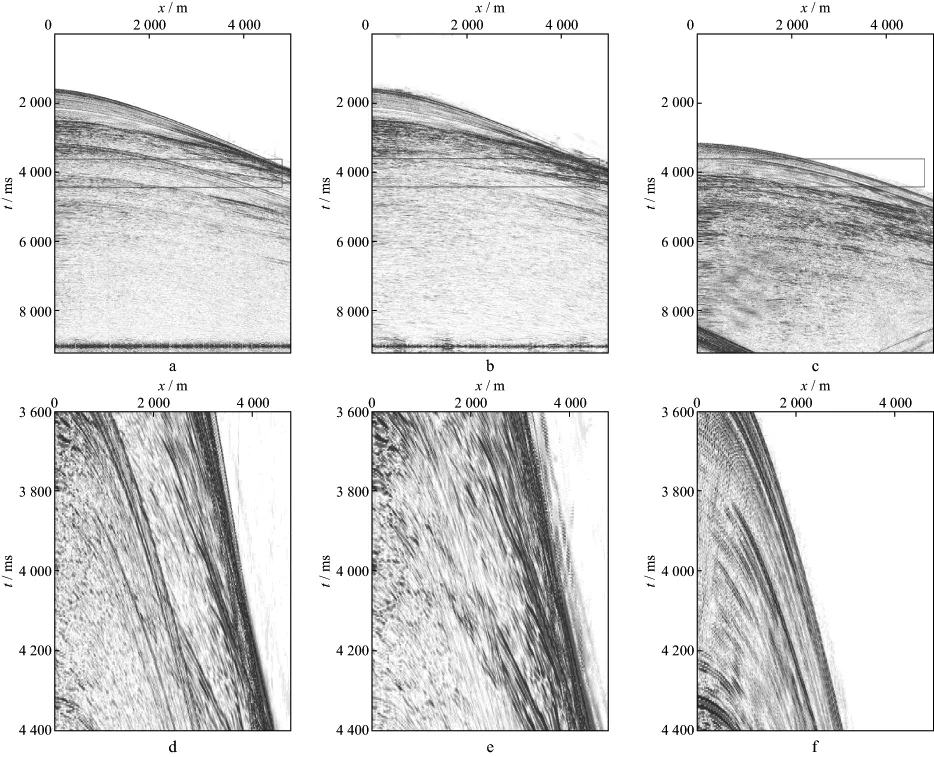
图7 实际地震资料单炮记录应用本文方法的多次波减去效果a 原始单炮记录; b 多次波减去结果; c预测多次波模型; d 原始单炮记录中红框所示区域放大显示; e 多次波减去结果中红框所示区域放大显示; f 预测多次波模型中红框所示区域放大显示

图8 实际地震资料共偏移距道集应用本文方法的多次波减去效果a 原始剖面; b 多次波减去结果; c 预测多次波模型

4 结束语

模拟数据测试和实际地震资料试验结果表明,本文提出的局部τ-p域基于相似系数谱约束的多次波自适应减去方法可以有效地实现多次波的自适应减去。该方法利用预测模型的相似系数谱来指示局部τ-p域原始数据中多次波存在的位置,根据相似系数谱的约束来设计滤波器,同时实现预测多次波模型与原始记录中多次波的振幅、相位和旅行时匹配,完成多次波的自适应减去。

与基于L2范数的多次波减去方法相比,相似系数谱的引入相当于对振幅进行归一化,从而不再需要通过求解线性方程组来实现振幅匹配,同时也提高了匹配过程的稳定性,突破了L2范数自适应减去准则的正交性和一次波能量最小的假设限制。此外,这种减去方法也可以减弱子波不一致性对减去过程的影响,在振幅匹配的同时,对相位和旅行时等属性也进行匹配,进一步改善了匹配效果。

参 考 文 献

[1] Berryhill J R,Kim Y C.Deep-water peg legs and multiples:emulation and suppression[J].Geophysics,1986,51(12):2177-2184

[2] Wiggins J W.Attenuation of complex water-bottom multiples by wave equation based prediction and subtracting[J].Geophysics,1988,53(12):1527-1539

[3] Berkhout A J,Verschuur D J.Estimation of multiple scattering by iterative inversion,part I:theoretical considerations[J].Geophysics,1997,62(5):1586-1595

[4] 金德刚,常旭,刘伊克.逆子波域消除多次波方法研究[J].地球物理学报,2008,51(1):250-259

Jin D G,Chang X,Liu Y K.Research of multiple elimination method in inverse wavelet domain[J].Chinese Journal of Geophysics(in Chineses),2008,51(1):250-259

[5] 黄新武,孙春岩,牛滨华.基于数据一致性预测与压制自由表面多次波—理论研究与试处理[J].地球物理学报,2005,48(1):173-180

Huang X W,Sun C Y,Niu B H.Surface-related multiple prediction and suppression based on data-consistence:a theoretical study and test[J].Chinese Journal of Geophysics(in Chineses),2005,48(1):173-180

[6] Weglein A B.Multiple attenuation:an overview of recent advances and the road ahead[J].The Leading Eage,1999,18(1):40-44

[7] Robinson E A.Predictive decomposition of seismic trace [J].Geophysics,1957,22(4):767-778

[8] Ryu J V.Decomposition(DECOM) approach applied to wave-field analysis with seismic reflection records[J].Geophysics,1982,47(6):869-883

[9] Hampson D.Inverse velocity stacking for multiple elimination[J].Expanded Abstracts of 56thAnnual Internat SEG Mtg,1986:422-424

[10] 胡天跃,王润秋,White R E.地震资料处理中的聚束滤波方法[J].地球物理学报,2000,43(1):105-115

Hu T Y,Wang R Q,White R E.Beamforming in seismic data processing[J].Chinese Journal of Geophysics(in Chinese),2000,43(1):105-115

[11] Weglein A B,Gasparotto P M,Stolt R H,et al.An inverse-scattering series method for attenuating multiples in seismic reflection data[J].Geophysics,1997,

62(6):1975-1989

[12] Guitton A.Adaptive subtraction of multiples using theL1-norm[J].Geophysical Prospecting,2004,52(1):27-38

[13] Monk D J.Wave-equation multiple suppression using constrained cross-equalization[J].Geophysics Prospecting,1993,41(6):725-736

[14] Wang Y H.Multiple subtraction using an expanded multichannel matching filter[J].Geophysics,2003,68(1):346-354

[15] 李鹏,刘伊克,常旭,等.均衡拟多道匹配滤波法在波动方程法压制多次波中的应用[J].地球物理学报,2007,50(6):1844-1853

Li P,Liu Y K,Chang X,et al.Application of the equipoise pseudomultichannel matching filter in multiple elimination using wave-equation method[J].Chinese Journnal of Geophysics(in Chineses),2007,50(6):1844-1853

[16] Spitz S.Pattern recognition,spatial predictability,and subtraction of multiple events[J].The Leading Eage,1999,18(1):55-58

[17] 陆文凯,骆毅,赵波,等.基于独立分量分析的多次波自适应相减技术[J].地球物理学报,2004,47(5):886-891

Lu W K,Luo Y,Zhao B,et al.Adaptive multiple wave subtraction using independent component analysis[J].Chinese Journal of Geophysics(in Chineses),2004,47(5):886-891

[18] Neidell N S,Taner M T.Semblance and other coherency measures for multichannel data[J].Geophysics,1971,36(3):483-497

[19] Buhl P.Direct mapping of seismic data to the domain of intercept time and ray parameter—a plane-wave decomposition[J].Geophysics,1981,46(3):255-267