含天然气水合物介质地震空白带成因研究

尤加春,冯 凯,王 成,杜漫霖,刘学伟

(1.中国地质大学(北京)地球物理与信息技术学院，北京100083;2.中国石油天然气股份有限公司海外勘探开发公司，北京100034)

天然气水合物是一种具有巨大潜在开发价值的新型海洋能源矿产,在世界各大海洋中均有广泛分布[1]。目前对于天然气水合物的勘探主要采用地震方法,地震剖面上水合物赋存区域出现的空白带(blanking zone)及似海底反射(BSR)等地球物理特征是识别海底天然气水合物的主要标志[2-3]。地震空白带和似海底反射作为天然气水合物地震识别的一个重要特征,同时也是目前天然气水合物地震识别方法研究的一个热点问题[4]。

地震空白带是存在于BSR之上的反射波振幅相较于正常的反射波振幅要弱的天然气水合物赋存区域[5]。对于地震空白带的存在与天然气水合物的关系有多种解说。Holbrook等[6]将布莱克海台阻抗差的减小,即振幅空白的原因归结为这一地区沉积的均质性。Shipley等[7]研究认为,振幅空白是沉积物孔隙充填天然气水合物造成的。但这两种观点都由于缺乏实际的地震模型而难以解释。孙春岩等[8]建立了水合物饱和度不随孔隙度变化(CGHC)以及水合物饱和度随孔隙度变化(VGHC)的模型,认为天然气水合物饱和度的变化是引起振幅空白的主要原因。但CGHC和VGHC模型建立在均匀介质假设之上,而实际情况是,天然气水合物在地层中大多是非均匀分布的,因此,上述模型还不足以解释地震空白带形成的原因。胡高伟等[9-10]利用弯曲元技术研究了含水合物松散沉积物的声学特征,认为天然气水合物在孔隙中生成时形成的悬浮粒子对超声波信号产生了散射衰减。这一现象为地震空白带形成原因的研究提供了一种新的思路。

认识地震空白带的成因有利于认识并探测天然气水合物在地层中的赋存状态。但对于天然气水合物地震空白带形成的原因,目前并未形成统一的认识。我们在前人工作的基础上,分析了渗透型天然气水合物(水合物在地层中非均匀分布)在地层中赋存的微观模型及南海神狐地区实际地震偏移剖面,尝试建立了一种天然气水合物非均匀分布的地球物理模型,利用该模型研究了水合物非均匀分布对地震反射波的散射影响及这种散射作用与水合物饱和度的关系,并据此给出了地震空白带形成的一种合理解释。

1 一阶应力-速度弹性波动方程及有限差分离散

正演计算的地震记录基于弹性波动方程。在均匀各向同性二维弹性介质下,x-z平面内的一阶应力-速度弹性波动方程[11-12]为

(1a)

(1b)

其中,τxx,τxz,τzz是应力张量;Ux,Uz分别为位移的水平分量和垂直分量;ρ为弹性介质的密度;λ,μ为拉梅系数。

在利用交错网格法求解一阶应力-速度弹性波动方程时,速度和应力是分别在t+Δt/2和t时刻进行计算的。在时间偏导上采用传统的二阶差分近似计算,在空间偏导上采用如下形式的高阶差分近似计算:

(2)

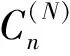
在利用有限差分、有限元等方法正演模拟地震波场传播规律时,激发的波场在模拟区域的边界会不可避免地产生边界反射,为此采用了吸收效果最佳的完全匹配层(PML)[13]边界条件。

2 含天然气水合物的非均匀双相孔隙介质模型

实际地层大多是多相孔隙介质,孔隙空间中填充的并不是单一的气相或液相物质,而是由液相、气相甚至其它固相介质(如冰、天然气水合物)组成的混合物质。鉴于此,我们以研究渗透型天然气水合物地震空白带的形成原因为背景,建立了水合物在地层中非均匀分布的双相孔隙介质模型,如图1所示。模型共4层,第1层为海水;第2(孔隙度为65%)和第3层(孔隙度为58%)为含天然气水合物储层;第4层为含气层,孔隙度为45%,孔隙空间中含气和水(气的饱和度为30%,水的饱和度为70%)。模型大小为2000m×2000m。模型中水合物呈非均匀随机分布,水合物非均匀分布的位置由随机函数给出[14-15],其中a,b分别为水平方向和垂直方向的自相关长度。根据南海神狐地区实际钻井资料,模型的岩石骨架由石英、黏土、白云母、斜长石和方解石按一定比例组成:第2层石英22%,白云母20%,斜长石8%,黏土30%,方解石20%;第3层石英37%,白云母20%,斜长石8%,黏土15%,方解石20%;第4层石英37%,白云母20%,斜长石8%,黏土15%,方解石20%。模型第2层和第3层中空白区为水饱和区,黑点区为含天然气水合物区。水饱和区不含天然气水合物,孔隙空间完全填充水,弹性参数可由Kuster-Toksoz等效介质理论(计算公式见附录A)和Gassmann方程计算得到。[16]图1中黑点区表示水合物赋存区,其微观模型为:岩石骨架(与水饱和区的岩石骨架完全相同)、天然气水合物及水。我们将天然气水合物作为固体骨架的一部分[17-18]来进行研究,以期得出定性上的一般认识和结论,并利用Helgerud等提出的等效介质理论计算水合物赋存区双相孔隙介质的弹性参数(参见附录B及文献[19])。

(3)

图1 含天然气水合物的岩石物理模型

3 数值模拟与分析

为研究孔隙度一定时、不同水合物饱和度情况下地震散射波的响应及其对地震空白带成因的影响,设计了天然气水合物饱和度分别为2%,10%,15%,20%,25%,30%,40%,50%,60%,70%和80%时的11种模型。图2是模型的纵波速度随天然气水合物饱和度变化的曲线,可见纵波速度随水合物饱和度的增大而增大。图3是天然气水合物饱和度为50%时的速度模型。

图2 纵波速度随天然气水合物饱和度变化的曲线

图3 天然气水合物饱和度为50%的模型纵波速度分布

有限差分正演计算的空间步长Δx=Δz=5m,时间步长Δt=0.001s。正演震源采用主频为45Hz的Ricker子波,震源深度200m。道间距为5m,炮间距为20m,一个排列设置有400个检波器,共正演计算100炮地震记录。

对正演计算得到的共炮集记录进行克希霍夫叠前深度偏移(偏移参数设置相同),图4是天然气水合物饱和度最大和最小时的偏移剖面。

对图4进行定性分析可见:在水合物饱和度较低时,模型中第2层与第3层的反射同相轴清晰可见,说明非均匀分布的水合物对地震反射波的散射衰减作用较弱。当水合物饱和度较大时,模型中第2层与第3层的反射同相轴几乎不可见,说明地层中非均匀分布的水合物对地震反射波的散射衰减作用较强。同时,海底与BSR之间的反射杂乱无章,反射同相轴发生错断,该现象与实际剖面的地震空白带颇为相似。说明在水合物饱和度达到一定数值时,实际海底中非均匀分布的天然气水合物可以造成地震波能量的较大衰减,使正常地层的反射同相轴消失,在地震剖面上出现空白带。

3.1 散射波、反射波相对能量变化分析

由不同天然气水合物饱和度的偏移剖面可见,随着地层中非均匀分布的水合物饱和度的变化,地震散射波、反射波的能量也相应发生了变化。为研究地震散射波、反射波的相对能量值随水合物饱和度的变化关系[20],也为进一步定量研究地层中非均匀分布的天然气水合物对地震波的散射衰减强度,在正演偏移剖面中划分了3个区域(对应模型中的位置见图1):①散射波zone-1区Ds,该区域用于研究含水合物区域的散射衰减;②层间反射波zone-2区Dr,该区域用于研究含水合物地层的层间反射衰减；③BSR反射zone-3区DBSR，该区域用于研究BSR处的反射衰减。在上述3个区域分别按照下列公式计算其能量Di:

图4 不同天然气水合物饱和度模型的正演偏移剖面a 水合物饱和度为2%; b 水合物饱和度为80%

(4)

其中，u(x,z)为偏移剖面中的波场值。散射波、反射波相对能量的定义分别为

(5)

图5为正演偏移剖面上散射波、反射波相对能量随天然气水合物饱和度变化的关系曲线。从图5 可见,在地层孔隙度一定时,模型中的层间反射波zone-2区域、BSR反射zone-3区域的相对能量变化趋势与水合物饱和度的变化趋势成反比,而散射波zone-1区域的相对能量变化趋势与水合物饱和度的变化趋势成正比。分析认为，出现这种现象的原因是:地层中非均匀分布的天然气水合物饱和度的增加,意味着孔隙流体中水合物微粒增多及孔隙流体饱和度减小。根据散射理论,水合物微粒增多增加了非均匀体对地震反射波的散射作用,使散射波相对能量增大,反射波相对能量减小。

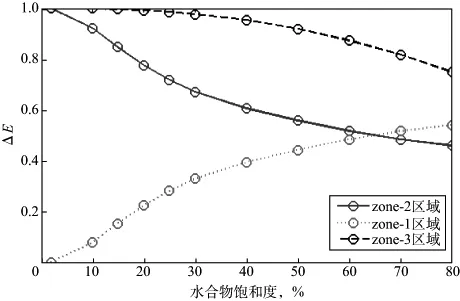
图5 正演偏移剖面上散射波、反射波相对能量随天然气水合物饱和度变化的关系曲线

进一步分析发现,当天然气水合物饱和度从2%增加到80%时,层间反射波zone-2区域的相对能量衰减率为54%。反射波振幅减弱正是地震空白带的主要特征,说明渗透型天然气水合物非均匀分布体对反射波的散射效应能使反射能量减弱而形成地震空白带,当水合物饱和度高到一定程度时,水合物不均匀体产生的散射波能量会增大到在地震空白带内产生“亮点”(图4b)。

从图5中同时发现:当地层中非均匀分布的天然气水合物的饱和度增加时,BSR反射zone-3区的相对能量衰减率为25%。与上述分析相同,在水合物饱和度达到一定数值时,地层中非均匀分布的天然气水合物对地震反射波的强烈衰减使BSR现象的可辨识度降低,这也可以用于解释为什么会在一些实际地震剖面中出现“存在天然气水合物而无BSR特征”的现象。

3.2 频率衰减梯度分析

地震空白带在动力学上表现为地震波高频能量的强烈衰减,这种能量衰减可以通过能量随频率的衰减梯度、指定能量比所对应的频率、指定频率段的能量比等物理参数来指示。本文讨论的频率衰减梯度[21]是衰减属性中的一种,它指示高频段的地震波能量随频率的变化情况,表征了能量衰减的程度。其计算公式为

(6)

其中,E1和f1表示总能量衰减到65%时的能量和频率,E2和f2表示总能量衰减到85%时的能量和频率。具体的计算方法为:首先对每道地震记录做时频分析,在时频剖面上把检测到的最大能量频率作为初始衰减频率,再计算65%和85%时的地震波能量分别对应的频率,在这个频率范围内,根据频率对应的能量值,拟合出频率与能量的衰减梯度,得到振幅衰减梯度因子,如图6所示。

为研究地震空白带的成因,计算了模拟地震记录的频率衰减梯度,绘制了图1所示模型中两个层间反射区域的频率衰减梯度值随天然气水合物饱和度的变化关系曲线(图7)。

图6 频率衰减梯度计算

从图7可见,在地层孔隙度一定、天然气水合物饱和度增加时,zone-2和zone-3区域的频率衰减梯度值也相应增大,说明地震能量衰减的程度增大,据此可以预见地震波能量应呈现减小趋势。这与图5中zone-2区域和zone-3区域的相对能量随水合物饱和度的增加呈减小趋势相吻合。出现这种现象的原因是当地层中非均匀分布的天然气水合物饱和度增加时,其对地震波的散射衰减作用增强,导致了地震波能量的衰减,进一步表现为频率衰减梯度的增加。

图7 zone-2区域(a)和zone-3区域(b)频率衰减梯度与天然气水合物饱和度的变化关系曲线

综合上述分析可见,对于渗透型天然气水合物,当其在地层中饱和度达到一定数值时,孔隙空间中非均匀分布的水合物微粒对反射波有较强的散射作用。结合正演偏移剖面(图4)、相对能量曲线(图5)、频率衰减梯度曲线(图7)对比发现:天然气水合物的非均匀分布对反射波振幅散射衰减较大,足以使水合物赋存区域反射波振幅相对于正常反射波振幅降低50%以上。在含高饱和度水合物的地层中,反射波振幅衰减更大,而反射波能量的衰减对应了偏移剖面上振幅的减弱。由此不难得出结论:当天然气水合物成藏模式为渗透型时,水合物在地层中的非均匀分布对反射波的散射衰减是地震振幅空白带形成的主要原因。

4 结束语

我们从弹性波动方程的一阶应力-速度方程出发,利用高阶交错网格有限差分正演方法计算了在地层孔隙度一定时、不同天然气水合物饱和度下地震散射波的响应,并对模拟结果进行了定性和定量分析,初步认为:地层中非均匀分布的天然气水合物产生的散射作用的强弱与水合物的饱和度成正比,是地震空白带形成的主要原因,并对BSR的形成也有重要影响。本文着重讨论的是渗透型天然气水合物在地层中非均匀分布对反射波的散射作用,对于天然气水合物成藏模式为扩散型时地震空白带的形成原因及不同的成藏模式对地震空白带形成的影响还有待进一步研究。

附录A Kuster-Toksoz等效介质理论

式中:Km,μm为背景介质m的体积模量和剪切模量;Ki,μi为第i种包含物的体积模量和剪切模量;xi为第i种包含物所占的体积百分比;Pmi,Qmi为在背景介质中加入包含物材料i后的效果(本文考虑包含物的形状为球形)。

附录B Helgerud等提出的等效介质理论计算公式

天然气水合物沉积层的体积模量Kdry与剪切模量Gdry的计算公式分别为

式中：φc为临界孔隙度(范围36%～40%);Ks为岩石骨架的体积模量;Gs为岩石骨架的剪切模量。

根据Hertz-Mindlin的理论,在岩石孔隙度为临界孔隙度时,干岩石骨架有效体积模量和剪切模量计算公式为

(B4)

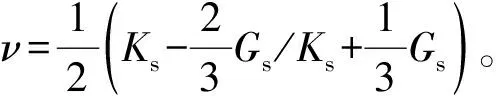
当水合物是骨架的一部分时,会使孔隙度减小,也会改变固体部分的体积模量、剪切模量和密度。固体部分的体积模量和剪切模量根据Hill平均方程修正为

(B5)

式中：m为组成岩石矿物成分的数目;fi为第i种矿物的体积百分比;Ki,Gi分别为第i种矿物的体积模量和剪切模量。

当孔隙空间中含有水和气体时,孔隙流体的体积模量利用等效介质理论进行计算,其公式为

(B6)

参 考 文 献

[1] Mikov A V,Sassen R.Preliminary assessment of resources and economic potential of individual gas hydrate accumulation in the Gulf of Mexico continental slope[J].Marine and Petroleum Geology,2003,20(2):111-128

[2] 宋海斌,松林修,杨胜雄,等.海洋天然气水合物的地球物理研究(Ⅱ):地震方法[J].地球物理学进展,2001,16(3):110-118

Song H B,Matsubayashi O,Yang S X,et al.Geophysical researches on marine gas hydrates(Ⅱ):seismic methods[J].Progress in Geophysics,2001,16(3):110-118

[3] 宋海斌,张岭,江为为,等.海洋天然气水合物的地球物理研究(Ⅲ):似海底反射[J].地球物理学进展,2003,18(2):182-187

Song H B,Zhang L,Jang W W,et al.Geophysical researches on marine gas hydrates(Ⅲ):bottom simulating reflections[J].Progress in Geophysics,2003,18(2):182-187

[4] Lee L M.Agena W F,Hutchinson D R.Amplitude blanking in seismic profiles from Lake Baikal[J].Marine and Petroleum Geology,1996,13(5):549-563

[5] 杨木壮,王明君,吕万军.南海西北陆坡天然气水合物成矿条件研究[M].北京:气象出版社,2008:35-47

Yang M Z,Wang M J,Lu W J.Geological factors for gas hydrates formation & distribution in the northwest continental slope of the south China sea[M].Beijing:China Meteorological Press,2008:35-47

[6] Holbrook W S,Hoskins H,Wood W T,et al.Methane gas-hydrate and free gas on the Blake Ridge from vertical seismic profiling [J].Science,1996,273(5283):1840-1843

[7] Shipley T H,Houston M H,Buffler R T,el at.Seismic evidence for widespread possible gas hydrate horizons on continental slopes and rises[J].AAPG Bulletin,1979,63(12):2204-2213

[8] 孙春岩,章明昱,牛滨华,等.天然气水合物地震空白带现象正演模型研究[J].地学前缘,2003,10(1):199-204

Sun C Y,Zhang M Y,Niu B H,et al.Modeling of seismic blanking zone for gas hydrate[J].Earth Science Frontiers,2003,10(1):199-204

[9] 胡高伟,业渝光,张剑,等.松散沉积物中天然气水合物生成、分解过程与声学特性的实验研究[J].现代地质,2008,3(3):465-474

Hu G W,Ye Y G,Zhang J,et al.Study on gas hydrate formation-dissociation and its acoustic response in unconsolidated sands[J].Geosciencs,2008,3(3):465-474

[10] 胡高伟,业渝光,张剑,等.基于弯曲元技术的含水合物松散沉积物声学特性研究[J].地球物理学报,2012,55(11):3762-3773

Hu G W,Ye Y G,Zhang J,et al.Acoustic properties of hydrate-bearing unconsolidated sediments based on bender element technique[J].Chinese Journal of Geophysics(in Chinese),2012,55(11):3762-3773

[11] 牛滨华,孙春岩.半空间均匀各向同性单相固体弹性介质与地震波传播-地震波传播理论与应用[M].北京:地质出版社,2005:63-67

Niu B H,Sun C Y.Half-space homogeneous isotropic single-phase solid elastic medium and seismic wave propagation[M].Beijing:Geological Press House,2005:63-67

[12] 董良国,马在田,曹景忠.一阶弹性波方程交错网格高阶差分解法[J].地球物理学报,2000,43(3):412-418

Dong L G,Ma Z T,Cao J Z.A staggered-grid high-order difference method of one-order elastic wave equation[J].Chinese Journal of Geophysics(in Chinese),2000,43(3):412-418

[13] Zeng Y Q,He J Q,Liu H Q.The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media[J].Geophysics,2001,66(4):1258-1266

[14] 奚先,姚姚.二维随机介质及波动方程正演模拟[J].石油地球物理勘探,2001,36(5):546-552

Xi X,Yao Y.2-D random media and wave equation forward modeling[J].Oil Geophysical Prospecting,2001,36(5):546-552

[15] 奚先,姚姚.二维弹性随机介质中的波场特征[J].石油地球物理勘探,2004,39(6):679-685

Xi X,Yao Y.Wavefield characters of 2-D elastic random medium[J].Oil Geophysical Prospecting,2004,39(6):679-685

[16] Mavko G,Mukerji T,Dvorkin J.The rock physics handbook:tools for seismic analysis in porous media[M].Cambridge:Cambridge University Press,2003:106-142

[17] 孙春岩,章明昱,牛滨华.天然气水合物微观模式及其速度参数估算方法研究[J].地学前缘,2003,10(1):191-198

Sun C Y,Zhang M Y,Niu B H.Micromodels of gas hydrate and their velocity estimation methods[J].Earth Science Frontiers,2003,10(1):191-198

[18] Ecker C.Seismic characterization of methane hydrate structure[D].Stanford:Stanford University,2001

[19] 宋海斌,松林修,吴能友,等.海洋天然气水合物的地球物理研究(Ⅰ):岩石物性[J].地球物理学进展,2001,16(2):118-126

Song H B,Matsubayashi O,Wu N Y,et al.Geophysical researches on marine gas hydrates(I):physical properties[J].Progress in Geophysics,2001,16(2):118-126

[20] 殷学鑫,刘洋.二维随机介质模型正演模拟及其波场分析[J].石油地球物理勘探,2011,46(6):862-871

Yin X X,Liu Y.Random medium 2D modeling and its wavefield analysis [J].Oil Geophysical Prospecting,2011,46(6):862-871

[21] Xiong X J,He X L,Pu Y,et al.High-precision frequency attenuation analysis and its application[J].Applied Geophysics,2011,8(4):337-343