一类线性Weingarten子流形的分类问题

杨 丹, 丁 宇, 黄坤龙

(沈阳大学 师范学院, 辽宁 沈阳 110044)

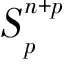
对于de Sitter空间中具有常数量曲率的完备的类空子流形Mn,Chaves等[5]证明了:如果Mn具有平行平均曲率向量且截面曲率是非负的,则Mn是全脐子流形或者是M1×…×Mk乘积流形,其中,Mi是全脐的.

线性Weingarten子流形是指平均曲率H和数量曲率R满足R=aH+b的子流形.线性Weingarten子流形是常数量曲率子流形的一种推广.本文主要考虑de Sitter空间中完备的类空线性Weingarten子流形.主要得到了如下结果.

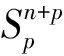
M1×M2×…×Mk.

式中,Mn是全脐子流形并且互相是正交的.

注1 如果Mn具有常平均曲率H和常数量曲率R,则必存在一个常数a,使得R=aH.因此,本文得到的定理是文献[5]中定理1.9 的一种推广.

1 预备知识

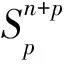
式中,εi=1(1≤i≤n),εα=-1(n+1≤α≤n+p).

本文做如下记号:

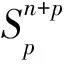
限制到Mn上,得到

ωα=0 (α=n+1,…,n+p).

诱导在Mn上的度量为

令

(1)

则二次型

⊗ωj⊗eα

是Mn的第二基本形式.令

Mn的平均曲率向量ξ定义为

平均曲率向量ξ的长度称为Mn的平均曲率,记为H.当ξ≠0时,选择平均曲率向量的方向为第一法向量的方向,使得

得到Mn的结构方程为

Gauss方程为

(2)

令Rij和R分别为Mn的Ricci曲率和标准化数量曲率,由式(2)知

此外,法曲率张量为

(5)

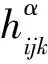
对式(1)微分,得到Codazzi方程:

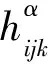
(7)

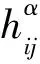
对式(7)求外微分,得到如下Ricci恒等式:

第二基本形式的拉普拉斯算子定义为

由式(7)和式(9)得到

由于

通过简单地计算得到

再由式(2)和式(5),通过直接计算知

式中,N(A)=tr(AA⊥).由于en+1与ξ的方向相同,得到ξ=Hen+1,且

Hn+1=H,Hα=0 (α=n+2,…,n+p).

(13)

由式(6)和式(13)知

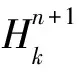
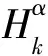
假设ξ/H是平行的,则ωn+1,α=0,且

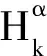
(14)

令

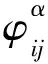
则由式(13)容易验证

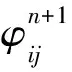
(17)

容易验证它是个无迹的张量,并且

(18)

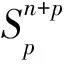
将式(13)～式(18)代入到 式(12)中得到

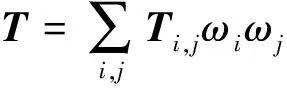
(20)

在式(20)中,令f=nH,由式(4)知

将式(19)代入到式(21),得到

引入如下算子:

为了完成定理的证明,还需要以下结果.

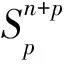
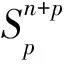
(n-1)a2+4n(1-b)>0,

则

此外,如果等式成立,则H是常数.

注2 当b<1时,由引理1知

此外,如果等式成立,则H是常数.

引理2[7]令B1和B2是对称的n×n阶矩阵,满足

[B1,B2]=O,trB1=trB2=0,

则

2 定理的证明

对于每一个法向量场eα,选择e1,…,en,使得

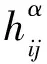
记截面曲率的下确界为KM, 则得到

所以

另外,容易验证

(25)

将式(14)、式(24)和式(25)代入到式(11)中得到

由式(21)和式(26)得到

由R=aH+b和式(27)知

由于Mn的截面曲率是非负的,由注2知

因为L是椭圆型算子,且平均曲率在Mn上能够达到最大值,所以H是常数,故

(1)LαLβ=LβLα(对所有的α和β),所以Mn的法丛是平坦的,所有的矩阵Lα能够同时对角化;

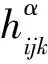
由式(1)、式(2)和式(23)可知

又由于Rijij≥0,从而

应用与文献[8]中引理 5.1、引理5.2、定理 1.3同样的方法可以得到如下结论:

Mn是全脐子流形或者是乘积流形M1×…×Mk,其中,Mi是全脐子流形并且互相是正交的.

参考文献:

[1]Cheng Qingming. Complete Space-like Submanifolds in a de Sitter Space with Parallel Mean Curvature Vector[J]. Mathematische Zeitschrift, 1991,206(1):333-339.

[2]Li Haizhong. Complete Spacelike Submanifolds in de Sitter Space with Parallel Mean Curvature Vector SatisfyingH2=4(n-1)/n2[J]. Annals of Global Analysis and Geometry, 1997,15(4):335-345.

[3]Shen Yibing, Dong Yuxing. On Complete Space-like Submanifolds with Parallel Mean Curvature Vector[J]. Chinese Annals of Mathematics,1998,19B(3):369-380.

[4]Brasil A, Chaves R M B, Colares A G. Rigidity Results for Submanifolds with Parallel Mean Curvature Vector in the de Sitter Space[J]. Glasgow Mathematical Journal, 2006,48(1):1-10.

[5]Chaves R M B, Sousa Jr L A M. Some Applications of a Simons’ Type Formula for Complete Spacelike Submanifolds in a Semi-Riemannian Space Form[J]. Differential Geometry and its Applications, 2007,25(4):419-432.

[6]Yang Dan, Hou Zhonghua. Linear Weingarten Spacelike Submanifolds in de Sitter Space[J].Journal of Geometry, 2012,103(1):177-190.

[7]Santos W. Submanifolds with Parallel Mean Curvature Vector in Spheres[J]. Tohoku Mathematical Journal, 1994,46(3):403-415.

[8]Ishihara T. Maximal Spacelike Submanifolds of a Pseudo-Riemannian Space of Constant Curvature[J]. The Michigan Mathematical Journal, 1988,35(3):345-352.