自旋为1/2的亚铁磁棱型X-Y链的内能
2014-03-25贾维烨葛崇员孙树生成泰民
贾维烨, 葛崇员, 孙树生, 成泰民
(沈阳化工大学 数理系, 辽宁 沈阳 110142)
低维磁性系统存在许多奇异的特性,因此这一领域的研究引起了科学家们广泛的兴趣[1-5].1997年Shiomi[1]等人通过实验合成出自旋为1/2交替的亚铁磁性复合物.2005年Kikuchi[2]等人通过实验发现Cu3(CO3)2(OH)2材料的磁化强度在低温下随外磁场的变化呈现1/3的磁化平台,在低温区磁化率随温度变化出现双峰等特性.2008年Rule[4]等人利用非弹性中子散射实验研究了蓝铜矿Cu3(CO3)2(OH)2材料的诸交换积分,并通过实验也发现了1/3的磁化平台的存在.2011年Jeschke[5]利用密度泛函理论从理论上研究了自旋为1/2的棱型链磁性质及诸交换积分,并利用第一性原理解释了这一阻挫材料的形成机理.
长程相互作用对系统热力学性质的影响近年来也被人们广泛关注[6-7],外场中具有长程相互作用自旋为1/2的亚铁磁棱型X-Y链的热力学性质也得到了相应研究.本文采用Jordan-Wigner(J-W)变换[8]分析方法对外场中Z方向具有均匀长程相互作用自旋为1/2的亚铁磁棱型X-Y链进行研究.利用不变本征算符(IEO)法[9-14]得到体系的元激发能谱,对体系的Hamiltonian进行对角化,并利用量子统计理论推导出体系配分函数和内能.
1 系统的Hamiltonian对角化及体系的内能
二聚体分子和单基体分子交替排列构成的自旋为1/2的亚铁磁棱型X-Y链如图1所示.其中S2,l和S3,l表示二聚体分子的量子自由基,S1,l表示单基体分子的量子自由基.JF=-ηJ(η,J>0)表示二聚体分子内的铁磁相互作用,JAF=μJ(μ,J>0)表示二聚体分子与单基体分子间的反铁磁相互作用,并且假设这样的循环结构具有N个(l=1,2,…,N).
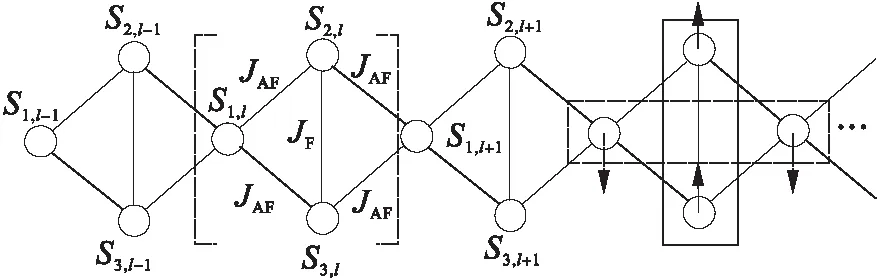
图1 自旋为1/2的亚铁磁棱型X-Y链系统
上述相互作用利用Heisenberg相互作用理论模型描述,那么系统的Hamiltonian可用如下形式表示:
(1)
式(1)中:Si,l是自旋1/2的量子算符,S2,l和S3,l由二聚体分子内的铁磁相互作用JF<0耦合连接,其他作用都由二聚体分子与单基体分子间的反铁磁相互作用JAF>0耦合连接,uB为玻尔磁子,g为朗德因子,H表示外磁场强度.
对式(1)的自旋升降算符进行Jordan-Wigner(J-W)变换[8,11-14]:
(2)
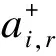
(3)
(4)
其中:
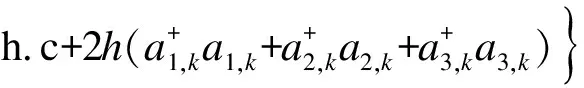
(5)
其中:h=guBH,h.c.表示前项的厄米共轭,并且γk=exp(ik).
令系统哈密顿量的IEO算符为:
τ3,σa3,k, (σ=1,2,3)
(6)
由式(6)可得:
(7)
根据式(6)及利用IEO法可得自旋为1/2的亚铁磁棱型X-Y链系统的元激发能量:
(8)
将式(6)和(7)代入式(5)可得:
(9)
根据式(4)和(9),利用量子统计理论可得系统的配分函数:
(10)
其中β=1(kBT) .
由式(10)可得系统的内能:
(11)
2 讨 论
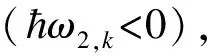
HC1=ηJ/(2guB)
(12)
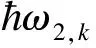
(13)
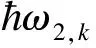
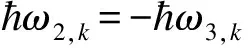
Hpeak=ηJ/(4guB)
(14)
当Hpeak≤H≤HC2时,Hpeak是外磁场下体系的磁化强度随温度的变化曲线出现峰值的临界磁场强度.
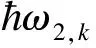
根据式(8)、(11)通过数值计算可得图2~图5结果.
由图2、图3可知,体系的内能随外加磁场的增加逐渐减少.由图2可知:当体系处于绝对零度(kBT/JAF=0)时,二聚体分子的铁磁相互作用JF与单基体与二聚体分子之间的反铁磁相互作用JAF之比(-JF/JAF)越大,在低外磁场区体系的内能越小.但是在高外磁场区(即guBH/JAF>2.5)该比值(-JF/JAF)对体系的内能几乎无影响,在此表现为对于不同的JF/JAF体系内能随外磁场变化曲线,在高外磁场区重分为一条曲线.由图3可知:在有限温度下(kBT/JAF=0.5),在低外磁场区(-JF/JAF)越大,也出现体系内能减少的现象.但是与绝对零度不同的是,对于不同的-JF/JAF,体系内能在有限温度下随外磁场的变化曲线在更高的外磁场下(即guBH/JAF=3.3)出现重合,且在大外磁场下(即guBH/JAF>4.0)时,曲线重合出现分裂的迹象.这说明在此存在如下4种形式的能量之间的竞争:与温度相关的热无序能(kBT/JAF)、与外磁场强度相关的自旋磁矩势能(guBH/JAF);使二聚体分子内电子自旋平行排列的铁磁交换作用能(JF);使二聚体与单基体分子间电子自旋反平行排列的反铁磁交换作用能(JAF).
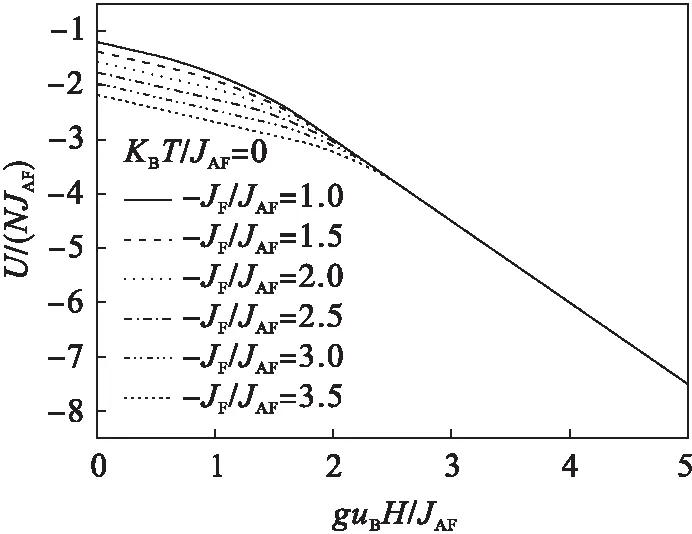
图2 在绝对零度下(kBT/JAF=0)对于不同 JF/JAF体系内能随外磁场的变化
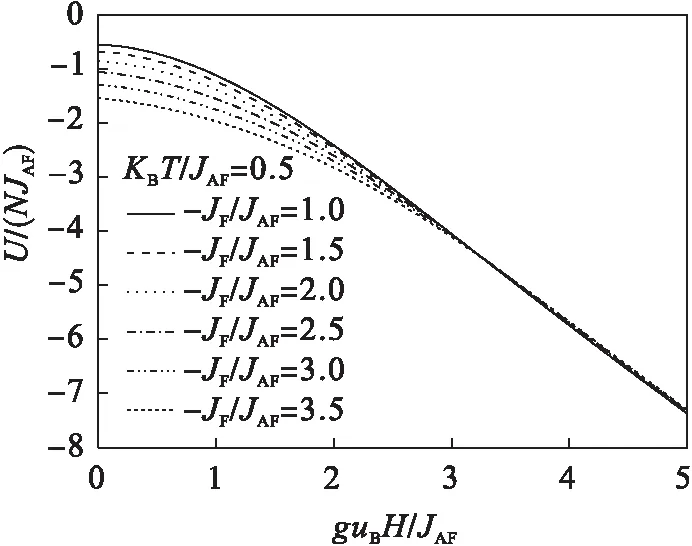
图3 在有限温度下(kBT/JAF=0.5)对于不同 JF/JAF体系内能随外磁场的变化
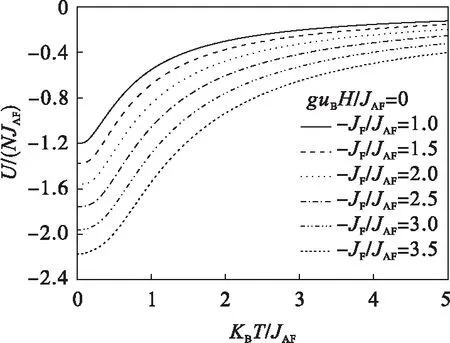
图4 在无外磁场下(guBH/JAF=0)对于不同的 JF/JAF体系内能随温度的变化
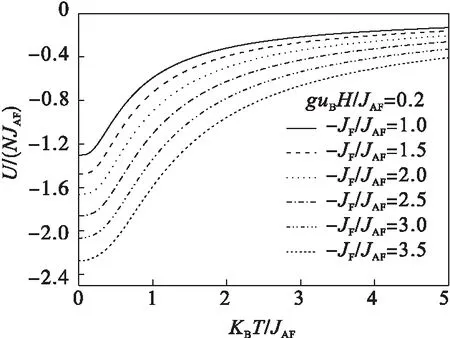
图5 在有限外磁场下(guBH/JAF=0.2)对于不同的 JF/JAF体系内能随温度的变化
由图4、图5可知:体系的内能随温度的升高逐渐增大,并且在低温区出现U~T曲线向上弯曲和在高温区出现向下弯曲的现象.这说明在低温区,自旋为1/2的亚铁磁棱型X-Y链体系容易出现比热异常的峰,从而将出现比热双峰现象.但是,比较图4和图5可知在有限外加磁场下,体系的内能比无外加磁场时更小.
3 结 论
在有限温度与有限外磁场下,对于自旋为1/2的亚铁磁棱型X-Y链体系内能的研究得出如下主要结果:
(2) 外磁场强度H
(3) 体系的内能随外加磁场的增加逐渐减少;体系的内能随温度的升高逐渐增大.
(4) 绝对零度下,在高外磁场区二聚体分子内电子自旋平行排列的铁磁交换作用能JF与二聚体与单基体分子间电子自旋反平行排列的反铁磁交换作用能JAF之比(-JF/JAF)对体系的内能几乎无影响.但在有限温度、大外磁场下时,曲线重合出现分裂迹象.说明在该体系存在不同形式能量之间的竞争.
参考文献:
[1] Shiomi D,Nishizawa M,Sato K,et al.A Prerequisite for Purely Organic Molecule-based Ferrimagnetics:Breakdown of Simple Classical Pictures[J].J.Phys.Chem.B,1997,101(17):3342-3348.
[2] Kikuchi H,Fujii Y,Chiba M,et al.Experimental Observation of the 1/3 Magnetization Plateau in the Diamond-chain Compound Cu3(CO3)2(OH)2[J].Phys.Rev.Lett.,2005,94(22):227201.
[3] Maekawa K,Shiomi D,Ise T,et al.Theoretical Study on Spin Alignments in Ferromagnetic Heterospin Chains with Competing Exchange Interactions:A Generalized Ferrimagnetic System Containing Organic Biradicals in the Singlet Ground State[J].J.Phys.Chem.B,2005,109(19):9299-9304.
[4] Rule K C,Wolter A U B,Sullow S,et al.Nature of the Spin Dynamics and 1/3 Magnetization Plateau in Azurite[J].Phys.Rev.Lett,2008,100(11):117202.
[5] Jeschke H,Opahle I,Kandpal H,et al.Multistep Approach to Microscopic Models for Frustrated Quantum Magnets:The Case of the Natural Mineral Azurite[J].Phys.Rev.Lett,2011,106(21):217201.
[6] Haldane F D M.Nonlinear Field Theory of Large Spin Heisenberg Antiferromagnets:Semiclassically Quantized Solitons of the One-dimensional Easy-axis Néel State[J].Phys.Rev.Lett.,1983,50(15):1153-1156.
[7] Maisinger K,Schollwock U,Brehmer S,et al.Thermodynamics of the (1,1/2) Ferrimagnet in Finite Magnetic Fields[J].Phys.Rev.B,1998,58(10):R5908-R5911.
[8] Batista C D,Ortiz G.Generalized Jordan-Wigner Tr-ansformations[J].Phys.Rev.Lett,2001,86(6):1082-1085.
[9] Fan H Y,Li C.Invariant ‘Eigen-operator′ of the Square of Schrödinger Operator for Deriving Energy-level Gap[J].Phys.Lett.A,2004,321(2):75-78.
[10] Fan H Y,Wu H.Deriving Vibrating Modes of Some Multiatom Molecules by Virtue of the Invariant Eigenoperator Method[J].Modern Physics Letters B,2005,19(26):1361-1366.
[11] 成泰民,孙树生,贾维烨,等.自旋为1/2的X-Y模型亚铁磁棱型链的热力学性质[J].低温物理学报,2012,34(6):417-424.
[12] 成泰民,葛崇员,孙树生,等.自旋为1/2的XY模型亚铁磁棱型链的物性和有序-无序竞争[J].物理学报,2012,61(18):187502.
[13] 成泰民,王蕴鹏.低温下自旋为1/2的X-Y亚铁磁棱型链的元激发谱[J].沈阳化工大学学报,2012,26(3):270-273.
[14] 成泰民,王蕴鹏,葛崇员,等.低温下自旋为1/2的一维亚铁磁棱型链系统的元激发谱[J].大学物理,2012,31(1):5-8.
[15] Jacobs I S.Spin-flopping in MnF2by High Magnetic Fields[J].J.Appl.Phys.,1961,32:S61-S62.
[16] Karadamoglou J,Papanicolaou N.Bulk and Surface Spin-flop Transitions in an Antiferromagnetic XYZ Chain[J].Phys.Rev.B,1999,60(13):9477.
[17] Sakai Toru.Spin Flop in One-dimensional Quantum Antiferromagnets[J].Phys.Rev.B,1999,60(9):6238.
