LMBP神经网络算法的改进

高淑芝， 徐晓剑, 王 会， 赵 娜

(1.沈阳化工大学 信息工程学院， 辽宁 沈阳 110142； 2.葫芦岛锦化化工集团有限责任公司， 辽宁 葫芦岛 125000)

近年来针对如何提高LMBP算法的收敛速度和精度以及防止陷入局部极小值等特点，很多专家学者提出了自己的看法和主张，如模拟退火法[1]，趋药分类法[2]，Alopex算法[3]，Wilamowski改进了原有的LMBP算法，减少了矩阵求逆的计算量[4]，Xu提出平方根法分解系数矩阵，提高了LMBP算法的收敛速度[5]，Li等提出共轭梯度法与LMBP算法结合，避免了矩阵求逆的计算量[6].Chen等人指出其中的算法参数保持不变从而导致误差平方和摆动影响收敛速度[7].Shi等人针对步长因子限制比例系数进行分析，提出变步长新规则[8].

本文提出将逆矩阵G-1移到等式左边用直接分解法LU求解方程，避免了矩阵的求逆过程，并且将步长设置为一个可以调整的变量.

1 LMBP算法的改进

1.1 标准LMBP算法

设误差目标函数为:

(1)

其中:

eij=tij-yij

(2)

为网络误差向量，vi(x)为误差向量.由牛顿法:

xk+1=xk-(▽2f(xk))-1▽f(xk)

(3)

则:

Δx=-[▽F2(x)]-1▽F(x)

(4)

(5)

可以证明:

▽F(x)=JT(x)e(x)

(6)

当解靠近极值点时:

S(x)=0

(7)

则

Δ(x)=-[JT(x)J(x)]-1JT(x)e(x)

(8)

将(8)式进行改进，使其既包含高斯-牛顿法又具有梯度下降法的混合形式.公式为：

Δ(x)=-[JT(x)J(x)+IU]-1·

JT(x)e(x)

(9)

式中:I为单位矩阵，U为比例系数，若U接近于0时，则为高斯-牛顿法，若U值较大时，近似于梯度下降法Δx≈-▽F(x)/2U，通常的调整策略是算法开始时U取一小的正值，如果某一步不能减少误差目函数F(x)的值，则U乘以一个大于1的步进因子θ，即U=Uθ，如果某一步产生了更小的F(x)，则U在下一步除以θ，即U=U/θ.

1.2 LMBP算法的改进

对LMBP算法进行深入研究，发现其中涉及的矩阵[JTJ+IU]-1是影响其收敛的主要因素，通过使用LU直接分解法去除耗时的矩阵求逆运算，极大地减少了LMBP的计算量.可令：

A=[JTJ+IU]-1

(10)

-Δx=x

(11)

JTe=b

(12)

则公式(9)可以改为:

Ax=b

(13)

可以利用LU直接分解法对A进行对称三角分解.求Ax=b的问题就等价于求出:

A=LU

(14)

再根据：

Ly=b

(15)

又有：

Ux=y

(16)

可求出x.

使用LU分解法求解Δx不需要求逆矩阵，此时只需n3/3次乘除运算，运算速度可提高3倍以上.由于运算次数的减少，不但Δx以节省运算时间，还能减少舍入误差，因此，这种改进使算出的值更精确.

在实际计算中，随着U的增大，会发生小步长的问题，导致一次迭代在小步的循环中需循环多次，用很长的时间才能结束.为解决这一问题，将原来固定的θ值设计为变步长方式，即步长因子θ是一个可变的量.变步长公式定义为：

θ′=2k-αθ

(17)

式中：k为只有进入此步小循环的次数，a∈[0,1]为调整变量[9].

如果某一步不能减少误差目函数F(x)的值，则U乘以一个新的步进因子θ′，U=Uθ′，如果某一步产生了更小的F(x)，则U在下一步除以新的步进因子θ′，即U=U/θ′.

2 仿真研究

仿真的数据是方大锦化化工科技股份有限公司的历史数据，2011年11月用DCS变频器从现场采集，用1周时间采集500组数据，然后用基于改进差别矩阵属性约简的方法选取50组数据作为训练样本，用决策表选取S1、S2、S3、S4、S5、S6、S7、S8作为条件属性[10]，对应故障征兆，即：聚合反应温度(℃)、聚合反应压力(MPa)、搅拌电流(A)、注水流量轴封(m3/h)、夹套流量(m3/h)、冷却水温度(℃)、冷却水水压(MPa)、出口挡板温度(℃).聚合釜的历史数据及训练测试数据如表1所示.

表1 聚合釜运行历史数据

首先对所有数据作归一化处理，使数据在[0,1]之间.

归一化的处理公式：

(18)

为比较LMBP改进算法的性能，本文仿真针对传统BP算法，标准LMBP算法，改进LMBP算法.

(1) 传统BP算法：对应的函数是Traingd，训练次数net.epochs=1 000，训练目标net.goal=0.01，学习速率LP.lr=0.1.仿真结果如图1所示.

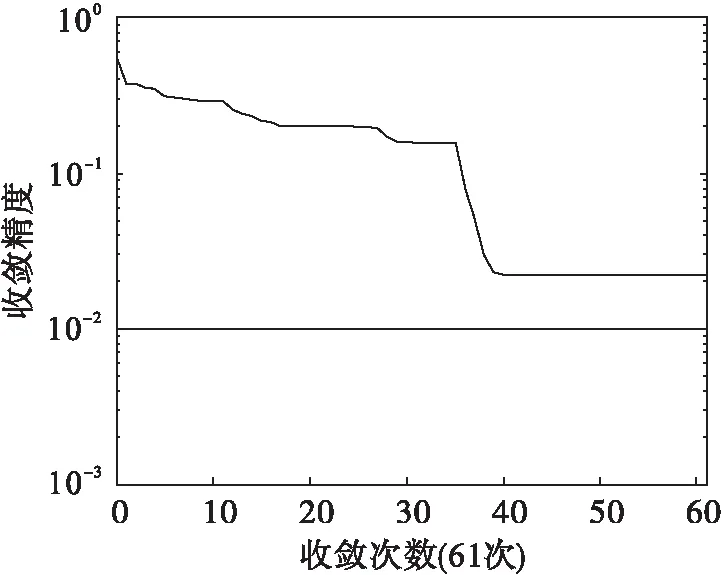
图1 传统BP算法的收敛次数

(2) 标准LMBP算法：对应函数Trainlm，训练目标net.goal=0.01，学习速率LP.lr=0.1.仿真结果如图2所示.

图2 标准LMBP算法的收敛次数

(3) 改进LMBP算法：调用自己编制的Mytrainlm子程序.仿真结果如图3所示.

图3 改进LMBP算法的收敛次数

由表2可总结出:传统BP算法的收敛次数61还没收敛，精度是0.022 222 2，标准LMBP算法的迭代是29次，精度0.002 444 27，是比较理想的结果，而改进LMBP算法的收敛次数是17，精度达到0.001 609 93，在聚合釜故障诊断中训练速度最快、精度最高.

表2 改进LMBP算法到达指定误差所需的 迭代次数和训练误差

3 总 结

提出了一种基于改进LMBP神经网络算法，对LMBP算法的权值与偏置值增量进行改进，首先，将逆矩阵G-1移到等式左边，用LU直接分解法求解方程，使计算量大为减少.然后用变步长代替固定步进因子，减少了循环次数.仿真实验结果表明采用此算法在聚合釜故障诊断中训练速度快、精度高.

参考文献：

[1] Jiao Licheng.Computation in Neural Networks[M].Xi’ an:Xidian University Press,1993:70-76.

[2] Hu Shouren.Technological Realzation and Application of Neutral Network[D].Changsha:Changsha National University of Defense Technology,1993:121-128.

[3] Venugopal K P.Pandya A S.Alopex Algorithm for Trining Mutilayers Neural Networks[C].China:IEEE Int Jconf on NN,1991：2-3.

[4] Wilamowski B M,Iplikci S,Kaynak O,et al.An Algorithm for Fast Convergence in Tranining[J].Neural Networks,2001,3:1778-1782.

[5] Xu Wenshang,Yu Qingming,Sun Yanliang,et al.Research on Methods of Improving the Training Speed of LMBP Algorithm and Its Simulation in Application[G].USA:IEEEE Computer Society Washington,DC,2007:540-545.

[6] Li Yeli,Feng Chao,Lu Lijun.Impoved Learing Algorithm for LMBP Based on Conjugate Gradient Methods[J].Computer Engineering and Application,2008,44(21):106-108.

[7] Chen T C,Han D J,Au F T K,et al.Acceleration of Levenberg Marquardt Training of Nenral Networks with Variable Decay Rate[J].Neural Networks,2003(3):1873-1878.

[8] Shi Buhai,Zhu Xuefeng.On Improved Algorithm of LMBP Neural Networks[J].Control Engineering of China,2008,15(2):164-167.

[9] 史步海，朱学峰.LMBP神经网络改进算法的研究[J].控制工程，2008,15(2):165-167.

[10] 高淑芝，王介生，高宪文.基于改进差别矩阵属性约简的聚合釜粗糙集-神经网络故障诊断[J].化工学报，2011,3(3)：62-63.