基于KPCA频谱特征提取的球磨机负荷建模方法

冯 雪， 赵立杰， 郑瀚洋

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

球磨机在选矿、陶瓷、化工、水泥、玻璃、耐火材料等行业中已经成为一种不可缺少的机器设备，它是物料被破碎之后，再进行粉碎的关键设备，也是工业生产中广泛使用的高细磨机械之一[1].球磨机通过筒体的旋转产生离心力，带动筒内钢球做抛物运动对物料进行撞击，从而达到将物料粉碎的目的.在球磨机运行过程中，对球磨机运行状态密切相关参数(如料球比、填充率和磨矿浓度)的预报能够有效降低球磨机的耗能，并提高产品质量.但是球磨机内部运行环境十分恶劣，在筒体内部安装传感器进行状态检测的方法存在着传感器易损坏，维修不方便等问题.近年来，基于球磨机外部响应振动信号进行球磨机内部状态参数预报的方法越来越受到关注[2].球磨机的外部振动信号含有大量与内部运行状态密切相关的信息.但时域振动信号中含有大量的噪声，因此在进行特征识别过程中存在很大困难.在对振动信号频谱分析过程中发现，尽管振动信号的频谱更能体现信号特征，但球磨机振动频谱却存在超高维和共线性的问题.为建立更有效的磨机负荷模型，在此领域进行了大量的研究.汤健等[3]提出了通过递归主元分析(RPCA)和最小二乘支持向量回归机(LSSVR)集成的方式，建立了磨机负荷软测量模型；采用基于主元分析特征提取和径向基函数(RBF)变换建立回归模型[4].

极限学习机(extreme learning machine，ELM)[5]是一种简单易用、有效的学习算法.它是一种单隐层前馈神经网络SLFNs学习算法，与传统的梯度学习算法(如BP算法)和SVM相比，ELM的学习速度更快，可以克服传统梯度算法常有的局部极小、过拟合和学习率选择不合适等问题，并且有更好的泛化能力[6].极限学习机只需要设置网络的隐层节点个数，在算法执行过程中不需要调整网络的输入权值以及隐元的偏置，并且产生唯一的最优解.ELM已被广泛应用于各类测量模型的建立及故障诊断之中，基于ELM可以建立具有良好泛化能力的温度软测量模型[6]；肖冬等[7]采用改进型ELM方法，将PCA与ELM相结合，建立了穿孔机导盘转速测量模型.

尽管ELM算法能够建立有效的预报模型，但是球磨机振动频谱存在超高维和共线性问题，频谱中不相关的频谱成分将会恶化模型质量，降低模型的准确性.为了提高球磨机负荷参数预报模型的准确性，本文采用核主成分分析KPCA(Kernel Principal Component Analysis)[8]方法对筒体振动频谱进行分析，KPCA是一种非常有效的数据压缩技术，它能够提取数据中互不相关的主元成分，有效地降低数据维数[9]，找到与球磨机运行状态相关的频谱特征.KPCA通过核函数引入非线性变换，首先将输入映射到特征空间，再做主元分析PCA[10]，得到振动频谱的主元，然后再采用极限学习机ELM算法对振动特征频谱建模，得到有效的球磨机负荷参数预报模型.

1 基于KPCA频谱特征提取的ELM建模方法

1.1 KPCA基本原理

KPCA方法的基本思想是通过某种隐式方式将输入空间映射到某个高维空间(常称为特征空间)，并且在特征空间中实现PCA.

假设x1,x2,…,xM为训练样本，用{xi}表示输入空间，相应的映射为Φ，在对{xi}进行标准化处理后，对其进行映射为Φ的非线性变换，所得特征空间中的协方差矩阵C为：

(1)

其中M为训练样本个数.

求解KPCA的变换可以通过求C的特征值和特征向量来完成.

Cv=λv

(2)

其中v为特征值λ的特征矢量.考虑到所有的特征向量可表示为Φ(x1),Φ(x2),…,Φ(xM)的线性张成，即

(3)

其中αi为第i个训练样本对应的特征向量.

考虑等式：

Φ(xi)·Cv=λ(Φ(xi)·v)

(4)

将(1)、(3)带入等式(4)，并令Kij=Φ(xi)·Φ(xj);i,j=1,2,…,M.得到

Mλα=Kα

(5)

其中：Mλ为K的特征值，α=[α1,α2,…,αM]为对应的特征向量.求解式(2)，便得到测试样本在特征空间的第h个特征矢量vh方向上投影的主成分gh(x).

gh(x)=vh·Φ(x)=

(6)

由于特征空间的维数很高，计算点积非常困难，因此采用核函数K(xi,x)=Φ(xi)·Φ(x)进行替换得到.

(7)

1.2 极限学习机ELM算法

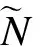
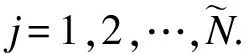
(8)

式(8)可以简写为

Hβ=Y

(9)

其中:

(10)

(11)

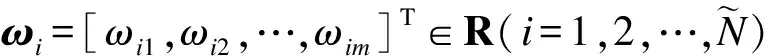
(12)

其中H*表示隐含层输出矩阵H的Moore-Penrose广义逆.

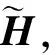
(1) 随机产生输入权值ωi和阀值bi；

(2) 计算隐含层输出矩阵H；

1.3 基于KPCA频谱特征提取的球磨机ELM建模

球磨机振动特征提取建模策略如图1所示.首先对球磨机外部振动信号进行数据采集，数据采集过程在XMQL 420×450格子型球磨机数据采集系统上进行.然后将采集到的振动信号进行时频变换，得到其对应频谱.对频谱做KPCA核主元分析处理，得到振动频谱的主元.最后以振动频谱主元作为输入，磨机负荷参数磨矿浓度、填充率和料球比作为输出，进行ELM极限学习机算法学习.

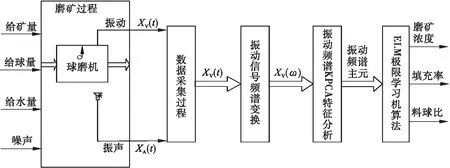
图1 基于KPCA频谱特征提取的球磨机ELM建模策略Fig.1 Strategy map of building ELM model based on KPCA

球磨机振动信号分析建模过程如下：

(1) 首先采集球磨机筒体振动信号，数据预处理后去除离群点和噪声.筒体振动信号时域波形经PWELCH方法变换为频域功率谱[11]，多个旋转周期频谱均值作为功率谱.

(2) 设球磨机筒体振动频谱数据为X∈RN，N为频谱长度，采用非线性变换Φ(X)将振动频谱映射到高维特征空间S上.

(3) 在频谱特征空间S上进行PCA主成分分析.一般选取的主元个数h的累积方法贡献率Sh大于85 %，即Sh=arg min={Sh≥85 %}.

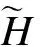
(5) 以ELM模型对比分析的均方根误差RMSE和决定系数(R2)作为最佳隐含节点数的评价标准，选择均方根误差越小，且决定系数越大的为最佳隐含节点数.RMSE和R2定义如下：

(11)

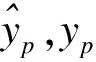
(6) 将ELM输入参数设置为最佳隐含节点数，根据主元个数h累积方差贡献率Sh大于85 %得到基于KPCA特征提取的ELM磨机负荷操作参数估计的较佳的测量结果.

2 球磨机负荷参数预报实验结果

2.1 磨矿浓度参数预报结果

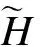
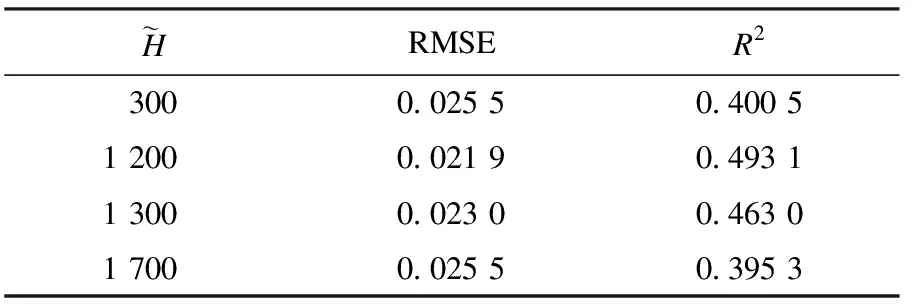
表1 隐含层节点数不同时磨矿浓度测试结果Table 1 The result of grinding density with different node number

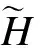
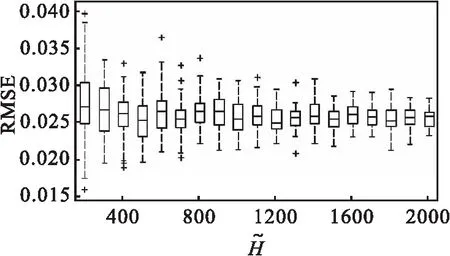
图2 磨矿浓度均方根误差分布箱线图Fig.2 Box plots of grinding density RMSE

基于振动频谱进行磨矿浓度参数预报，将基于KPCA建立的ELM模型与点数为1 200的ELM模型，振动频谱PLS模型和基于PCA，PLS振动频谱特征提取的ELM模型进行对比.以真实值与预测值的RMSE 作为模型性能的评价标准，同时引入相对均方根误差(RRMSE)作为评价标准，以克服RMSE受量纲变化的影响.RRMSE 定义如下：

(12)

RMSE和RRMSE越小，模型性能越好，预报越准确.各模型误差如表2所示.由表2可知：基于KPCA特征提取建立的ELM模型拥有最小的RMSE.尽管RRMSE要稍大于PCA结果，但是仍然远远小于其他方法，这说明相较于其他方法KPCA_ELM模型拥有较高的准确性.

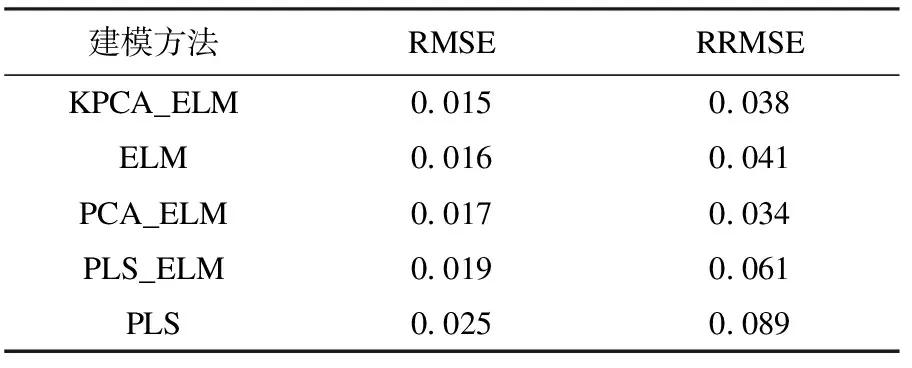
表2 不同方法磨矿浓度预报结果误差Table 2 RMSE and RRMSE of grinding density with different method

采用不同建模方法对磨矿浓度预报的结果如图3所示.图3中将KPCA_ELM模型，直接ELM模型，PCA_ELM模型，PLS_ELM模型和PLS模型的预报结果与真实值进行对比.结果显示：各模型的预报值与真实值均相差较小，因此拥有更小误差的基于KPCA特征提取的ELM模型性能更优越.

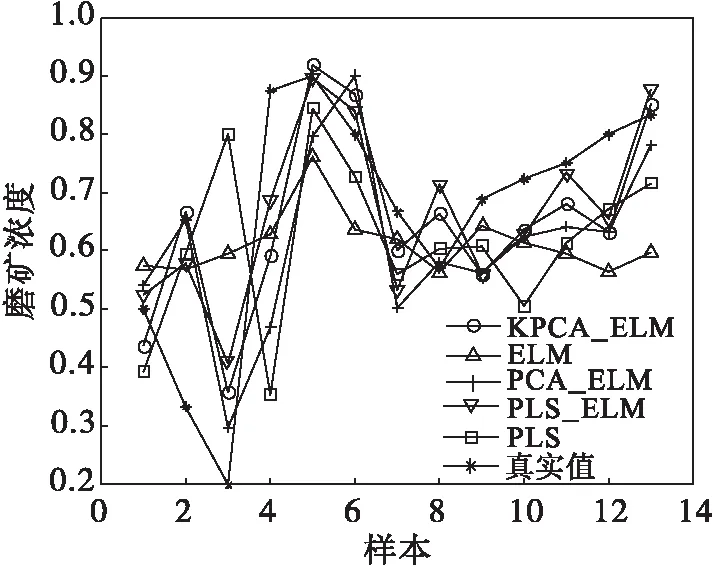
图3 磨矿浓度预报结果Fig.3 The prediction results of grinding density

2.2 填充率、料球比参数预报结果

对球磨机状态参数填充率和料球比进行参数预报，根据均方根误差，决定系数及均方根误差的分布情况选择最佳隐含节点数.不同节点数的填充率、料球比均方根误差分布情况如图4所示.确定填充率和料球比的ELM模型的隐含层节点数分别为1 200和900.

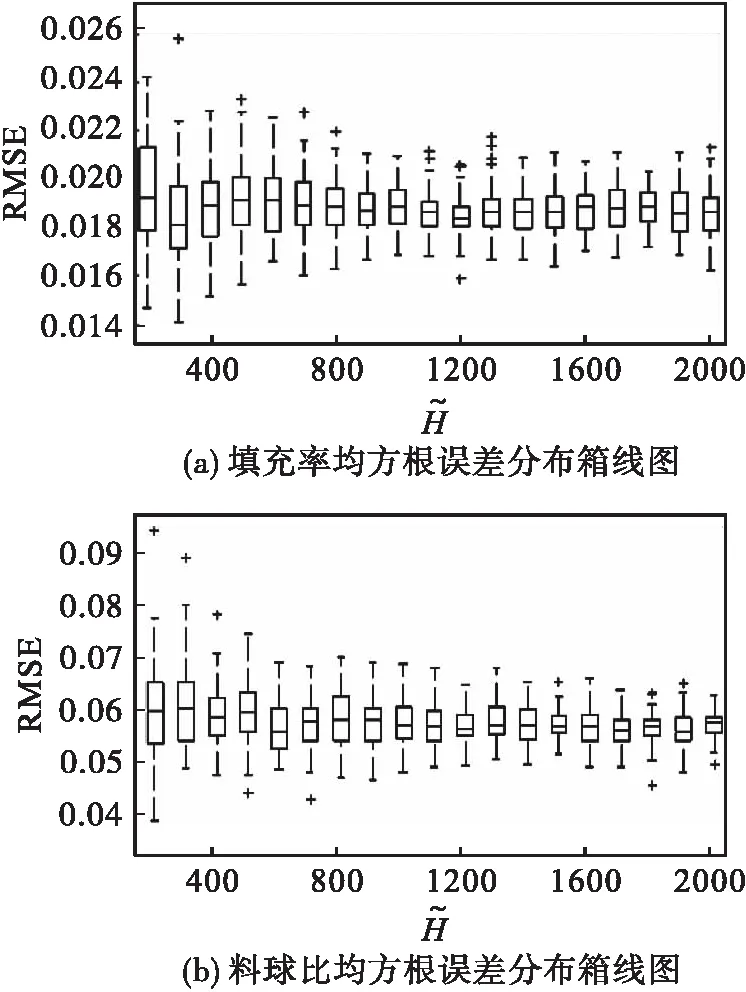
图4 填充率、料球比均方根误差分布箱线图Fig.4 Box plots of filling proportion and ball/powder weight ratio RMSE

采用KPCA，PCA，PLS分别对振动频谱进行特征分析，建立填充率和料球比的KPCA，PCA，PLS特征ELM模型，直接ELM模型和PLS模型，并对参数进行预报，将预测值与真实值进行对比.表3为不同方法下填充率预报结果的误差值大小.结果显示：不同模型的误差值存在一定差异，其中以KPCA_ELM模型的RMSE和RRMSE为最小，预报值更接近真实值.

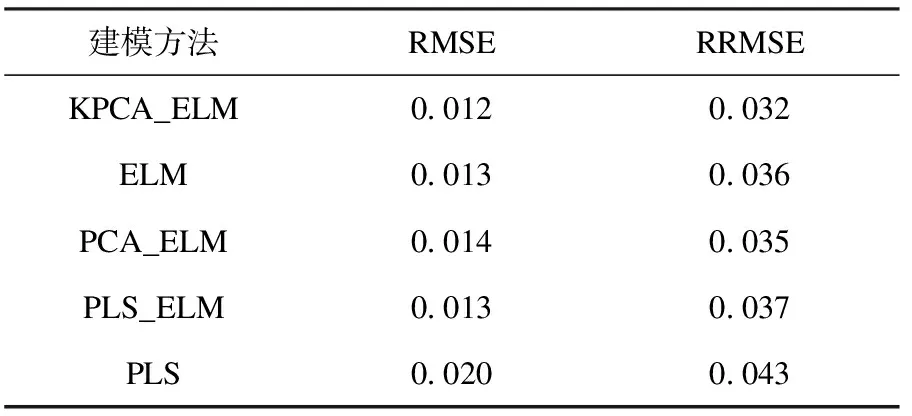
表3 不同方法填充率预报结果误差Table 3 RMSE and RRMSE of grinding density with different method

表4为不同方法下料球比预报结果与真实值误差值的大小.在5种方法中，以KPCA_ELM模型的均方根误差RMSE最小，且有一个较小的RRMSE.

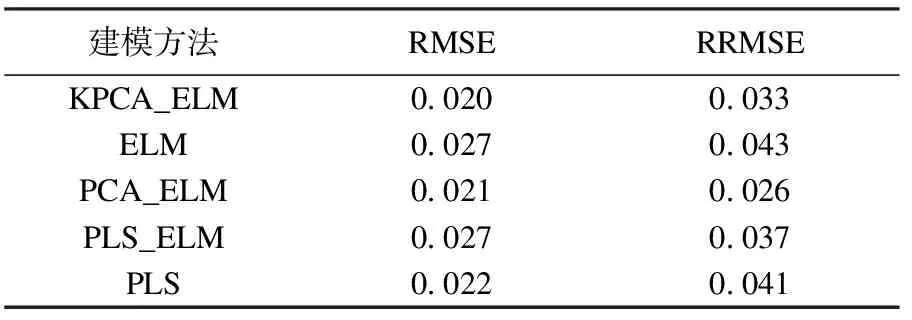
表4 不同方法料球比预报结果误差Table 4 RMSE and RRMSE of grinding density with different method

不同模型的填充率预报值与真实值的对比结果见图5，料球比对比结果见图6.由图5、图6可知：各模型的预报结果均在相同范围，结果之间相差较小，更小的RMSE和RRMSE代表更好的模型性能.因此，拥有更小误差值的基于KPCA建立的填充率和料球比ELM模型相较于其他模型更为准确.

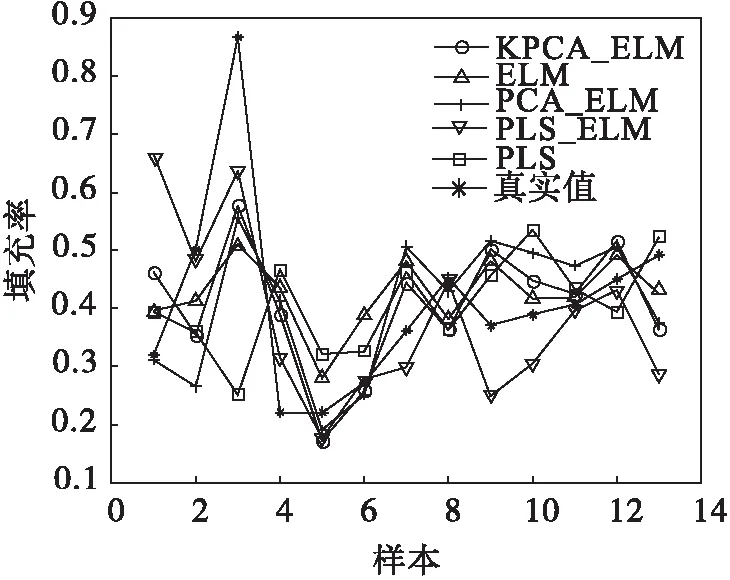
图5 填充率模型预报结果Fig.5 The prediction results of filling proportion

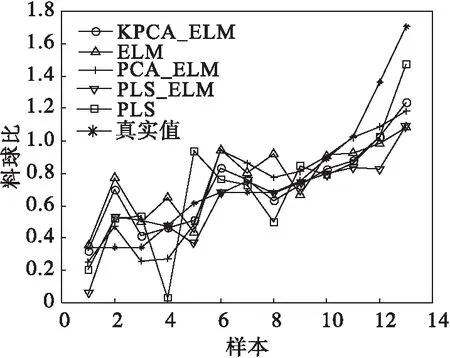
图6 料球比模型预报结果Fig.6 The prediction results of grinding density

3 结 论

针对球磨机筒体振动频谱包含大量不相关成分导致ELM预报模型准确性低的问题，采用KPCA方法对球磨机振动频谱进行特征分析，降低数据维数，提高数据有效性.以特征选择主元为输入，采用极限学习机ELM方法对球磨机的3个负荷参数磨矿浓度、料球比、填充率进行参数预报.并与基于PCA和PLS的ELM模型，直接ELM模型及PLS模型进行对比.实验结果显示:基于球磨机振动频谱KPCA特征提取结果建立的ELM模型更优于其他模型，具有更小的预报误差，软测量模型在准确性及可靠性上均有所提高.

参考文献：

[1] 徐宁,周俊武,王清.关于选矿过程智能化控制技术的探讨[J].铜业工程,2011,107(1):54-60.

[2] 冯天晶,王焕钢,徐文立,等.基于筒壁振动信号的磨机工况监测系统[J].矿冶,2010,19(2):66-69.

[3] 汤健,赵立杰,柴天佑,等.基于振动频谱的磨机负荷在线软测量建模[J].信息与控制,2012,41(1):123-128.

[4] 汤健,柴天佑,赵立杰,等.融合时/频信息的磨矿过程磨机负荷软测量[J].控制理论与应用,2012,29(5):564-570.

[5] Huang G B,Zhu Q Y,Siew C K.Extreme Learning Machine:A New Learning Scheme of Feedforward Neural Networks[C]//Proceedings of International Joint Conference on Neural Networks (IJCNN2004).Piscataway:Institute of Electrical and Electronics Engineers Inc,2004:985-990.

[6] 田慧欣,毛志忠,王嘉铮.基于ELM新方法的LF终点温度软测量混合模型[J].东北大学学报：自然科学版,2008,29(1):33-36.

[7] 肖冬,王继春,潘孝礼，等.基于改进PCA_ELM方法的穿孔机导盘转速测量[J].控制理论与应用,2010,27(1):19-24.

[8] 高海华,杨辉华,王行愚.基于PCA和KPCA特征抽取的SVM网络入侵检测方法[J].华东理工大学学报：自然科学版,2006,32(3):321-326.

[9] Schölkopf B,Smola A,Müller K R.Nonlinear Component Analysis as a Kernel Eigenvalue Problem[J].Neural computation,1998,10(5):1299-1219.

[10] JolliHe I J.Principal Component Analysis[M].New York:Springer,1986:3-10.

[11] 汤健,赵立杰,岳恒，等.基于遗传算法-偏最小二乘进行频谱特征选择的磨机负荷软测量方法[C]// 程代展,陈杰.第29届中国控制会议论文集.北京:北京航空航天大学出版社,2010:5066-5071.