基于主动自适应滑模控制的超混沌系统同步

颜闽秀,郑小帆

(沈阳化工大学 信息工程学院,辽宁 沈阳 110142)

自从1990年Pecora和Carroll提出了混沌同步的定义[1]并在电路中实现以来,混沌同步及其应用一直是研究的热点.到目前为止,各种同步方案相继提出,如完全同步[2]、反同步[3]、投影同步[4]、相同步[5]、广义同步[6]等.同时,人们提出了多种实现混沌同步的方法,如观测器同步法[7]、主动控制法[8]、自适应同步法[9]、滑模变结构同步法[10]等.在这些方法中,滑模变结构控制器因为其具有很强的鲁棒性和抗干扰能力,受到了广泛的关注.

目前,关于混沌同步的研究取得了一些研究成果.在文献[11]中,实现了具有参数不确定性、外部干扰以及非线性控制输入的混沌系统的完全同步.但是现有的研究成果大多是在混沌系统的不确定性和外部干扰的上界已知情况下实现的同步.但在实际工程应用中,上界值一般是很难或根本无法测量的[12].同时,之前大部分的研究都是针对低维数的混沌系统进行的,超混沌系统因为具有更复杂的动力学特性也受到了日益广泛的关注.

本文针对一类带未知上界的不确定性和外界扰动的超混沌系统同步问题,提出了一种新的主动自适应滑模器和参数更新规则.该规则将系统中的未知参数估计至上界,在该控制器作用下实现了两个相同或不同超混沌系统的同步和反同步.利用连续函数来替代控制律中的非连续符号函数,消除了滑模控制器的抖动问题.利用Lyapunov稳定性理论和数值仿真证明了所设计的控制器的有效性.

1 问题描述

考虑如下n维混沌系统:

式中,x,y∈Rn是系统的n维状态向量;A1,A2∈Rn×n表示系统的线性部分;f1(x),f2(y)∈Rn表示系统的非线性部分;ΔA1,ΔA2∈Rn×n描述的是系统的不确定性;u(t)是控制输入;δ1(t),δ2(t)∈Rn表示系统的外部干扰向量.

若式(1)和式(2)中A1=A2,f1(x)=f2(y),则两个系统是一致的混沌系统,否则为不同的混沌系统.定义如下误差系统:

e=y+βx.

(3)

将式(1)、式(2)代入式(3),可得误差系统为

令F(x,y)=f2(y)+βf1(x)+β(A1-A2)x,则式(4)可以表示为

通过设计加在响应系统上的控制器,使得驱动系统和响应系统达到同步,也就是要满足如下条件:

(6)

本文中,‖·‖表示Euclidean范数.

假设‖ΔA2y+βΔA1x‖<ψ,‖δ2+βδ1‖<η,其中,ψ,η为未知的正常数.

定理1 对任意的x和正数y,存在如下不等式:

xtanh(xy)=|x||tanh(xy)|≥0.

2 主动滑模控制器的设计

根据主动控制的思想,可以如下设计控制器:

u(t)=G(t)-F(x,y).

(7)

根据滑模控制律设计思想得

G(t)=Kv(t).

(8)

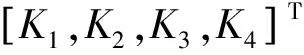
(9)

式中,s=Ce表示所设计的滑模面.

当系统在滑模面上运动时,误差系统满足如下条件:

s=Ce=0.

(10)

为了使状态轨迹到达滑模面上,可以为运动点到达切换面设计各种趋近律.较好的趋近律应该在离切换面远时,运动点向切换面运动的速度大,而接近切换面时,其速度渐近趋于零.现在运用最多的趋近律是指数趋近律:

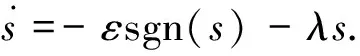
(11)

式中,ε,λ均为正实数.在常规的滑模算法中存在严重的抖动现象,为了消除控制器输出的抖动,利用连续函数tanh来替代控制律中的非连续符号函数,则有

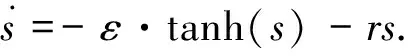
(12)

根据式(5)、式(8)和式(12)可得

则

由于系统中存在不确定项,且不确定项的上界值未知,控制器无法实现,因此,采用主动滑模控制与自适应控制相结合来设计控制器.

定理2 对于同步误差系统(6),在控制器u(t)的作用下,能够实现同步或反同步.其中

证明 选取如下正定的函数:

(16)

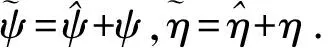
对时间t求导得

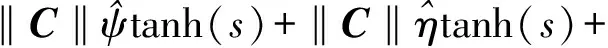
εtanh(s)+rs]+ΔA2y+βΔA1x+

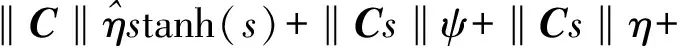
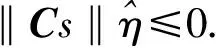
(17)

3 仿真分析与讨论

为了验证所设计的修正投影同步控制器的有效性,本文选取超混沌Lorenz系统和Chen系统为例进行研究.

超混沌Lorenz系统可以用如下方程来表示:

(18)

超混沌Chen系统可以用如下方程来表示:

(19)

式中,a=35,b=7,c=12,d=3,r=0.5.

3.1 超混沌Chen系统的同步

假设

(20)

(21)

则驱动系统为

(22)

响应系统可以写成

(23)

同步误差系统为

(24)

令ψ(0)=50,η(0)=50,C=(0,2,1,-1)T,K=(1,1,0,1),则滑模面为

s=2e2+e3-e4.

(25)

假设驱动系统的初始值为(x1(0),x2(0),x3(0),x4(0))=(1,2,-1,2),响应系统的初始值为(y1(0),y2(0),y3(0),y4(0))=(-2,5,-1,2).

图1是在控制器作用下,驱动系统和响应系统的状态响应曲线.显然,响应系统能够跟随驱动系统并达到很好的同步效果.图2表示的是本文设计的控制器的输出,图3表示的是传统滑模控制器的输出.从仿真结果可知,所设计的控制器在达到很好的同步效果的同时还解决了传统滑模控制器的严重过抖动问题.图4和图5表示的是自适应律η和ψ随时间的变化曲线.

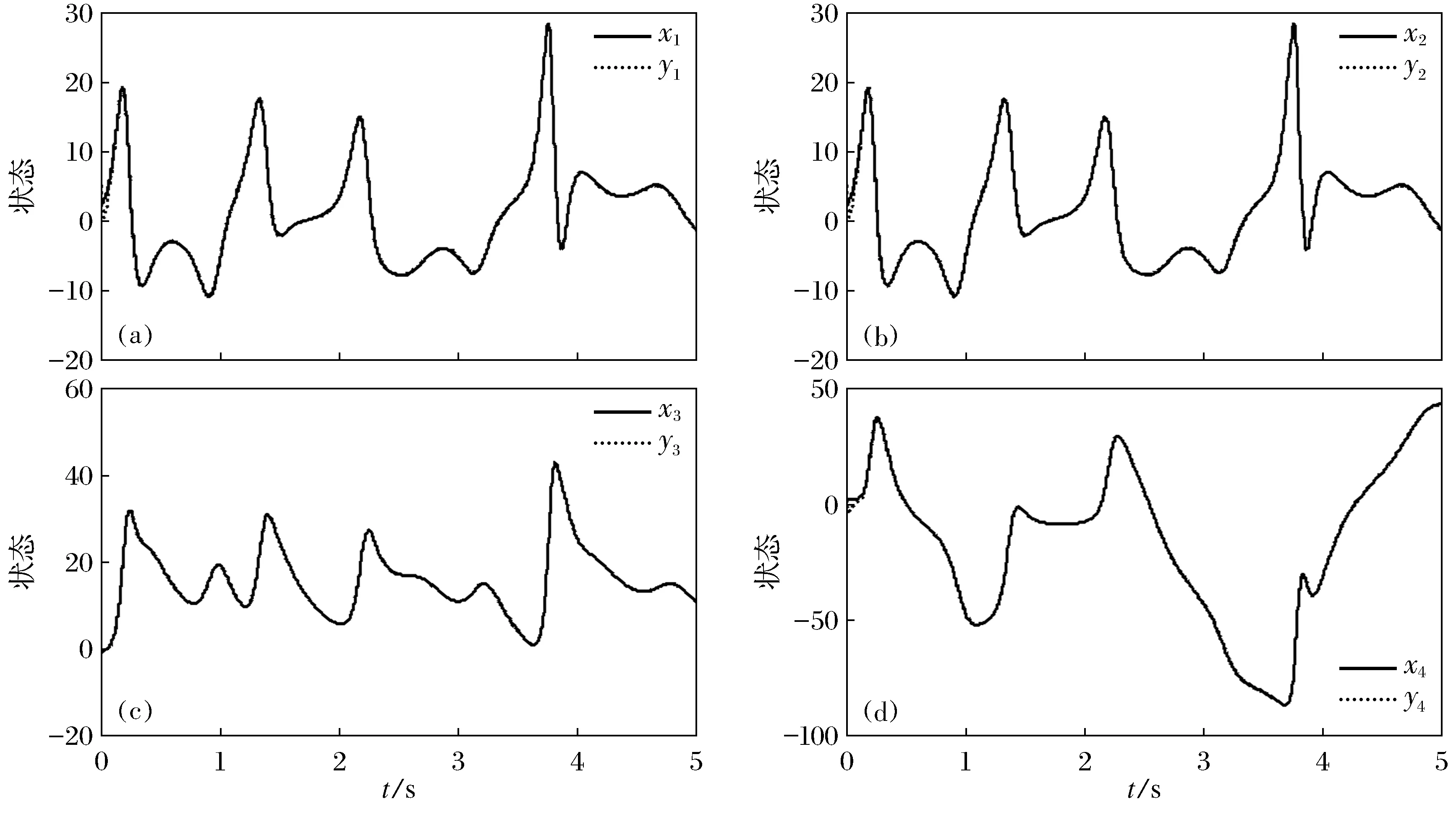
图1 驱动系统和响应系统的状态响应曲线Fig.1 State response curve of drive system and response system(a)—x1和y1的状态响应曲线;(b)—x2和y2的状态响应曲线;(c)—x3和y3的状态响应曲线;(d)—x4和y4的状态响应曲线.

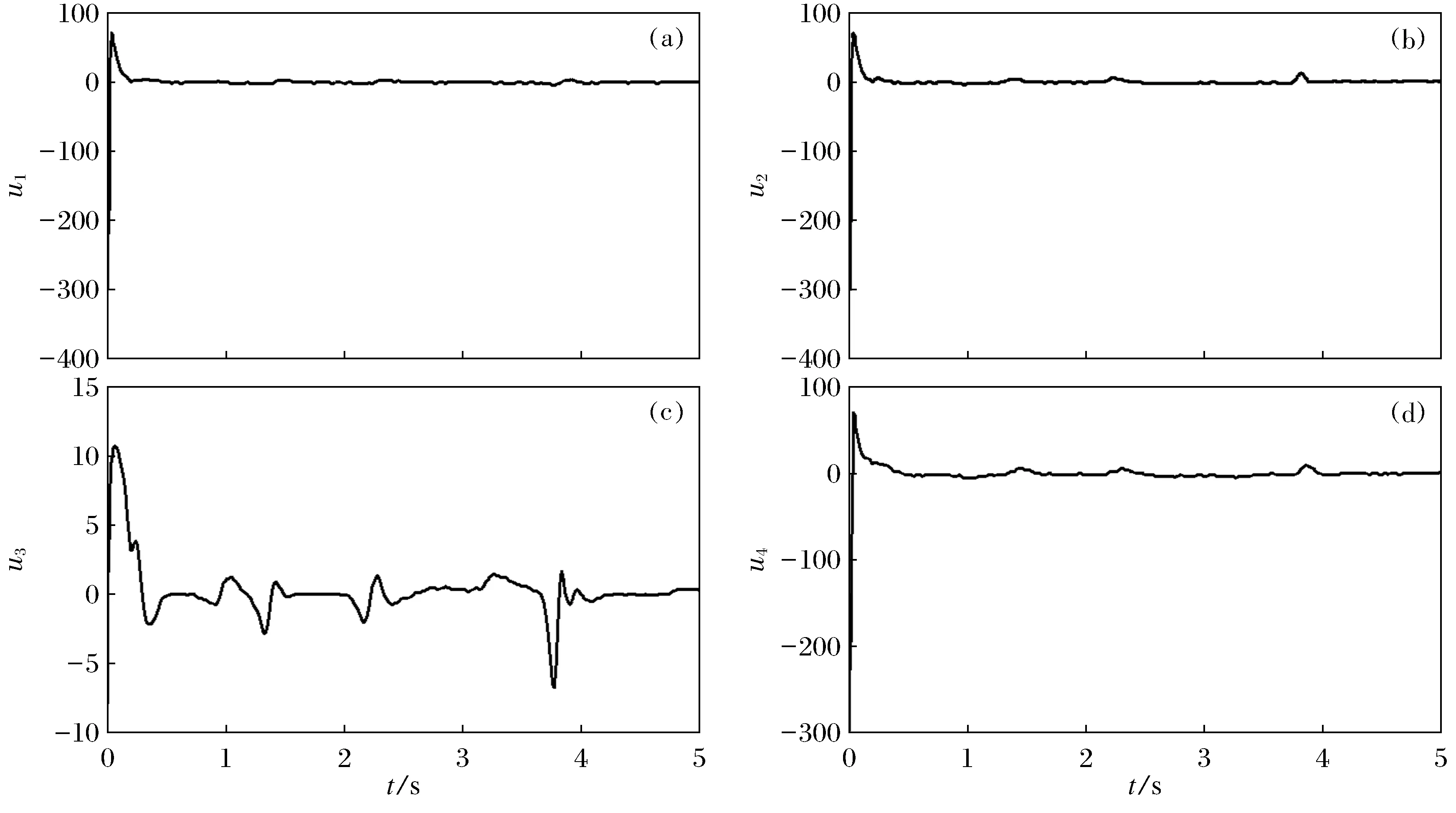
图2 本文设计的控制器的输出Fig.2 Output of the designed controller(a)—控制器u1的输出;(b)—控制器u2的输出;(c)—控制器u3的输出;(d)—控制器u4的输出.

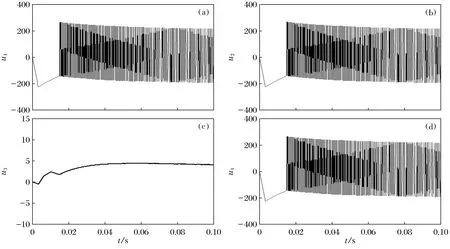
图3 传统滑模控制器的输出Fig.3 Output of traditional sliding mode controller(a)—控制器u1的放大输出;(b)—控制器u2的放大输出;(c)—控制器u3的放大输出;(d)—控制器u4的输出.

图4 自适应律η的时间响应曲线Fig.4 Time response curve of the adaptive law η

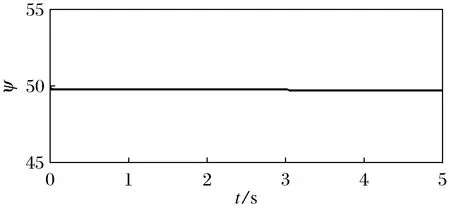
图5 自适应律ψ的时间响应曲线Fig.5 Time response curve of the adaptive law ψ

3.2 超混沌Lorenz系统和 Chen系统的反同步

假设

(26)

(27)

则驱动系统为

(28)

响应系统可以写成

(29)

同步误差系统为

(30)

令ψ(0)=50,η(0)=50,C=(0,2,1,-1),K=(1,1,0,1)T,则滑模面为

s=2e2+e3-e4.

(31)

假设驱动系统的初始值为(x1(0),x2(0),x3(0),x4(0))=(1,2,-1,2) ,响应系统的初始值为(y1(0),y2(0),y3(0),y4(0))=(-2,2,-1,2).

图6为驱动系统和响应系统的状态响应曲线,图7为本文设计的控制器的输出,图8为传统滑模控制器的输出,图9为自适应律η的时间响应曲线,图10为自适应律ψ的时间响应曲线.

从仿真结果可以看出,尽管超混沌系统受到了外部干扰,但在所设计的控制器作用下,误差状态曲线仍能渐近收敛到零.在达到同步的前提下,与传统滑模控制器相比,不存在严重的抖动问题.

图6 驱动系统和响应系统的状态响应曲线Fig.6 State response curve of drive system and response system(a)—x1和y1的状态响应曲线;(b)—x2和y2的状态响应曲线;(c)—x3和y3的状态响应曲线;(d)—x4和y4的状态响应曲线.

图7 本文设计的控制器的输出Fig.7 Output of the designed controller(a)—控制器u1的输出;(b)—控制器u2的输出;(c)—控制器u3的输出;(d)—控制器u4的输出.

图8 传统滑模控制器的输出Fig.8 Output of traditional sliding mode controller

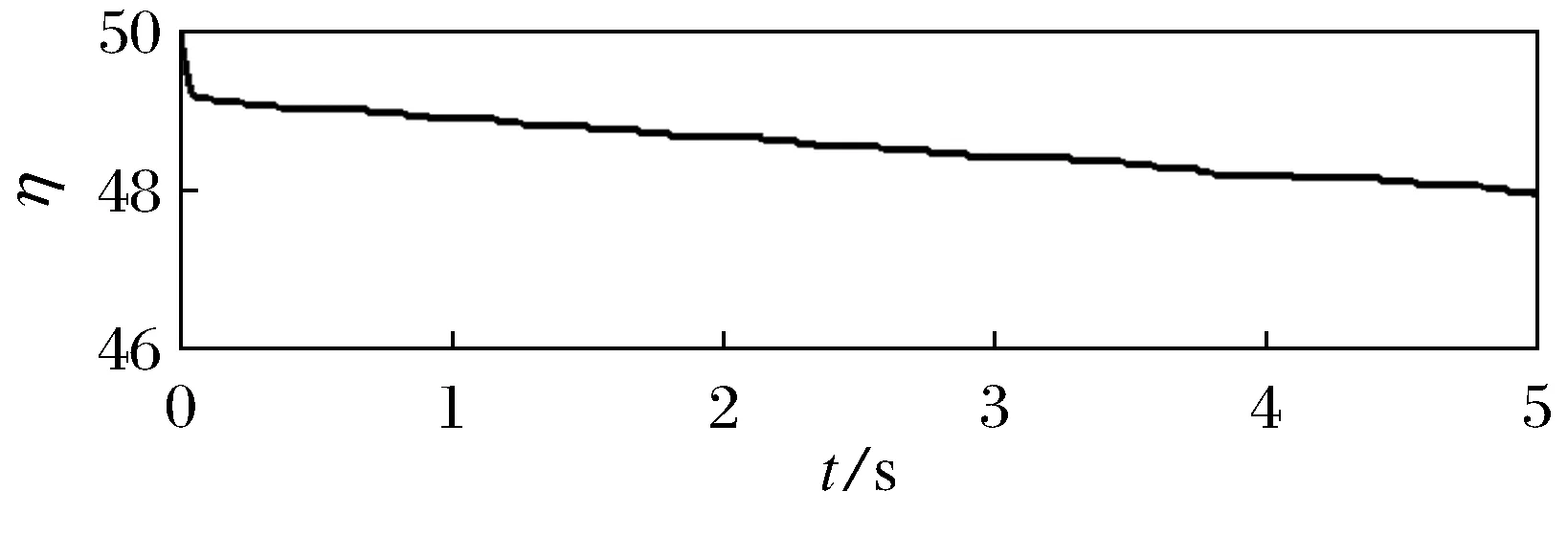
图9 自适应律η的时间响应曲线Fig.9 Time response curve of the adaptive law η

图10 自适应律ψ的时间响应曲线Fig.10 Time response curve of the adaptive law ψ

4 结 语

本文针对一类带未知上界的不确定性和外界扰动的超混沌系统同步问题,利用Lyapunov稳定理论,设计了主动自适应滑模控制器并给出了参数自适应律的表达式,并将这种混沌系统同步方法应用于超混沌Lorenz系统和Chen系统中,实现了超混沌系统的同步和反同步,通过数值仿真验证了所设计的控制器的实用有效性.

参考文献:

[1] Pecora L M,Carroll A T L.Synchronization in Chaotic Systems[J].Physical Review Letters,1990,64(8):821-824.

[2] 谭文,蒋逢灵,王耀南,等.一类混沌系统的滑动模态同步控制及其应用[J].计算机工程与应用,2013,49(7):232-234,257.

(Tan Wen,Jiang Fengling,Wang Yaonan,et al.Synchronization for a Class of Chaotic Systems Using Sliding Mode Controller and Its Application[J].Computer Engineering and Applications,2013,49(7):232-234,257.)

[3] 刘福才,贾亚飞,任丽娜.基于混沌粒子群优化算法的异结构混沌反同步自抗扰控制[J].物理学报,2013,62(12):120509(1-8).

(Liu Fucai,Jia Yafei,Ren Lina.Anti-Synchronizing Different Chaotic Systems Using Active Disturbance Rejection Controller Based on the Chaos Particle Swarm Optimization Algorithm[J].Acta Physica Sinica,2013,62(12):120509(1-8).)

[4] 颜闽秀,樊立萍.混沌系统的主动自适应滑模修正投影同步[J].自动化仪表,2013,34(2):23-25,29.

(Yan Minxiu,Fan Liping.Active Adaptive Sliding Mode Modified Projective Synchronization of the Chaotic Systems[J].Process Automation Instrumentation,2013,34(2):23-25,29.)

[5] Ho M C,Hung Y C,Chou C H.Phase and Anti-phase Synchronization of Two Chaotic Systems by Using Active Control[J].Physics Letters A,2002,296(1):43-48.

[6] 高远,翁甲强,罗晓曙,等.超混沌电路的广义同步[J].电子与信息学报,2002,24(6):855-859.

(Gao Yuan,Weng Jiaqiang,Luo Xiaoshu,et al.Generalized Synchronization of Hyperchaotic Circuit[J].Journal of Electronics and Information Technology,2002,24(6):855-859.)

[7] 姚利娜,高金峰,廖旎焕.实现混沌系统同步的非线性状态观测器方法[J].物理学报,2006,55(1):35-41.

(Yao Lina,Gao Jinfeng,Liao Nihuan.Synchronization of a Class of Chaotic Systems Using Nonlinear Observers[J].Acta Physica Sinica,2006,55(1):35-41.)

[8] Yassen M T.Chaos Synchronization between Two Different Chaotic Systems Using Active Control[J].Chaos,Solitons &Fractals,2005,23(1):131-140.

[9] Li Xianfeng,Leung A C S,Han Xiuping,et al.Complete (anti-) Synchronization of Chaotic Systems with Fully Uncertain Parameters by Adaptive Control[J].Nonlinear Dynamics,2011,63(1/2):263-275.

[10] 高远,罗文广,戴喜生,等.不确定性超混沌系统的积分滑模同步控制研究[J].自动化仪表,2012,33(5):15-17,21.

(Gao Yuan,Luo Wenguang,Dai Xisheng,et al.Research on the Integral Sliding Mode Synchronous Control of Uncertainty Hyper-Chaos System[J].Process Automation Instrumentation,2012,33(5):15-17,21.)

[11] Li Wanglong,Chang Kuoming.Robust Synchronization of Drive-Response Chaotic Systems via Adaptive Sliding Mode Control[J].Chaos,Solitons &Fractals,2009,39(5):2086-2092.

[12] 郭祥贵.一类连续非线性系统的动态输出反馈H∞控制器设计[J].沈阳大学学报:自然科学版,2012,24(5):62-68.

(Guo Xianggui.Dynamic Output FeedbackH∞Controller Design for a Class of Continuous-Time Nonlinear Systems[J].Journal of Shenyang University: Natural Science,2012,24(5):62-68.)