状态依赖下不确定切换线性系统有限时间稳定性分析
2014-03-25王跃华孙晓靓
王跃华,孙晓靓
(1.沈阳大学 理学院,辽宁 沈阳 110044;2.辽宁水利职业学院,辽宁 沈阳 110122)
对于现有的关于切换系统稳定性的研究成果,近些年主要侧重在Lyapunov渐近稳定问题上,也就是表现在无限的时间间隔里系统达到稳定.然而在实际应用中,人们更多地考虑的是在一定时间间隔内系统的各种行为.因此,从实际角度出发,人们侧重于研究的是系统的有限时间稳定问题.有限时间稳定性问题在文献[1]中初次被提及.具体地说,系统的有限时间稳定也就是要满足当系统的初始条件有界时,在有限时间内系统的状态可以达到预先设定的界限.显然,这与Lyapunov渐近稳定是不同的.一个系统可以是有限时间稳定的但是又未必是渐近稳定的,这在文献[2]中被提到,并且有限时间稳定的一些早期的结论可以在文献[3-5]中找到.
1 问题的提出与带有不确定项的切换线性系统的描述
考虑一系列如下形式的切换线性控制系统:
对于系统(1),选取如下切换状态反馈控制器:
u(t)=Kσ(t)x(t).
(3)
将式(3)代入切换线性系统(1),就可以得到如下形式的闭环系统:
2 相关假设与引理
假设1x(t)的曲线是处处连续的,也就是切换线性系统的状态x(t)在切换的瞬间是不会发生跳跃的.
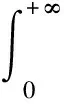
为了确定切换子系统的Lyapunov类函数,整个状态空间Rn需要被分割成若干个子空间,记作Ωi.为了达到这个目的,需要使这些Ωi区域覆盖整个状态空间,也就是需要满足如下覆盖条件:
Ω1∪Ω2∪…∪Ωm=Rn.
(4)
为了简化问题,这里假设每个区域Ωi都可以表示成如下二次形式:
Ωi={x∈Rn|xTQix≥0} (i=1,2,…,m).
(5)
式中,Qi∈Rn×n是对称矩阵.
下面的引理给出了满足覆盖条件的一种有效方法.
引理1[6](覆盖条件) 如果对于每一个状态x∈Rn,都有
(6)
成立,那么Ω1∪Ω2∪…∪Ωm=Rn.其中,θi≥0(i=1,2,…,m).
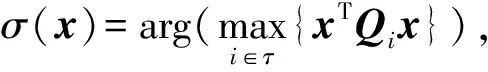
3 有限时间稳定的定义
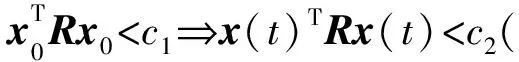
4 有限时间稳定的充分条件及证明
对于系统(1),选取切换状态反馈控制器u(t)=Kσ(t)x(t),将其代入切换线性系统(1),就可以得到如下形式的闭环系统:
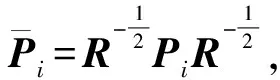
(11)
(12)
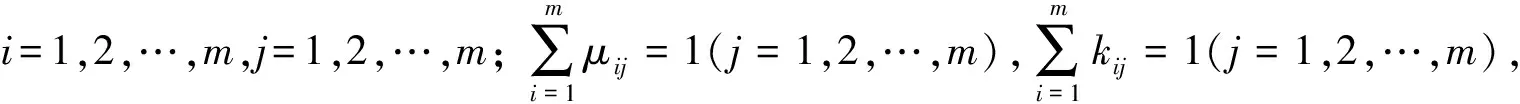
证明 令
V(x)=Vi(x)=xTPix
(13)
作为Lyapunov备选函数用来测量每一个区域Ωi的能量.这里不妨设i=1,2;j=1,2.对于i,j为其他值的一般情况也是显然的.
第一种情况:当滑膜现象不发生时.
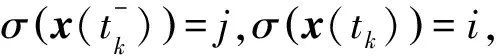
(14)
由式(7)可得
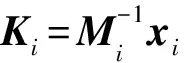
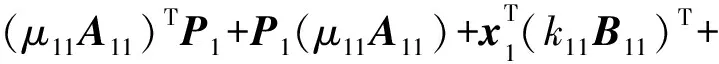
(k11B11)x1+(μ12A12)TP1+P1(μ12A12)+
(19)
(k21B21)x2+(μ22A22)TP2+P2(μ22A22)+
(20)

(21)
对其从tk到t求解可得
V(x) (22) (23) 由式(21)和式(22)可以得到 根据式(10)以及式(24)~式(26)可以得到 (27) 则根据定义可知,连续时间切换线性系统(1)是有限时间稳定的. 第二种情况:当滑膜现象发生时. 当滑膜现象发生时,在状态处满足如下关系式: 也就是在子系统发生变化时会产生滑膜现象.滑膜现象可能在区域Ωi,j处发生,也就是满足如下关系式: xTQix=xTQjx≥0. 滑膜现象会导致在切换表面产生或者稳定或者不稳定的动力系统,因此,需要研究定理中给定的条件是否能够保证在滑膜现象发生时切换系统仍然是有限时间稳定的.当滑膜现象在超平面Ωi,j处发生时,也就意味着满足如下关系式: 式中:i=1,2,…,m,j=1,2,…,m.也就是要满足如下关系式: 因此,在滑膜表面的系统可以表示成 其中,ρ∈[0,1].由定理中的不等式可得 由此可得 式(33)和式(34)相加可得 同时有 式(36)和式(37)相加可得 αxTλ3x<αxTPjx. (38) 从而可以得到 (39) 也就是 (40) 因为式(21)和式(29)同样适用于滑膜表面的系统,因此,剩下的证明过程和第一种情况相同. 本文主要研究了在状态依赖切换策略下,带有不确定项的切换系统的有限时间稳定性问题.与以往的文献侧重于运用时间依赖切换策略相比,本文研究的状态依赖切换策略更加复杂,由于切换常数有时不会事先给出,因此,本文研究的状态依赖切换策略就显得更加实用. 参考文献: [1] Dorato P.Short Time Stability in Linear Time-Varying Systems[C]∥Proceedings of the IRE International Convention Record: Part 4.New York,1961:83-87. [2] Amato F,Ariola M,Dorato P.Finite-Time Control of Linear Systems Subject to Parametric Uncertainties and Disturbances[J].Automatica,2001,37(9):1459-1463. [3] Weiss L,Infante E.Finite Time Stability under Perturbing Forces and on Product Spaces[J].IEEE Transactions on Automatic Control ,1967,12(1):54-59. [4] Li Shihua,Wang Zhao,Fei Shumin.Finite-Time Control of a Bioreactor System Using Terminal Sliding Mode[J].International Journal of Innovative Computing,Information and Control ,2009,5(10B):3495-3504. [5] He Shuping,Liu Fei.Robust Finite-Time Stabilization of Uncertain Fuzzy Jump Systems[J].International Journal of Innovative Computing,Information and Control,2010,6(9):3853-3862. [6] Pettersson S.Synthesis of Switched Linear Systems[C]∥Proceedings of the 42nd IEEE Conference on Decision and Control.Maui,2003:5283-5288. [7] Zhao Guanglei,Wang Jingcheng.Finite Time Stability and L2-gain Analysis for Switched Linear Systems with State-Dependent Switching[J].Journal of the Franklin Institute,2013,350(5):1075-1092.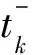
5 结 语
