二机流水作业带不可用区间、工件可拒绝的调度问题
2014-03-25孔祥玉郑勇跃
谢 谢,孔祥玉,郑勇跃
(1.沈阳大学 装备制造综合自动化重点实验室,辽宁 沈阳 110044;2.辽宁省标准化研究院,辽宁 沈阳 110004)
大多数的调度问题都是在经典调度模型的基础上进行研究的,如文献[1],工件的拒绝是不允许的.但有时会因为原材料的限制使得人们不得不拒绝某些工件的加工,或者一些生产商为了获得更大的利润,会选择拒绝一些由于加工时间较长而带来整体效益减少的工件.无论出于何种原因拒绝工件的加工,支付一定的惩罚是必不可少的.针对不可用区间的约束经常在生产企业出现,产生的原因主要分为两大类型:第一种是确定性的不可用,即由于机器的维护保养带来的一段确定的时间内机器不能加工任何工件;第二种是随机性的不可用,即由于机器意外破损导致的机器在一段时间内不能加工任何工件,出现这种情况时,调度人员不能事先预知不可用具体在哪一时段发生.无论是由于何种原因带来的不可用,都要做好准备,避免由于停工带来的利益损失.本文将加工机器具有不可用区间、工件可拒绝的约束集成考虑,最小化可接受加工工件的最大完工时间与拒绝工件的惩罚之和.
Adiri等[2]首次研究了带有不可用区间的单机调度问题,分别针对具有确定性的不可用区间和随机性的不可用区间两种情况进行了研究,目标是最小化工件的完工时间和.Lee和Liman[3]与Adiri等[2]考虑了同样的问题,并证明了带有确定不可用区间的该问题是NP-难的,提出了启发式算法并给出了紧界.Ng和Kovalyov[4]研究了二机流水作业带有一个确定的不可用区间的问题,分别针对不可用区间在第一台机器上产生和在第二台机器上产生提出了启发式算法,并提出了全多项式时间近似方案(FPTAS).Lee[5]研究了带有不可用区间的平行机调度问题,目标是最小化加工工件的完工时间,应用LPT算法求解了此问题,证明了该算法的最坏性能比为3/2,并进一步修改了该LPT算法,证明了它的最坏性能比是4/3.Lee和Liman[6]研究了两台机器的平行机调度问题,其中一台机器上带不可用区间,提出了动态规划算法并给出了问题的最优解.Lee[7]研究了二机流水作业带不可用区间的调度问题,分别针对不可用区间在第一台机器和第二台机器上两种情况作出了分析,分别给出了启发式算法和动态规划算法.
工件可拒绝的调度问题是由Bartal等[8]首次提出的,主要针对混合机带有工件加工可拒绝的调度问题,目标是最小化接受工件的时间表长与拒绝工件的惩罚之和.Hoogeveen等[9]研究了工件加工可拒绝的平行机(同类机、同速机、变速机)调度问题,提出了一个1.58-因子算法.Dósa和He[10]研究了机器花费且带有拒绝工件的问题,在他们的模型中,一开始没有一个确定的机器花费,只有当购买新机器时这种花费才可以确定.
1 问题参数及描述

2 动态规划算法
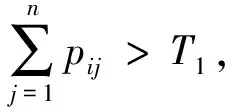
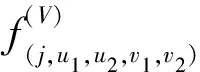
对于工件Jj,存在三种情况:工件Jj被拒绝;工件Jj接受加工并且在T1前加工完成;工件Jj接受加工并且在T2后加工完成.
情况1 若Jj被拒绝,则有下式成立:

情况2 若Jj接受加工且在T1前加工完成,则有下式成立:
情况3 若Jj接受加工且在T2后加工完成,则有下式成立:
综合上述3种情况,给出如下动态规划算法.
(1) 边界条件:当j=1时
(2) 动态规划递推函数:当j=2,…,n时
其中各参数满足如下条件:
其中,JA是最初应用Johnson算法排序的目标值.
此动态规划算法是在所有参数的取值范围内求得问题的最优解.下面给出数值实例并应用动态规划的迭代过程得到问题的最优解.
给定工件的个数n=4,不可用区间[T1,T2]=[3,4],各工件分别在M1和M2上的加工时间与惩罚值如表1所示.

表1 各工件分别在M1和M2上的加工时间与惩罚值Table 1 Processing time and penalty value of each workpiece on M1 and M2
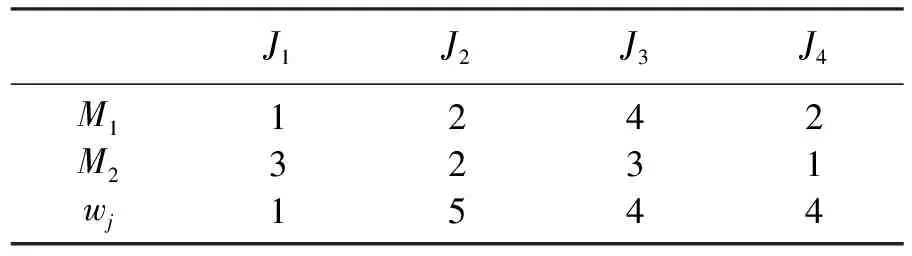
表2 相应的各参数Table 2 Corresponding parameters
按照工件的个数划分为四个阶段,k=1,2,3,4.
(1) 第一次迭代,即当k=1时,分为四大类情况.
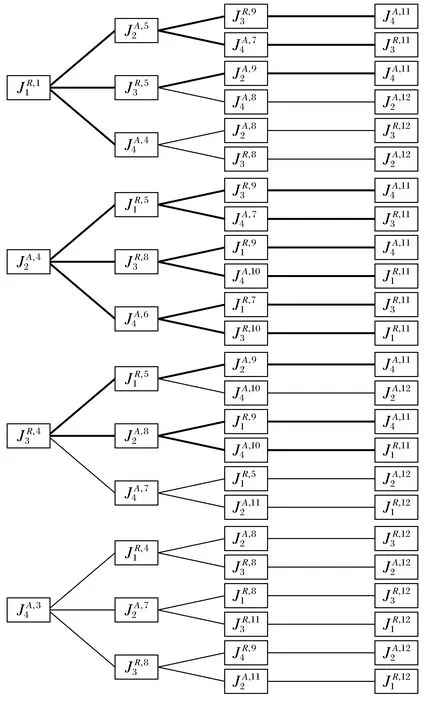
① 考虑工件J1是接受加工还是拒绝加工.因为p11=1 =1, 所以工件J1被拒绝加工. ② 考虑工件J2是接受加工还是拒绝加工.因为p12=2 =4. 所以工件J2接受加工. ③ 考虑工件J3是接受加工还是拒绝加工.因为p13=4>T1=3,工件J3在T2后完工,有 =4. 所以工件J3拒绝加工. ④ 考虑工件J4是接受加工还是拒绝加工.因为p14=2 =3. 所以接受工件J4. (2) 第二次迭代,即当k=2时,在前一阶段工件J1被拒绝的情况下,考虑剩余3个工件是接受加工还是拒绝加工,有 此时工件J2接受加工,J3拒绝加工,J4接受加工. 同理,在工件J2接受加工的情况下,考虑工件J1,J3,J4的加工情况,有 所以拒绝J1加工,拒绝J3加工,接受J4加工. 根据以上分析过程,依次考虑当J3拒绝加工和J4接受加工时其余工件的加工情况.当J3拒绝加工时,其余工件的加工情况为:工件J1拒绝加工,目标值为5;工件J2接受加工,目标值为9;工件J4接受加工,目标值为7.当J4接受加工时,其余工件的加工情况为:工件J1拒绝加工,其目标值为4;工件J2接受加工,其目标值为7;工件J3拒绝加工,其目标值为8. (3) 第三次迭代,即当k=3时,分为四大类情况. ① 当第一阶段工件J1拒绝且第二阶段工件J2被接受时,有 所以拒绝工件J3,其目标值为9;接受工件J4,其目标值为7. 依据上述分析过程,当第二阶段工件J3拒绝加工时,接受工件J2,其目标值为9;接受工件J4,其目标值为8.当第二阶段接受工件J4时,接受工件J2,其目标值为8;拒绝工件J3,其目标值为8. ② 当第一阶段工件J2接受加工且第二阶段工件J1拒绝加工时,在第三阶段拒绝工件J3,其目标值为9;接受工件J4,其目标值为7.当第一阶段工件J2接受加工且第二阶段工件J3拒绝加工时,在第三阶段拒绝工件J1,其目标值为9;接受工件J4,其目标值为10.当第一阶段工件J2接受加工且第二阶段接受工件J4加工时,在第三阶段拒绝工件J1,其目标值为7;拒绝工件J3,其目标值为10. ③ 当第一阶段工件J3拒绝加工且第二阶段工件J1拒绝加工时,在第三阶段接受工件J2,其目标值为9;接受工件J4,其目标值为10.当第一阶段工件J3拒绝加工且第二阶段接受工件J2加工时,在第三阶段拒绝工件J1,其目标值为9;接受工件J4,其目标值为10.当第一阶段工件J3拒绝加工且第二阶段接受工件J4加工时,在第三阶段拒绝工件J1,其目标值为5;接受工件J2,其目标值为11. ④ 当第一阶段工件J4接受加工且第二阶段工件J1拒绝加工时,在第三阶段接受工件J2,其目标值为8;拒绝工件J3,其目标值为8.当第一阶段工件J4接受加工且第二阶段接受工件J2加工时,在第三阶段拒绝工件J1,其目标值为8;接受工件J3,其目标值为11.当第一阶段工件J4接受加工且第二阶段拒绝工件J3加工时,在第三阶段拒绝工件J1,其目标值为9;接受工件J2,其目标值为11. (4) 第四次迭代,即当k=4时,当第一阶段拒绝J1、第二阶段接受J2、第三阶段拒绝J3、第四阶段需考虑是否加工J4时,有 =11, 所以接受工件J4加工. 图1 数值实例的动态规划示意图Fig.1 Dynamic programming schematic of numerical example 综上所述,最优解为拒绝工件J1,J3,接受工件J2,J4,并按此顺序依次在机器上加工,且最优值为11. 由于动态规划算法可以在短时间内求解小规模问题,并得到最优值,随着问题规模的增大,计算时间成指数增长,因此,为了克服动态规划算法的缺陷,本文提出了一个多项式时间内可解的启发式算法并对它的最坏性能进行了分析. 第1步 首先使用Johnson算法对所有的工件进行调度,相应的调度记为σ1,并计算调度目标值为Cmax(σ1). 第3步 按照第2步的加工顺序加工工件,将Jk放在第一位加工,相应的调度记为σ3,目标值记为Cmax(σ3). 第4步 选择已得到的目标值Cmax(σ1),Cmax(σ2),Cmax(σ3)中最小的,将其调度记为σH. 证明 由于 本文研究的是二机流水作业带有不可用区间、工件可拒绝的问题,该问题已证明是NP-难的.首先提出了动态规划算法以求解小规模问题的最优解,随着问题规模的扩大,算法的运算时间变长,为了克服动态规划在计算时间上的缺陷,进一步提出了一个启发式算法以获得近似解.通过最坏性能分析可知,算法的性能比是3.未来的研究将进一步对具有更多相关约束的实际问题提出多项式时间内可解的近似策略,并将研究推广到多台机器具有类似约束的问题. 参考文献: [1] 谢谢,李彦平.带有单服务器的并行机调度问题[J].沈阳大学学报:自然科学版,2012,24(4):66-69. (Xie Xie,Li Yanping.Scheduling Parallel Machines with a Single Server[J].Journal of Shenyang University: Natural Science,2012,24(4):66-69.) [2] Adiri I,Bruno J,Frostig E,et al.Single Machine Flow-Time Scheduling with a Single Breakdown[J].Acta Informatica,1989,26(7):679-696. [3] Lee C Y,Liman S D.Single Machine Flow-Time Scheduling with Scheduled Maintenance[J].Acta Informatica,1992,29(4):375-382. [4] Ng C T,Kovalyov M Y.An FPTAS for Scheduling a Two-Machine Flowshop with One Unavailability Interval[J].Naval Research Logistics,2004,51(3):307-315. [5] Lee C Y.Parallel Machine Scheduling with Non-Simultaneous Machine Available Time[J].Discrete Applied Mathematics,1991,30(1):53-61. [6] Lee C Y,Liman S D.Capacitated Two-Parallel Machine Scheduling to Minimize Sum of Job Completion Times[J].Discrete Applied Mathematics,1993,41(3):211-222. [7] Lee C Y.Minimizing the Makespan in the Two-Machine Flowshop Scheduling Problem with an Availability Constraint[J].Operations Research Letters,1997,20(3):129-139. [8] Bartal Y,Leonardi S,Spaccamela A M,et al.Multiprocessor Scheduling with Rejection[J].SIAM Journal on Discrete Mathematics,2000,13(1):64-78. [9] Hoogeveen H,Skutella M,Woeginger G J.Preemptive Scheduling with Rejection[J].Mathematics Programming,2003,94(2/3):361-374. [10] Dósa G,He Yong.Scheduling with Machine Cost and Rejection[J].Journal of Combinatorial Optimization,2006,12(4):337-350.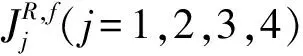
3 启发式算法及其性能分析





4 结 语
