空间几何元素一般相交问题的求解

沈丽萍, 王 刚

(1. 沈阳建筑大学 理学院, 辽宁 沈阳 110168; 2. 辽宁省水利职业技术学院, 辽宁 沈阳 110122)

1 问题的提出

《画法几何》中,直线与平面相交及平面与平面相交包括两种情况,一种是特殊情况(相交两元素至少有一个是特殊位置的),另一种是一般情况(相交两元素均为一般位置的)[1].几何问题的求解包括求交点(交线)及可见性判别.可见性判别既是问题的重点,又是问题的难点.可见性判别多采用直观法和重影点法.

1.1 特殊情况的相交

图1a为一般位置的直线(如MN)和投影面垂直面(如△ABC表示的铅垂面)相交.问题求解的目的有两个,一是求交点,二是判别可见性.

(1) 求交点.直线和平面相交,交点是直线和平面的共有点[2].△ABC表示的铅垂面的水平投影积聚成一条线段,所以交点的水平投影即是直线MN的水平投影mn与△ABC的水平投影ab的交点,如图1b所示的k点.根据从属性,由k点向上作投影连系线,与m′n′相交得交点K的正面投影k′点.

(2) 判别可见性.特殊情况的相交多采用直观法判别可见性.可见性判别即是投影可见与不可见[3].从水平投影图上可直观地看出直线和平面不存在相互遮挡.所以,直线和平面的水平投影均为实线.正面投影存在相互遮挡.判别正面投影可见与否即是判别谁在前谁在后.从水平投影出发,交点k以左的直线在平面前,所以正面投影中交点k′以左的直线段k′1′段为可见(用实线表示).根据交点是可见与不可见的分界点,得交点k′以右的直线段k′2′段为不可见(用虚线表示).如图1b所示.

图1 特殊情况的相交Fig.1 Special case of intersection

1.2 一般情况的相交

如图2a所示为一般位置的直线DE与△ABC表示的一般位置的平面相交,求交点并判别可见性.

图2 一般情况的相交Fig.2 General case of the intersection

(1) 求交点.采用辅助平面法求交点[4],作图过程如图2b所示,包含DE作铅垂面P,该铅垂面与直线AB,AC相交于点Ⅰ,Ⅱ,点Ⅰ,Ⅱ的水平投影为1,2,即1点在ab上,2点在ac上.由1,2向上作投影连系线,分别与a′b′,a′c′相交得点1′,2′,连接1′,2′与d′e′相交于点k′,点k′即是直线DE与平面△ABC的交点K的正面投影.由k′向下作投影连系线得交点K的水平投影k.

(2) 判别可见性.一般情况的相交多采用重影点法判别可见性.如图2c所示,水平投影中,ac和de的交点并不是空间两直线AC,DE的交点,在空间两直线是交叉的.水平投影的交点是分别位于AC上的Ⅱ点与DE上的Ⅲ点的水平投影的重影点.由2,3向上作投影连系线得2′,3′.2′在a′c′上,3′在d′e′上.由正面投影可知3′在上,2′在下,得Ⅲ点所从属的直线DE在Ⅱ点所从属的直线AC之上,故水平投影中k3段为可见(用实线表示),交点k另一侧k1段为不可见(用虚线表示).同理,正面投影中,Ⅴ点所位于的AC在Ⅳ点所位于的DE前,所以k′4′段为不可见,另一侧为可见.综上所述,线、面相交的可见性判别,采用的是直观法或重影点法,但直观法有其局限性,重影点法空间概念又较强,不易被理解,所以本文提出另一种解题思路----“两线相交法”,用于解决一般性相交中可见性的判别.

2 研究原理

“两线相交法”原理的提出是基于两直线相交可见性的判别.

空间两直线AB和CD相交,当相交两直线AB和CD所组成的平面的某面投影有积聚性时,两直线在该投影面上的投影重合为一条直线,在另外一个投影面上的投影相交.如图3a所示的相交两直线AB和CD所构成的平面为正垂面,正面投影有积聚性,两直线的正面投影重合,水平投影不重合.这里将从两直线某面投影相互遮挡入手,为一般位置的直线与一般位置的平面相交、两一般位置的平面相交的可见性判别提供更为直观的研究方法.

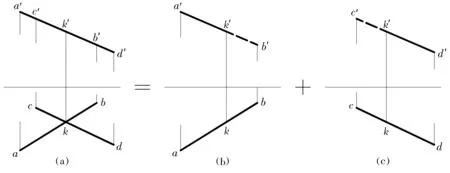
图3 两直线相交Fig.3 Intersection of two straight lines

从图3a看,直线AB和CD的水平投影ab与cd均为实线,且不存在彼此遮挡.正面投影a′b′与c′d′也为实线,直观感觉正面投影都是可见的.实际上,两直线的正面投影存在相互遮挡.将AB,CD的投影进行分解,如图3b和图3c所示.图3b为直线AB的两面投影,正面投影k′b′段为虚线,是直线CD上KD段对其遮挡;图3c为直线CD的两面投影,正面投影c′k′段为虚线,是直线AB上AK段对其遮挡.水平投影ab和cd的交点k的左侧,ak在前,ck在后,所以正面投影a′k′为实线(可见),c′k′为虚线(不可见);交点k的右侧与左侧相反.由此,将两线相交的可见性判别原理用于解决一般位置的直线与一般位置的平面、一般位置的平面与一般位置的平面相交的可见性判别中.

3 研究应用

3.1 一般位置的直线与一般位置的平面相交

如图4a所示为△ABC表示的一般位置的平面与DE表示的一般位置的直线相交,求交点并进行可见性判别.下面用“两线相交法”解决这类问题.

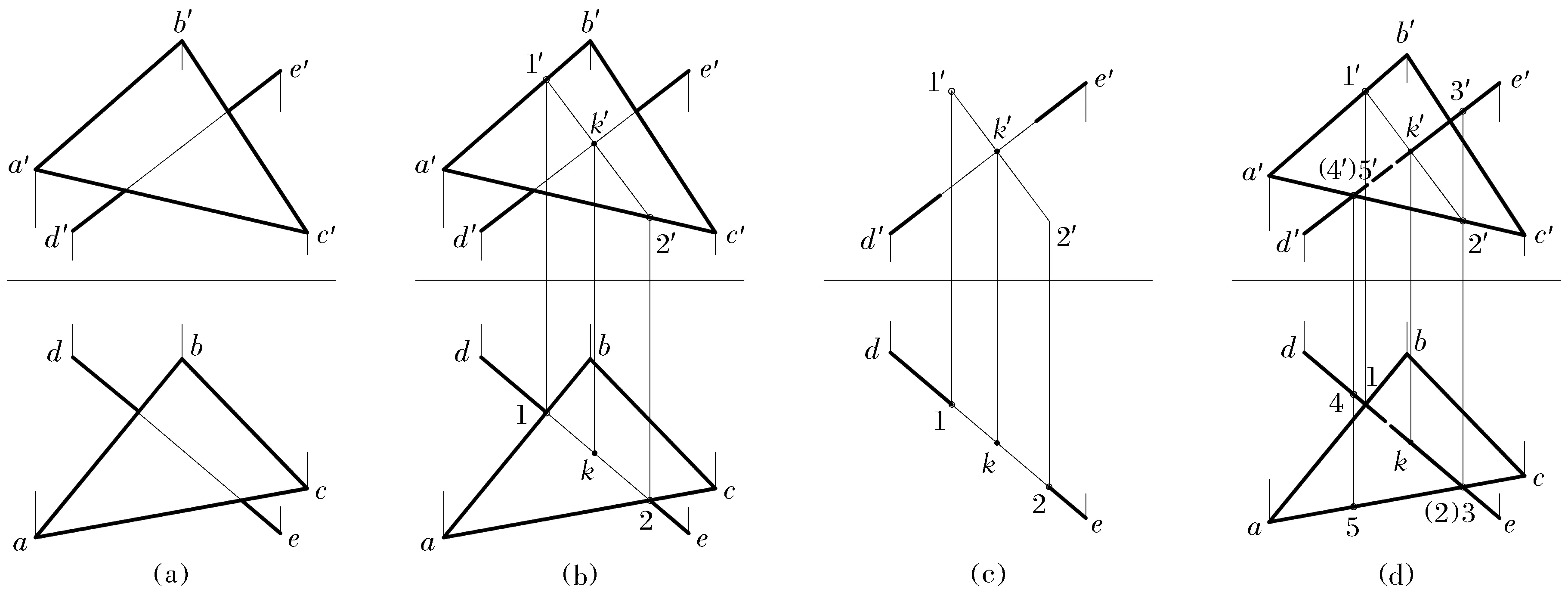
图4 一般位置的直线与一般位置的平面相交Fig.4 Intersection of a straight line in general location and a plane in general location

(1) 求交点.直线DE与平面△ABC只有一个共有的交点.如前所述的方法,通过作辅助平面得出交点K的两面投影k和k′,如图4b所示.

(2) 判别可见性.采用“两线相交法”判别可见性.

实际上,交点K是直线DE与△ABC平面内的无数条相交于同一点的直线的交点,其中必有一条直线的水平投影和直线DE的水平投影重合为一条直线,如△ABC平面内的直线ⅠⅡ与直线DE的水平投影重合为一条直线,即直线ⅠⅡ与直线DE构成的平面的水平投影有积聚性.采用“两线相交法”将直线ⅠⅡ与直线DE的两面投影单独拿出来分析,如图4c所示.由图4c可以看出,两直线的正面投影不重合,不存在相互遮挡;水平投影重合为一条直线,存在相互遮挡.从正面投影看,交点k′左侧1′2′在上,d′e′在下.所以水平投影的交点K的左侧直线DE是虚线,右侧为实线.同理,△ABC平面内也必有一条直线的正面投影和直线DE的正面投影重合,用同样的原理对直线DE的正面投影判别可见性.最后得出:一般位置的平面△ABC与一般位置的直线DE相交的交点、可见性判别投影图如图4d所示[5-6].

3.2 一般位置的平面与一般位置的平面相交

一般位置的平面与一般位置的平面相交,求交线并判别可见性,是相交类问题中的难点.“两线相交法”原理的提出,将使这个问题变得简单易行.

如图5a所示为△ABC与△DEF表示的两个一般位置的平面相交,求其交线并判别可见性.

(1) 求交线.两个一般位置的平面相交的交线的两个端点,相当于两条一般位置的直线分别和同一个一般位置的平面相交的两个交点.图5中,交线的一个端点M可看成是一般位置的直线DE与一般位置的平面△ABC相交的一个交点,交线的另一个端点N可看成是一般位置的直线DF与一般位置的平面△ABC相交的一个交点.所以可用辅助平面法求出交点M与N的两面投影,得两面交线MN的水平投影mn及正面投影m′n′,如图5b所示.

(2) 判别可见性.同前述的一般位置的直线和一般位置的平面相交,应用“两线相交法”判别两个一般位置的平面相交的可见性判别.比如,端点M是直线DE与△ABC的交点,M的水平投影是直线DE与△ABC面上的直线ⅠⅡ的水平投影的交点,即m是de与12的交点,见图5c.由图5c可见,正面投影m′的右侧m′e′在上,m′2′在下,所以水平投影的交点m的右侧me为实线.由“实—虚—实—虚—……”得水平投影[6],见图5d.同理可求出正面投影.

图5 一般位置的平面与一般位置的平面相交Fig.5 Intersection of two planes in general location

4 结 语

在以往求解空间一般位置的直线与一般位置的平面相交、空间一般位置的平面与一般位置的平面相交的可见性判别所采用的直观法和重影点法之外,本文提出另外一种新的判别理论----“两线相交法”.这是一种几何化的全新思路[7],能从理论上严格保证每一种相交情况可见性判别的正确性,使得可见性判别中较为难点的一般相交问题变得简单直观,同时也为空间其他元素相交的问题提供了新的解题思路.

参考文献:

[1]何斌,陈锦昌. 建筑制图[M]. 5版. 北京:高等教育出版社, 2005:54-55.

(He Bin, Chen Jinchang. Architectural Drawing[M]. 5th ed. Beijing: Higher Education Press, 2005:54-55.)

[2]王桂梅,远方,刘继海. 土木工程图读绘基础[M]. 3版. 北京:高等教育出版社, 2013:32-33.

(Wang Guimei,Yuan Fang, Liu Jihai. Reading and Drawing Foundation of Civil Engineering Drawing[M]. 3rd ed. Beijing: Higher Education Press, 2013:32-33.)

[3]赵大兴. 工程制图[M]. 北京:高等教育出版社, 2004:65-66.

(Zhao Daxing. Engineering Drawing[M]. Beijing: Higher Education Press, 2004:65-66.)

[4]邓学雄,太良平,梁圣复,等. 建筑图学[M]. 北京:高等教育出版社, 2007:48-53.

(Deng Xuexiong, Tai Liangping, Liang Shengfu, et al. The Engineering Graphics[M]. Beijing: Higher Education Press, 2007:48-53.)

[5]丁建梅,周佳新. 土木工程制图[M]. 北京:人民交通出版社, 2007:56-58.

(Ding Jianmei, Zhou Jiaxin. Civil Engineering Drawing[M]. Beijing: China Communications Press, 2007:56-58.)

[6]张德贤. 谈《画法几何及机械制图课》教法[J]. 沈阳大学学报, 1994(1):34-35,83.

(Zhang Dexian. On Teaching Method of “Descriptive Geometry and Mechanical Drawing” Course[J]. Journal of Shenyang University, 1994(1):34-35,83.)

[7]于海燕,何援军. 空间两三角形的相交问题[J]. 图学学报, 2013,34(4):54-62.

(Yu Haiyan, He Yuanjun. Testing the Intersection Status of Two Triangles[J]. Journal of Graphics, 2013,34(4):54-62.)