城区环境宜居性关键影响因素的系统动力学模型
2014-03-25徐洪学王婷婷
徐洪学, 王婷婷
(沈阳大学 信息工程学院, 辽宁 沈阳 110044)
城区环境问题是一个涉及面广、关系错综复杂的系统问题[1].城区宜居环境系统包括自然物质环境和社会人文环境的各方面因素[2].本文选取对城区宜居环境质量产生重大影响并具有一定代表性的关键影响因素[3-4],包括绿化率、交通便宜度、医疗技术水平、居民素质水平和商业服务质量作为研究对象,以系统动力学理论为依据并综合利用系统分析的方法[5-6],构建城区环境宜居性关键影响因素系统动力学模型,并结合沈阳市铁西区统计年鉴中提供的有效数据[7],利用参数估计方法对所构建的模型进行一致性和有效性检验,检验结果证明了所构建模型的有效性和实用性.
1 关键影响因素系统动力学模型构建
1.1 绿化率分析模型
绿化率主要是由实际绿地面积和城区总面积决定的,总面积在较长一段时间内几乎不会发生变化,可以视为常量.实际绿地面积则受到计划新增绿地面积和退化绿地面积的影响,计划新增绿地通常包括计划新增公共绿地、计划新增生产绿地和计划新增单位附属绿地等,退化绿地则包括自然退化和人为退化等.计划新增绿地和退化绿地分别用计划新增绿地比例和退化绿地比例来表示,考虑到数据获取的难易性和分析问题时关键因素的代表性,本文仅选择计划新增公共绿地比例、计划新增生产绿地比例、计划新增单位附属绿地比例三部分计算计划新增绿地比例.绿化率分析模型如图1所示.
绿化率分析模型的数学表达式为
Z=INTEG(Z1-T,C);
Z1=Z·B;
B=B1+B2+B3;
T=Z·T1;
B1=A FUNCTION OF(Time);
B2=A FUNCTION OF(Time);
B3=A FUNCTION OF(Time);
L=S/(S1·G);
S1=B-T1;
S=Z1-T;
T1=AFUNCTION OF(Time);
C=C1(C1为常数);
G=C2(C2为常数).
式中,Z表示总绿地面积;Z1表示计划新增绿地面积;T表示退化面积;C表示初始化总绿地面积;B表示计划新增绿化比例;B1表示计划新增公共绿地比例;B2表示计划新增单位附属绿地比例;B3表示计划新增生产绿地比例;T1表示退化比例;L表示绿化率;S表示实际新增绿地面积;S1表示实际绿化比例;G表示总面积.

图1 绿化率分析模型Fig.1 Greening rate analysis model
1.2 交通便宜度分析模型
公交车分担率、出租车分担率、小汽车分担率都对交通便宜度有一定的影响,公交车、小汽车、出租车分担率受到出行总量和公交车、小汽车、出租车出行量的影响,而出行量由人均出行次数和总人口数量决定,公交车、小汽车、出租车出行量由公交车、小汽车、出租车数量和公交车、小汽车、出租车出行频率决定;总人口数量是出生人口和死亡人口的差值,出生人口和死亡人口分别用出生率和死亡率表示.交通便宜度分析模型如图2所示.
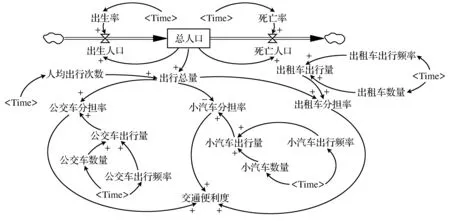
图2 交通便宜度分析模型Fig.2 Traffic convenience degree analysis model
交通便宜度分析模型的数学表达式为:
式中,T表示总人口;Tr表示出生人口;Ts表示死亡人口;T0表示总人口的初始值;Trv表示出生率;Tsv表示死亡率;Tp表示人均出行次数;Tbv表示公交车分担率;Tz表示出行总量;Tb表示公交车出行量;Tbf表示公交车出行频率;Tbm表示公交车数量;Tcv表示小汽车分担率;Tc表示小汽车出行量;Tcf表示小汽车出行频率;Tcm表示小汽车数量;Ttv表示出租车分担率;Tt表示出租车出行量;Ttf表示出租车出行频率;Ttm表示出租车数量;Tc表示交通便宜度.
1.3 居民素质水平分析模型
初等教育就业人数、中等教育就业人数、高等教育就业人数对居民素质水平都有影响.不同等级的就业人数受到不同等级毕业人数和就业率的影响,就业率是随时间变化的量,而不同等级毕业人数是由相应的毕业率和在校人数决定的,在校人数又受到入学率和升学率的影响.居民素质水平分析模型如图3所示.
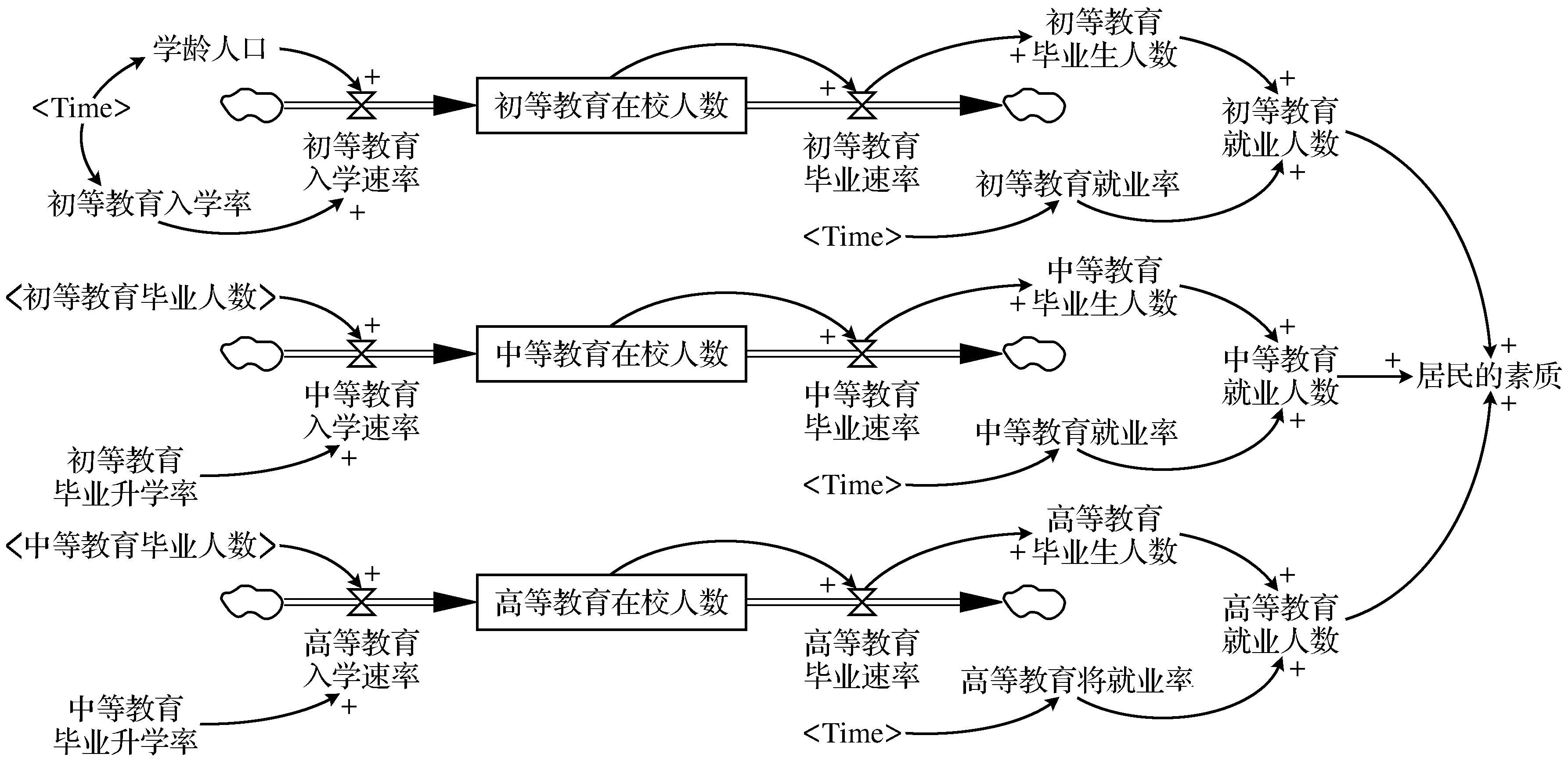
图3 居民素质水平分析模型Fig.3 Residents’ quality level analysis model
居民素质水平分析模型的数学表达式为
式中,P表示初等教育在校人数;Pr表示初等教育入学速率;Pb表示初等教育毕业速率;P1表示初等教育的在校人数的初始值;Pv表示初等教育入学率;Px表示学龄人口;Pbs表示初等教育毕业人数;Pj表示初等教育就业人数;Pjv表示初等教育就业率;Ps表示初等教育毕业升学率;M表示中等教育在校人数;Mr表示中等教育入学速率;Mb表示中等教育毕业速率;M1表示中等教育在校人数的初始化值;Mbs表示中等教育毕业人数;Mjv表示中等教育就业率;Mj表示中等教育就业人数;Ms表示中等教育毕业升学率;G表示高等教育在校人数;Gr表示高等教育入学速率;Gb表示高等教育毕业速率;G1表示高等教育在校人数的初始值;Gjv表示高等教育就业率;Gbs表示高等教育毕业生人数;Gj表示高等教育就业人数;U表示居民的素质水平.
1.4 医疗技术水平分析模型
医疗技术水平受到医院固定资产、医院高技术人才比例和医院数量的影响,医院固定资产是医院固定资产增量与医院资产折旧的差值;医院高技术人才比例和医院总收入存在一定的关系,医院总收入由政府对医院的投入和医院业务收益组成,医院的业务收益又可划分为医院门诊收益和医院住院收益,同时医院的总收入还对医院固定资产增量有影响;医院数量短期内可以视为常量.医疗技术水平分析模型如图4所示.
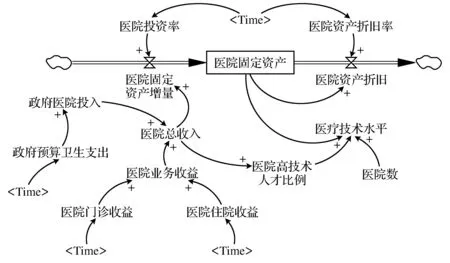
图4 医疗技术水平分析模型Fig.4 Medical technology level analysis model
医疗技术水平分析模型的数学表达式为:
式中,H表示医院固定资产;Hz表示医院固定资产增量;Hj表示医院资产折旧;H1表示医院固定资产的初始值;Hv表示医院资产折旧率;Ht表示医院投资率;Hs表示医院总收入;Hr表示政府医院投入;Hy表示医院业务收益;Hzy表示医院住院收益;Hmy表示医院门诊收益;Hw表示政府预算卫生支出;Hg表示医院高技术人才比例;He表示医疗技术水平;H0表示医院数.
1.5 商业服务质量分析模型
商业服务质量主要受到商品价格不合理比例、员工高素质比例以及便民设施投入比例的影响,商品价格不合格比例是由商品标准平均价格和商品平均价格决定的,商品平均价格受商品总价格和商品总数量的影响;员工高素质比例与商业总收入存在一定的关系,商业总收入又是由商业利润和商业损失组成的;便民设施投入比例则是由商业投入和政府投入决定的,其中商业投入与商业收入存在一定的关系.商业服务质量分析模型如图5所示.
商业服务质量分析模型的数学表达式为:
Bz=INTEG(B1-Be,B0);
B1=Bp·Bx;
B0=C1(C1为常数);
Bx=A FUNCTION OF(Time);
Bp=Bzp/Bzm;
Bpb=C2(C2为常数);
Bzp=A FUNCTION OF(Time);
Bzm=A FUNCTION OF(Time);
Be=Bz·Bev;
Bn=(Bp-Bpb)/Bpb;
Bev=A FUNCTION OF(Time);
Br=A FUNCTION OF(Bz);
Bc=A FUNCTION OF(Br,Bg);
Bg=A FUNCTION OF(Time);
Bb=A FUNCTION OF(Bc,Bs,Bn);
Bs=A FUNCTION OF(Bz).
式中,Bz表示商业总收入;B1表示商业利润;Be表示商业损失;B0表示商业总收入的初始值;Bp表示商品平均价格;Bx表示商品总销售量;Bzp表示商品总价格;Bzm表示商品总数量;Bev表示损失率;Br表示商业投入;Bc表示便民设施投入比例;Bg表示政府投入;Bn表示商品价格不合理比例;Bpb表示商品标准平均价格;Bs表示员工高素质比例;Bb表示商业服务质量.

图5 商业服务质量分析模型Fig.5 Business service quality analysis model
2 模型检验
模型建立完成之后,必须通过仿真实验对模型进行检验,以保证模型的正确性、可靠性和实用性.模型检验主要由模型的一致性检验和有效性检验两部分组成[5-6].模型的一致性检验主要包括对模型结构的合理性、模型量纲的一致性、模型界限的恰当性进行检验,以及对模型是否反映真实实际情况进行检验等,这一部分检验已经在模型建立过程中给予了较为充分的考虑,并且在模型仿真过程中又对其进行了不断的修改和完善,直至达到模型一致性要求为止.模型的有效性检验主要通过对历史数据的仿真来判定,如果一个模型的模拟数据与历史数据差距较大,则这个模型是不可靠的.
结合沈阳市铁西区2002—2010年统计年鉴中提供的有效数据[7], 利用参数估计方法对本文所构建模型中的参数进行赋值, 根据输入的数据和方程关系可得出一组计算结果. 以绿化率分析模型为例, 借鉴沈阳市铁西区统计年鉴中提供的有效数据, 将2002年的数据作为初始数据, 利用真实数据与估计数据对绿化率分析模型中公式的变量,以及方程进行赋值,计算结果如式(1)所示.
(1)
采用相同的方法,通过对交通便宜度分析模型、医疗技术水平分析模型、居民素质水平分析模型和商业服务质量分析模型中的变量及方程进行赋值,即可得到相应的仿真结果.各个模型的主要变量的计算结果与真实实际数据之间拟合情况如表1所示.

表1 仿真结果误差分析Table 1 Error analysis of simulation results
续表1
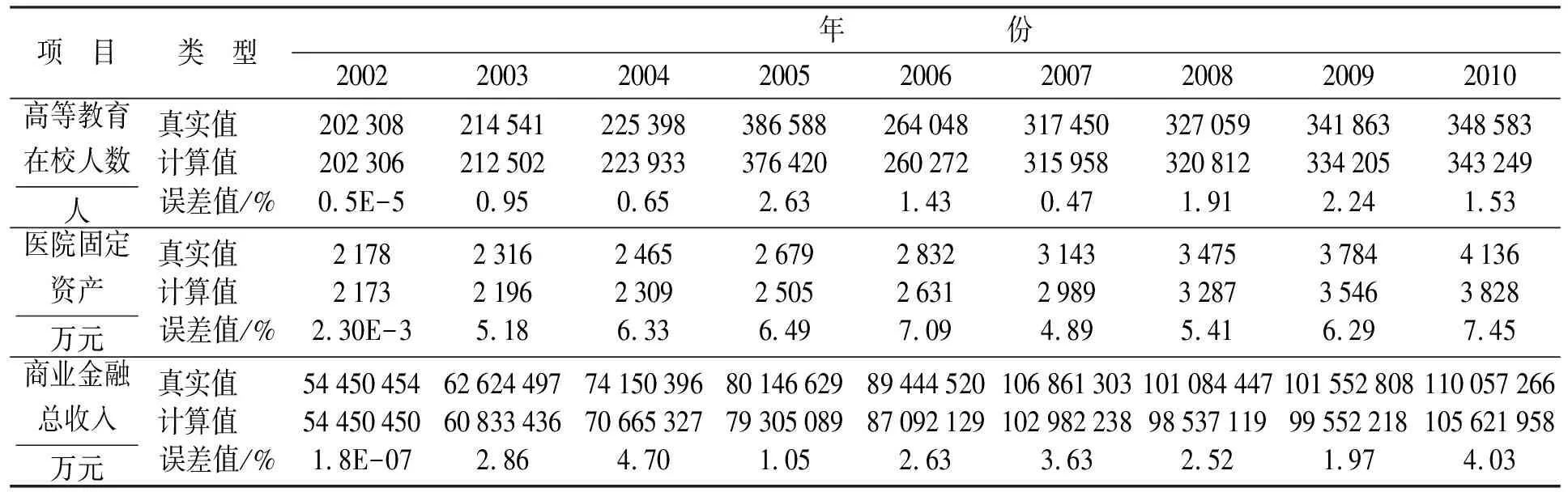
项 目类 型年 份200220032004200520062007200820092010高等教育在校人数人真实值 202308214541225398386588264048317450327059341863348583计算值 202306212502223933376420260272315958320812334205343249误差值/%0.5E-50.950.652.631.430.471.912.241.53医院固定资产万元真实值 217823162465267928323143347537844136计算值 217321962309250526312989328735463828误差值/%2.30E-35.186.336.497.094.895.416.297.45商业金融总收入万元真实值 5445045462624497741503968014662989444520106861303101084447101552808110057266计算值 54450450608334367066532779305089870921291029822389853711999552218105621958误差值/%1.8E-072.864.701.052.633.632.521.974.03
系统动力学的观点认为,模拟结果的误差在10%以内均认为是合理的.从表1中可以看出真实数据与模拟数据间的误差都在误差允许的范围之内,表明模拟数据与真实数据的拟合程度较好,模型具有一定的可信度,可以反映真实实际情况.
3 结 论
城区环境问题是一个涉及面广、关系错综复杂的社会系统问题,城区环境是否宜居受诸多因素影响,其中包括对城区宜居环境质量影响较大的关键影响因素.本文以系统动力学理论为依据,综合利用系统分析方法,针对绿化率、交通便宜度、居民素质水平、医疗技术水平和商业服务质量等关键影响因素构建系统动力学模型,并利用参数估计方法对所构建的模型进行一致性和有效性检验,为确定城区宜居环境仿真算法和开发仿真系统做准备.
参考文献:
[1]吴良镛. 人居环境科学导论[M]. 北京:中国建筑工业出版社, 2001:1-5.
(Wu Liangyong. Introduction to Science of Human Settlements[M]. Beijing: China Architecture & Building Press, 2001:1-5.)
[2]王琳. 宜居城市理论与影响因素研究[D]. 杭州: 浙江大学, 2007:20-25.
(Wang Lin. Study of Livable City Theory and Its Influence Factors[D]. Hangzhou: Zhejiang University, 2007:20-25.)
[3]李丽萍,吴祥裕. 宜居城市评价指标体系研究[J]. 中共济南市委党校学报, 2007(1):16-21.
(Li Liping, Wu Xiangyu. Research on the Evaluation Index System of Livable City[J]. Journal of the Party School of CPC Jinan Municipal Committee, 2007(1):16-21.)
[4]陆仕祥,覃青作. 宜居城市理论研究综述[J]. 北京城市学院学报, 2012(1):13-16.
(Lu Shixiang, Qin Qingzuo. Research on Livable City Theory[J]. Journal of Beijing City University, 2012(1):13-16.)
[5]王其藩. 系统动力学[M]. 上海: 上海财经大学出版社, 2009:100-120.
(Wang Qifan. System Dynamics[M]. Shanghai: Shanghai University of Finance and Economics Press, 2009:100-120.)
[6]刘兴堂. 复杂系统建模理论、方法与技术[M]. 北京: 科学出版社, 2011:110-160.
(Liu Xingtang. The Complex System Modeling Theory, Method and Technology[M]. Beijing: Science Press, 2011:110-160.)
[7]沈阳市铁西区统计局. 铁西区统计年鉴[R]. 2001—2012:170-300.
(Statistical Bureau of Tiexi District of Shenyang. Tiexi Statistical Yearbook[R]. 2001-2012:170-300.)
