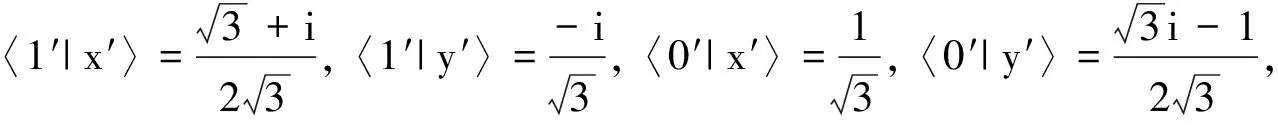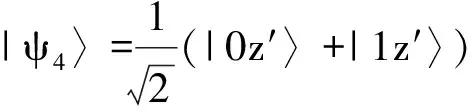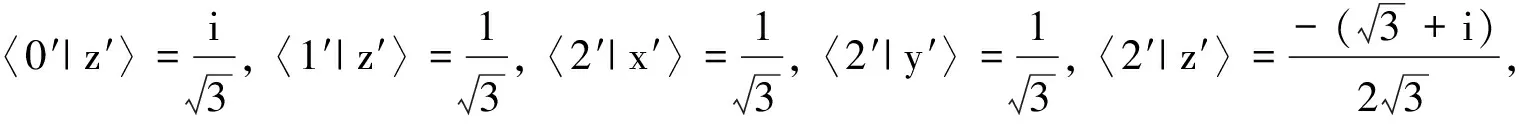2×3量子系统中互不偏的不可扩展最大纠缠基
2014-03-25李玮林平郑鸿楠秦川棋杨强陶元红
李玮, 林平, 郑鸿楠, 秦川棋, 杨强, 陶元红
( 延边大学理学院 数学系, 吉林 延吉 133002 )
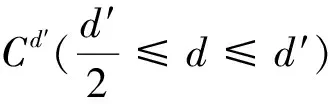
本文主要讨论了2×3量子系统中彼此互不偏的不可扩展的最大纠缠基.通过变换C3空间的基底,构造了彼此无偏的两组均由4个彼此规范正交的最大纠缠态构成的2×3量子系统中不可扩展的最大纠缠基,并在保证无偏的前提下,将这两组不可扩展的最大纠缠基进行了完备化.
1 C2⊗C3中不可扩展的最大纠缠基
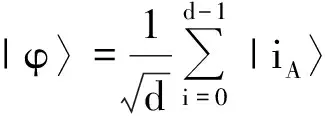
定义2[4]由态{|φi〉∈Cd⊗Cd′:i=1,2,…,n,n 1) |φi〉,i=1,2,…,n均为最大纠缠态; 2) 〈φi|φj〉=δij; 3) 若对任意i=1,2,…,n, 均有〈φi|φ〉=0, 则φ必不是最大纠缠的. 首先构造2×3量子系统中的不可扩展的最大纠缠基.考虑C2⊗C3中如下4个彼此规范正交的最大纠缠态: (1) 其中{|0〉,|1〉},{|0′〉,|1′〉,|2′〉}分别为C2和C3中的标准正交基. 定理1(1)式中的4个最大纠缠态构成了C2⊗C3中一组不可扩展的最大纠缠基. 证明显然(1)式中的每个态都是C2⊗C3中的最大纠缠态,且彼此规范正交. 即 (2) (3) (4) (5) 显然,(2)—(5)式可写成 (6) 即为齐次方程组 Av=0. (7) 综上,(1)式中的4个向量构成了C2⊗C3中的一组不可扩展的最大纠缠基. 首先在C3中选取与{|0′〉,|1′〉,|2′〉}不同的另一个标准正交基(此组基与文献[5]中的完全不同): (8) 然后利用定理1,构造C2⊗C3中的第2组不可扩展的最大纠缠基 (9) 容易证得,(1)式和(9)式这两组不可扩展的最大纠缠基是互不偏的,即 (10) 事实上,由于 (11) (12) 为了证明这两组基是互不偏的,只需证明如下两组等式即可: (13) 事实上,由于 综上可知,(11)式和(12)式构成了2×3量子系统中一对完备的互不偏的不可扩展的最大纠缠基. 参考文献: [1] Nielsen M A, Chuang I L. Quantum Computation and Quantum Information[M]. London: Cambridge University Press, 2000:98-106. [2] Bennett C H, DiVincenzo D P, Fuchs C A, et al. Quantum nonlocality without entanglement[J]. Physical Review A, 1999,59:1070-1091. [3] DiVincenzo D P, Mor T, Shor P W, et al. Unextendible product bases, uncompletable product bases and bound entanglement[J]. Communication in Math Phys, 2003,238:379-410. [4] Bravyi S, Smolin J A. Unextendible maximally entangled bases[J]. Phys Rev A, 2011,84:042306. [5] Chen Bin, Fei Shaoming. Unextendible maximally entangled bases and mutually unbiased bases[J]. Phys Rev A, 2013,88:034301. [6] Wootters W K, Fields B D. Optimal state-determination by mutually unbiased measurements[J]. Ann Phys, 1989,191:363-381. [7] Englert B G, Aharonov Y. The mean king’s problem: prime degrees of freedom[J]. Phys Lett A, 2001,1:284. [8] Fernandez-Perez A, Klimov A B, Saavedra C. Quantum process reconstruction based on mutually unbiased basis[J]. Phys Rev A, 2011,83:052332. [9] Adamson R B A, Steinberg A M. Improving quantum state estimation with mutually unbiased bases[J]. Phys Rev Lett, 2010,105:030406. [10] Yu L C, Lin F, Huang C Y. Quantum secret sharing with multilevel mutually (un)biased bases[J]. Phys Rev A, 2008,78:012344. [11] Cerf N J, Bourennane M, Karlsson A, et al. Security of quantum key distribution using d-level systems[J]. Phys Rev Lett, 2002,88:127902.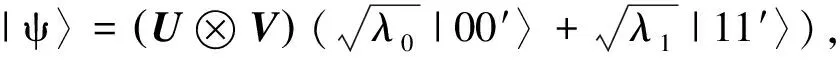
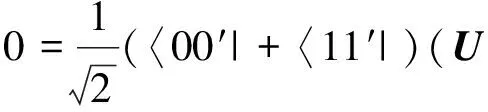
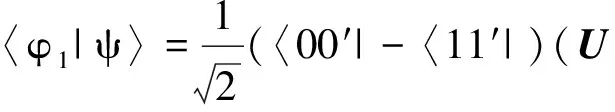
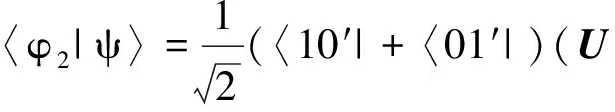
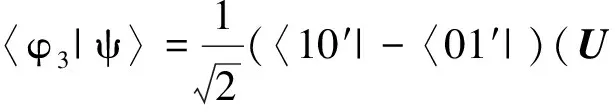
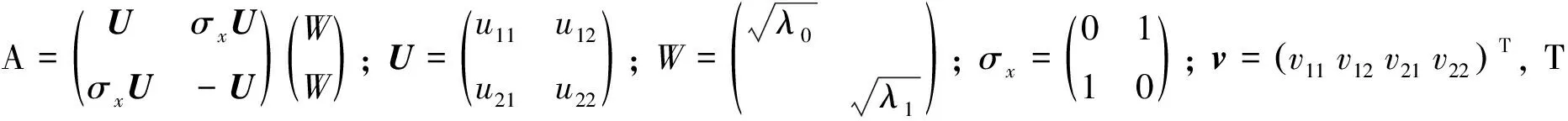
2 2×3量子系统中互不偏的不可扩展最大纠缠基