具有预警功能和可修复储备部件的人-机系统

韩筱爽， 方明

( 1.延边大学科学技术学院, 吉林 延吉 133002； 2.延边大学理学院 数学系, 吉林 延吉 133002 )

0 引言

所谓预警[1-2]是指在灾害或灾难以及其他需要提防的危险发生之前，根据以往总结的规律或观测得到的可能性前兆，使系统发出紧急信号报告危险情况，以避免灾害在不知情或准备不足的情况下发生，从而最大限度地降低危害所造成的损失的行为.预警系统是指具备上述功能的系统.文献[3-7]中作者讨论了一类具有2个运行部件和1个储备部件、故障修复时间服从一般分布的人-机系统模型，运用泛函分析中Banach空间上的线性算子半群理论,先后证明了系统解的存在唯一性、半离散化、渐进稳定性、指数稳定性和系统的谱特征，并分析了其可靠性.

本文在上述模型上，增加一个新的预警状态，使之成为具有可修复储备部件和预警功能的人-机系统模型，使得系统的初值条件属于定义域，这样原来利用Banach空间上线性算子半群方法求得的弱解变成了强解.在此基础上,对系统的稳定性、预警与非预警系统(相对于本文的系统状态，原来所研究的即为非预警系统)的稳态可用度进行了研究，最后通过数值计算表明，当风险失效率取特定值时，预警与非预警系统稳态可用度的相对误差趋于0.这样，在生产生活中，可根据风险系数的实际意义，做出合理的风险预测，建立相应预警系统模式，从而最大限度减少各种危害造成的损失.

1 模型描述

系统的状态转换流程如图1所示,其中:i=0表示2个运行部件和1个储备部件均处于完好状态;i=1表示1个运行部件因硬件错误而故障, 1个储备部件立即补充运行;i=2表示系统仅有1个部件正常运行而无储备部件;i=3表示系统由于硬件错误而处于故障状态;i=4表示系统由于通常错误而处于故障状态;i=5表示系统由于临界人为错误而处于故障状态;i=c表示系统由于通常错误而处于故障状态,但系统仍能继续运行(预警状态).该模型可用如下积分-微分方程描述:

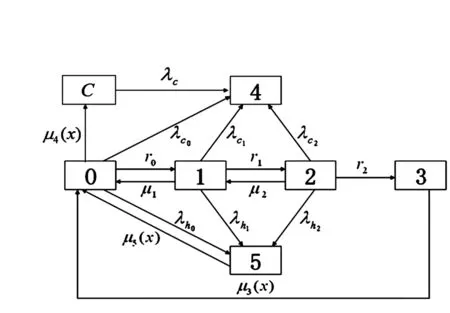
图1 系统工作流程

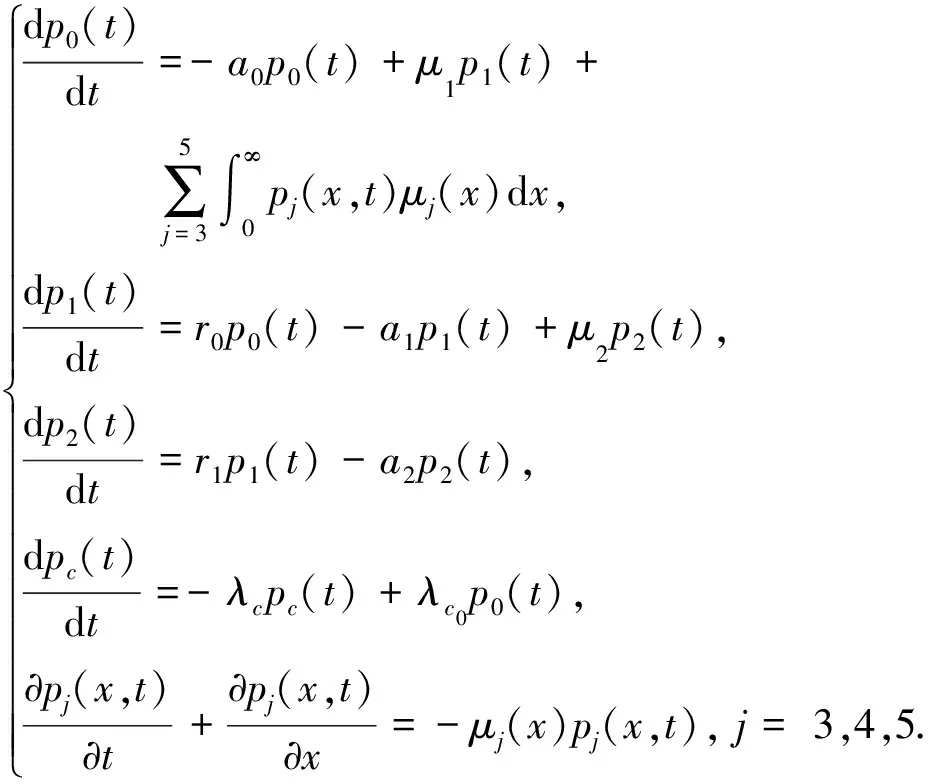
(1)

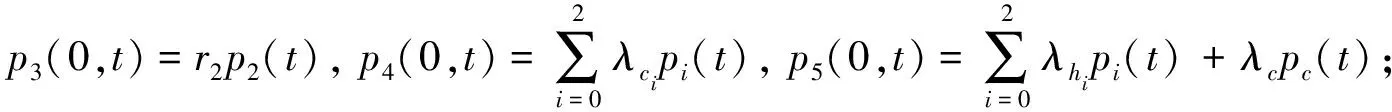
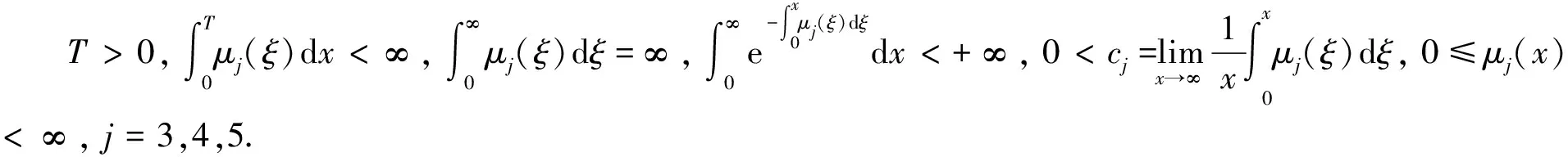
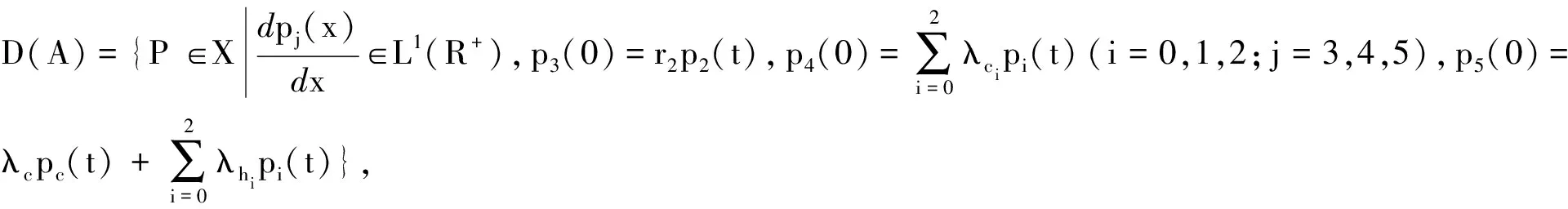
(2)

其中p(t)=(p0(t),p1(t),p2(t),pc(t),p3(x,t),p4(x,t),p5(x,t)).

2 系统解的性质

根据文献[4-7]中的证明方法可得如下结论:

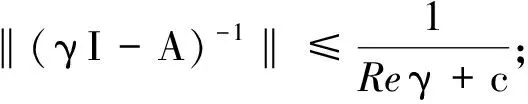
定理2柯西问题(2)具有唯一非负时间依赖弱解P(t)=T(t)P(0),t∈[0,∞).

推论1设A如前定义,正数c如前假设,则算子A生成压缩半群S(t)是指数衰减的,即对任意c>ω>0,‖S(t)‖≤e-ω t,t≥0.

定理3设A如前定义,正数c如前假设,则A+E生成的压缩半群T(t)具有以下性质:

1)当{γ∈C:Reγ>0}时,γ∈σ(A+E)⟺D(γ)=0;

2)设γ0=0, 对任意的γk={γ∈C|Reγ+c>0,D(γ)=0},γk≠γ0, 其中γk按照实部递减排序,即Reγk+1≤Reγk,k=1,2,…,N, 则γ0=0是A+E的严格占优本征值;

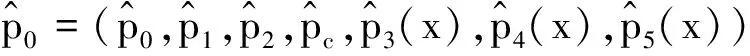
上述结果表明,在一定的条件下系统的动态解以指数形式收敛于系统的稳态解.

3 系统解的稳态可用度

首先假设风险失效率λc=αλ, 当α→∞时,即系统发出预警提示后不去检查或修理,使其继续工作,即预警功能未能起到预警作用,那么此时的系统模型回归到非预警系统,由文献[5]求得非预警系统的稳态可用度为

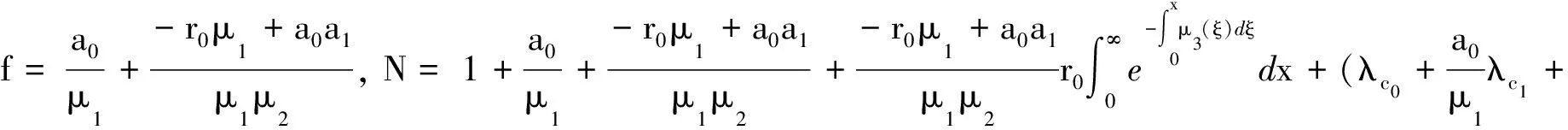
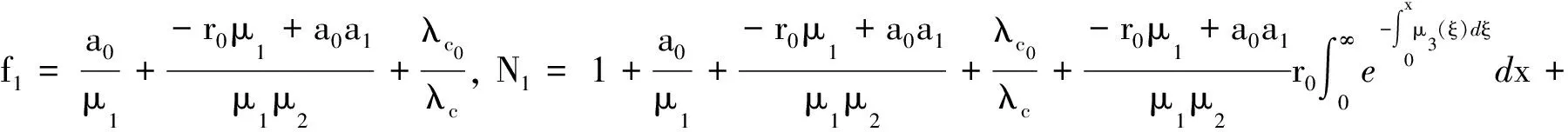
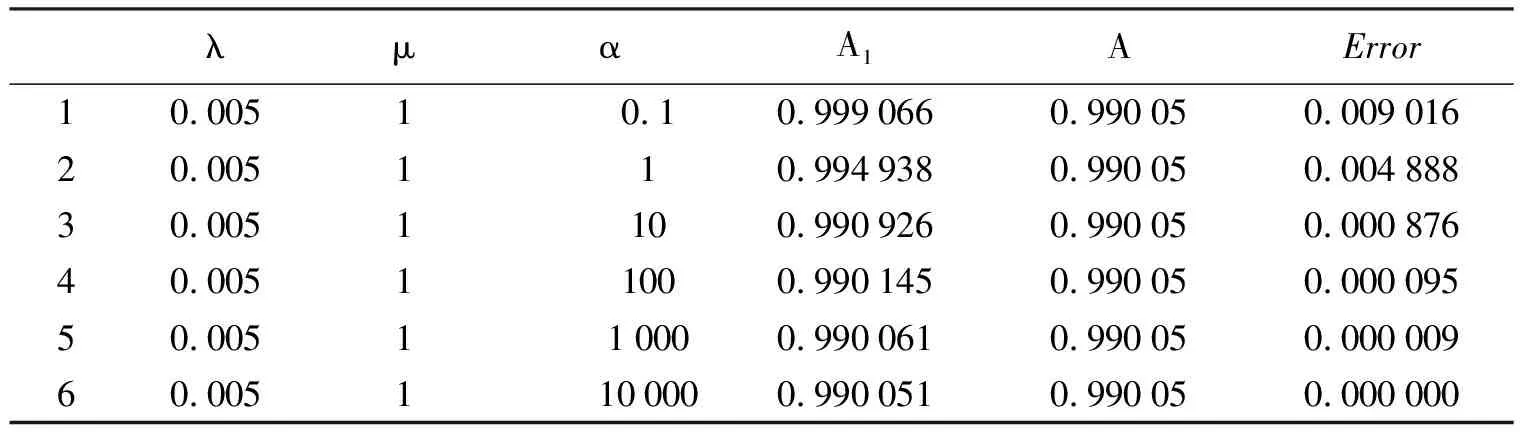
表1 预警与非预警系统相对误差变化情况(μ=1)

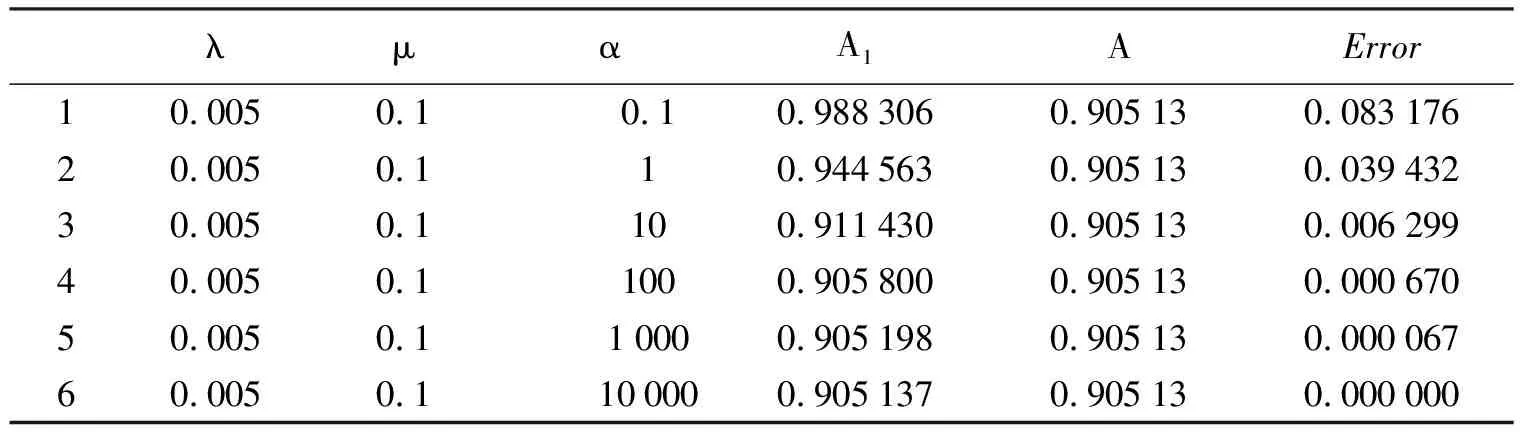
表2 预警与非预警系统相对误差变化情况(μ=0.1)

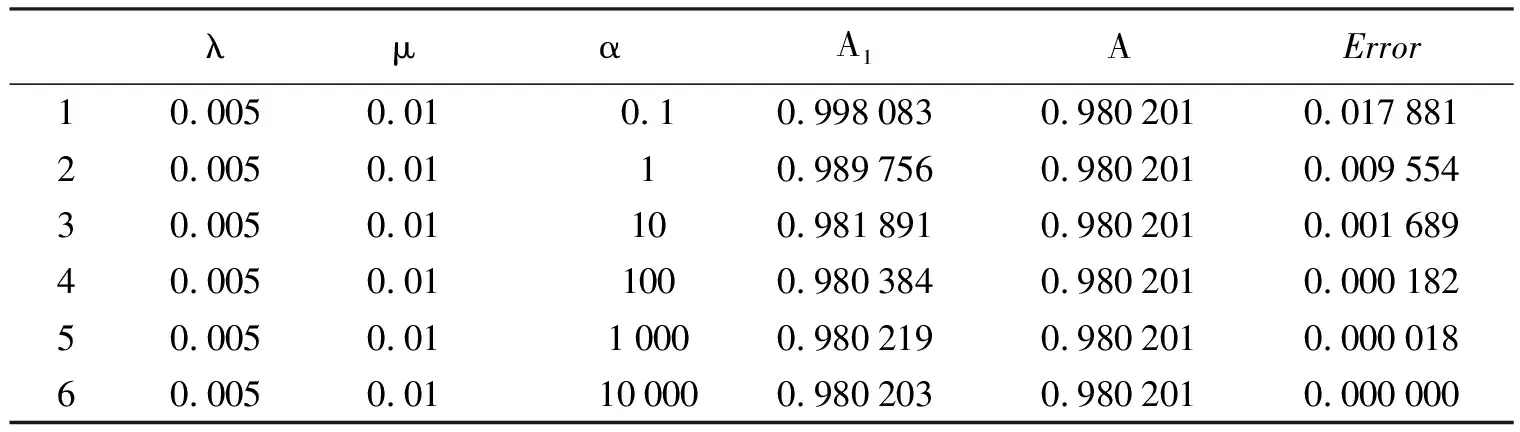
表3 预警与非预警系统相对误差变化情况(μ=0.01)

参考文献：

[1] 曹晋华,程侃.可靠性数学引论[M].北京:科学出版社,1986:182-244.

[2] 高超,朱广田.具有预警功能的可修复系统[J].应用泛函分析学报,2011，13(1):19-29.

[3] Nianfu Yang, Dhillon BS. Availability analysis of a repairable standby human-machine system[J]. Microelectron Reliab, 1995,35:1401-1413.

[4] 方明,韩筱爽.一类具有可修复储备部件的人-机系统的解的存在唯一性[J].延边大学学报:自然科学版,2008,34(1):14-17.

[5] 方明,韩筱爽.一类具有可修复储备部件的人-机系统的解的谱特性[J].延边大学学报:自然科学版,2009,35(4):305-308.

[6] 姜英秀,韩筱爽.一类具有可修复储备部件的人-机系统解的指数稳定性[J].延边大学学报:自然科学版,2012,38(2):108-111.

[7] 韩筱爽,程龙.一类具有可修复储备部件的人-机系统的可靠性分析[J].延边大学学报:自然科学版,2013,39(1):9-13.