复合材料布带缠绕纠偏模糊控制技术研究

何晓东, 史耀耀, 秦现生

(西北工业大学 机电学院, 陕西 西安 710072)

碳纤维以及酚醛树脂布带缠绕技术主要应用在航空发动机喷管绝热层、火箭壳体等部件的制造等方面[1-2]。缠绕过程中由于导辊的安装误差、布带速度及张力的波动等因素影响,布带会发生横向偏移,即布带跑偏现象。布带跑偏将引起缠绕过程中布带产生折皱、翻边甚至破损,进而影响缠绕制品性能[3],因此,对布带跑偏现象进行纠偏是布带缠绕成型控制技术的关键之一。

文献[4]提出了一种基于CCD传感器的模糊PID布带纠偏控制方法,纠偏采用单辊,纠偏效果存在明显的积分效应;文献[5]提出了一种带前馈的印纺机械纠偏控制方法,研究主要针对恒张力、恒线速收放卷系统的纠偏;文献[6]采用电液伺服系统对带钢进行纠偏控制,液压系统存在油污染隐患,不适于复合材料缠绕工艺。复合材料布带缠绕成型过程,不同工艺要求,其使用的预浸胶布带材料、缠绕张力及缠绕速度均不同,其纠偏系统特性也将随之变化,相比较于此,印纺、带钢等纠偏控制有一定局限性。而文献[4]中采用的纠偏控制方法使用单辊纠偏结构,积分效应明显,纠偏易出现超调,针对于此,提出一种基于平行双辊结构的布带模糊纠偏控制系统,并对纠偏性能进行实验研究。

1 复合材料布带缠绕传动特性分析

复合材料布带缠绕工艺如图1所示,在缠绕温度、缠绕压力及缠绕张力的共同作用下将复合材料预浸胶布带按一定缠绕速度缠绕于模具上。

图1 复合材料布带缠绕工艺

复合材料布带缠绕过程中,带盘边缘误差、导辊安装误差等现象造成传动中的布带产生横向偏移是布带跑偏的主要原因。因此布带在缠绕导辊系间传动的运动特性分析是纠偏控制研究的关键。

图2所示为缠绕布带在平行双导辊间的运动。缠绕布带的运动可由基于弹性曲率原理的动力学方程表示[7-8],根据其理论,带在辊系间的横向及纵向运动中可以用一个四阶偏微分方程表示,如公式(1)所述。

图2 导辊间布带横向运动

(1)

式中：y为带的横向运动分量,x为带的纵向位移分量,K2=T/EI,T为缠绕张力,E为缠绕布带弹性模量,I为缠绕布带摆动时的转动惯量。公式(1)的通解即为布带缠绕过程中横向运动方程,如下所示。

y=C1sinh(Kx)+C2cosh(Kx)+C3x+C4

(2)

通解中系数C1、C2、C3、C4可由图2中布带传动时的边界条件得到,从布带的横向位移及布带在2个导辊的切入角可得到的4个边界条件为:

式中:y0为输入辊处布带横向位移,yL为输出辊处布带横向位移,θ0为输入辊处布带与x轴夹角,θL为输出辊处布带与x轴夹角。将上述边界条件代入公式(1),可得:

复合材料布带缠绕过程中,要求预浸胶布带不折皱始终保持平直,即θ0≈θL,基于此,将系数C1、C2、C3、C4代入公式(2)的二阶偏导,可得到缠绕过程预浸胶布带传动特性,其结果如公式(3)所示。

(3)

式中:

2 布带纠偏控制模型研究

图3所示为复合材料布带缠绕纠偏机构,主要由布带位置检测传感器、双平行导辊纠偏架、传感器支架、电机等部分。双平行导辊纠偏架由电机驱动实现绕转动支点摆动,进而带动纠偏架上的布带平移,实现布带纠偏,此平移运动近似正比于纠偏架摆动角度,相比于单辊纠偏响应速度更快。

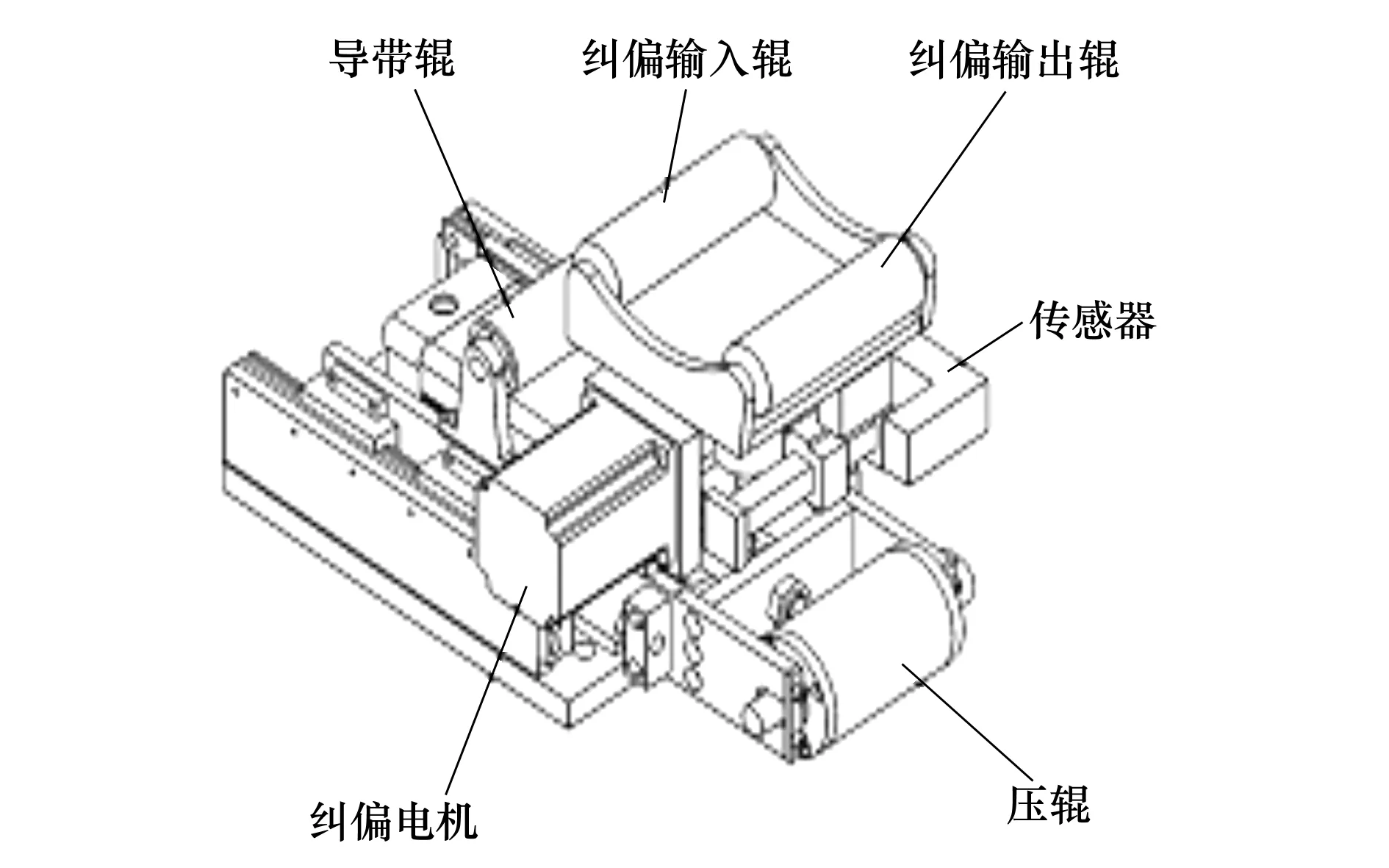
图3 双平行导辊纠偏系统

布带缠绕纠偏机构进行纠偏时,其运动可分解为三部分:①纠偏输入辊与导带辊间布带传动时产生的横向偏移运动;②纠偏输入、输出辊间布带传动时产生的横向偏移运动;③纠偏机构动作时产生的带横向平移。

2.1 纠偏机构输入端布带横向运动特性

纠偏动作产生后,由于纠偏架的偏摆,纠偏输入辊与导带辊产生了相对运动。导带辊系发生相对位置变化时,布带横向运动的速度与加速度方程可由公式(4)、(5)表示[9]。

(4)

(5)

式中:δ为纠偏机构的摆动角,y为布带的横向位移,x为布带的纵向位移,z为导辊间的相对横向移动,v为布带的缠绕速度。

图4 纠偏辊摆动作用分析

如图4所示,纠偏动作执行后,纠偏输入辊产生纠偏角δ,且相对导带辊1出现了横向移动z0,传动中的带产生了偏移。根据公式(3)及公式(5),可得预浸胶布带在导带辊1与输入辊间横向运动的加速度方程,如公式(6)所示。

(6)

式中:yd为导带辊处布带横向位移;y0为纠偏输入辊处布带的横向位移;θ0为纠偏输入辊处带与输入辊的偏移角度。根据图4所示,纠偏输入辊的水平移动量z0与摆动角度δ的关系为:

z0=L1δ

(7)

由公式(4)可得:

(8)

将公式(7)、(8)代入公式(6)中,得到缠绕导带辊1与纠偏输入辊间带横向运动特征,如公式(9)所示。

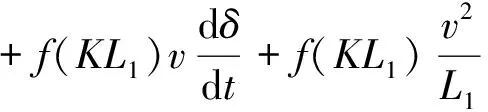
(9)

如上所述,缠绕导带辊为双输入单输出系统,输入为纠偏机构的偏转,以及布带在其他辊系的扰动,输出为布带在导带输入辊处的偏移。将(9)式转换为状态空间方程,如公式(10)所示

(10)

2.2 纠偏机构中布带横向运动特性

纠偏机构采用双平行辊结构,纠偏动作执行过程如图5所示。

图5 布带纠偏运动示意

由纠偏机构结构可知,辊系间平行且不存在相对运动,即δ=0,d2z/dt2=dz/dt=0,因此公式(4)、(5)可简化为公式(11)、(12)。

(11)

(12)

式中：L为双平行纠偏辊之间距离,将公式(3)、(11)代入公式(12)中可得公式(13)。

(13)

将公式(13)转换为状态空间方程,获得缠绕纠偏机构的带运动特性,即缠绕纠偏机构带输入位置与带输出位置件间的传递函数,如公式(14)所示。

(14)

2.3 纠偏作用产生的布带横向平移特性

纠偏作用产生后,纠偏机构带动其中的预浸胶布带进行整体移动产生纠偏效果。当纠偏机构绕旋转轴摆动时,布带产生的横向平移量如公式(15)所述:

y2=(L-L1)δ

(15)

如前述分析,缠绕布带纠偏作用由缠绕导带辊1与纠偏机构输入辊间的带横向运动,纠偏机构双平行辊间的带运动以及纠偏机构产生的水平移动作用组成,根据公式(10)、(13)、(14),建立缠绕带纠偏运动的状态空间方程,如公式(16)所示。

(16)

纠偏运动模型中,输入量为纠偏机构摆角δ及带传动过程的干扰量yd,输出量为带纠偏位移y3。

3 模糊纠偏控制策略研究

复合材料布带缠绕过程中,针对不同缠绕工艺要求,缠绕张力及缠绕速度均不同,通常复合材料带缠绕张力作用范围为100～500 N,缠绕速度范围为50～1 000 mm/s。

针对这种时变的缠绕纠偏系统,采用传统控制方法,如PID控制等,其控制效果难以令人满意。为了获得更好的缠绕质量,提出模糊纠偏控制方法。

定义布带偏移变量Y的语义变量为{NB,NM,NS,G,PS,PM,PB},分别对应布带偏移量的负很大、负大、负一般、合适、正一般、正大、正很大;定义布带偏移速度的语义变量为{NB,NM,NS,ZE,PS,PM,PB},对应负很大、负大、负一般、合适、正一般、正大、正很大;定义纠偏输出U的语义变量为{NB,NM,NS,Z,PS,PM,PB},分别对应负快、负中速、负慢、零、正慢、正中速、正快。

缠绕过程中,布带偏移量大小是一个根据缠绕制品质量定义的模糊集合。使用XP-1000型缠绕机进行缠绕实验,通过红外传感器EC-2323A检测缠绕布带偏移量,根据缠绕实验定义布带偏移量Y大小的隶属度,取布带偏移量分别为0、±0.5、±1、±2、±3、±4、±5、±6、±7、±8、±9,与之对应的缠绕质量为好、好、一般、一般、差、差、很差、很差、破损、破损、破损,基于此实验结果,设计布带偏移量的隶属函数如图6所示。

图7所示为布带偏移量速度的隶属函数,布带偏移量速度大小的模糊关系采用均布的三角隶属函数[9]。

纠偏电机的额定输入为5 V,电机转速与输入近似线性,基于此,纠偏输出的隶属函数采用均布的三角隶属函数,如图8所示。

图6 布带偏移量隶属函数 图7 布带偏移速度隶属函数 图8 纠偏输出隶属函数

选取3组不同的缠绕张力、缠绕速度进行仿真。布带缠绕纠偏的模糊控制及PID控制的仿真结果分别如图10、图11所示。

图9 模糊纠偏仿真结果

图10 PID纠偏仿真结果

仿真结果显示,当张力、缠绕速度变化时,采用模糊控制器的纠偏系统仍然能够保持很好的控制效果,而采用PID控制器时,控制效果受系统变化影响较大,当缠绕张力为400 N、缠绕速度为800 mm/s时,纠偏出现了较大波动。

4 纠偏控制实验

基于上述分析,选用XP-1000数控缠绕机,以85 mm宽酚醛树脂基玻璃纤维布带为实验对象,采用边缘检测方式进行布带缠绕纠偏实验。

表1 纠偏控制实验结果

采用模糊控制与PID控制,在3组不同缠绕张力、缠绕速度组合下各进行3次纠偏实验,每次实验持续2 min,取缠绕过程中布带的最大跑偏量,实验结果如表1所示。

实验数据表明,缠绕张力为100 N、缠绕速度为100 mm/s时,PID纠偏控制与模糊纠偏控制的控制偏差相差不大,随着缠绕张力及缠绕速度的增大,PID纠偏的控制偏差明显增大,增幅最大超过4 mm,而模糊纠偏的控制偏差仅增加了0.2 mm,采用模糊纠偏控制,其纠偏精度不低于0.6 mm,满足布带缠绕工艺要求。图11所示为张力为400 N、缠绕速度为800 mm/s时的缠绕纠偏实验。如图11所示,使用PID纠偏控制时,带纠偏经过较大震荡后才趋于稳定,使用模糊纠偏控制时纠偏控制偏差小,缠绕制品边缘平整。

图11 布带缠绕纠偏实验

5 结 论

1) 在分析了缠绕成型过程中布带传动特性的基础上,根据缠绕纠偏机构特点,分别对输入辊、纠偏导带辊及纠偏作用进行布带横向运动进行分析,并最终得到布带纠偏运动的模型。

2) 基于布带纠偏运动模型中存在时变参数的特点,提出了模糊纠偏控制系统,在缠绕实验的基础上建立了模糊纠偏控制的隶属函数,在simulink环境中建立的模糊纠偏控制系统模型,并进行了仿真,仿真结果表明模糊纠偏控制较PID纠偏控制鲁棒性好。

3) 采用2种控制方法进行纠偏控制实验,实验结果验证了仿真的正确性,在纠偏运动参数发生变化时,模糊控制器的纠偏精度达到了0.6 mm,满足缠绕工艺要求。

参考文献：

[1] 益小苏, 杜善义, 张立同. 复合材料手册[M]. 北京: 化学工业出版社, 2009: 387-388

Yi Xiaosu, Du Shanyi, Zhang Litong. Composite Handbook [M]. Beijing: Chemical Industry Press, 2009: 387-388 (in Chinese)

[2] Littlefield A, Hyland E, Andalora A, et al. Carbon Fiber/Thermoplastic Overwrapped Gun Tube [J]. Materials and Manufacturing Processes, 2006, 21(6): 573-578

[3] 史耀耀, 唐虹, 余强. 数控布带缠绕机关键技术[J]. 航空学报, 2008, 29(01): 233-239

Shi Yaoyao, Tang Hong, Yu Qiang. Key Technology of the NC Tape Winding Machine[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(01): 233-239 (in Chinese)

[4] 阎龙, 江伟, 史耀耀. 复合材料布带缠绕纠偏控制系统设计[J]. 宇航学报, 2012, 33(8): 1171-1176

Yan Long, Jiang Wei, Shi Yaoyao. Design of the Rectification Control System for Composites Tape Winding[J]. Journal of Astronautics, 2012, 33(8): 1171-1176 (in Chinese)

[5] Shin K, Kwon S, Kim S, et al. Feedforward Control of the Lateral Position of a Moving Web Using System Identification[C]∥Industry Applications Conference, 38th IAS Annual Meeting. Conference Record of the IEEE, 2003, 1: 345-351

[6] 权龙,李敏,姚李威,等. 核心器件冗余的低能耗电液伺服纠偏控制技术[J]. 机械工程学报, 2009(12): 59-64

Quan Long, Li Min, Yao Liwei, et al. Electro-Hydraulic Servo Edge Position Control Technology with Low Energy Lose and Key Devices Redundancy[J]. Journal of Mechanical Engineering, 2009(12): 59-64 (in Chinese)

[7] Young G, Shelton J, Kardamilas C. Modeling and Control of Multiple Web Spans Using State Estimation[J]. Journal of Dynamic Systems, Measurement, and Control, 1989, 111(3): 505-510

[8] Shin K, Kwon S. The Effect of Tension on the Lateral Dynamics and Control of a Moving Web[J]. IEEE Trans on Industry Applications, 2007, 43(2): 403-411

[9] 杨开平, 史耀耀, 何晓东, 等. 复合材料布带缠绕智能纠偏控制技术[J]. 航空学报, 2011, 32(7): 1318-1325

Yang Kaiping, Shi Yaoyao, He Xiaodong, et al. Controlling Technology of Intelligent Position Correcting in Winding Process of Composites[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(7): 1318-1325 (in Chinese)