一种改进的矩阵束模态参数估计方法
2014-03-25谭博侯玉郑华裴承鸣
谭博, 侯玉, 郑华, 裴承鸣
(1.西北工业大学 数据处理中心, 陕西 西安 710072; 2.中航工业西安飞机集团有限责任公司, 陕西 西安 710089)
结构模态参数是结构动力学的主要参数之一,具有简明、直观、物理概念清晰等优点。通过系统的结构模态参数可以建立相应的数学模型,进而根据载荷下的响应对设计进行必要的调整和修改。在工程应用中,实际观测到的信号一般是随机过程,且具有信噪比低、模态密集、有效样本短等特征,这样一来,对基于观测的模态参数估计方法就提出了近乎苛刻的要求。
矩阵束方法是20世纪80年代末、90年代初由Hua和Sarkar提出的一种模态参数估计方法,已经在飞行器、汽车、桥梁以及建筑物的设计中有了广泛的应用。但是,在实际应用当中发现,该方法的参数估计质量经常会受到诸如样本长度、信噪比等的影响。为此,本文结合随机减量技术对矩阵束方法进行了改进,并应用蒙特卡罗方法对改进后方法的数值性能进行了分析研究。
1 改进的矩阵束方法
单模态自由度线性系统运动微分方程为:
(1)
其位移响应x(t)为:
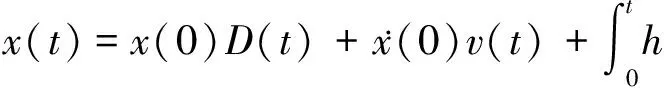
(2)
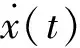
选取适当的A,选取响应中x(ti)=A的点,其中交点对应的时刻为ti(i=1,2,…)。由于是线性系统,对于自ti时刻起的响应x(t-ti)可以看成是由ti时刻的初位移、初速度和随机激励引起的强迫响应的三者线性叠加。可以由(3)式表达:
(3)

E[X(t)]=E[(x(0)|x(0)=A)]D(t)=AD(t)
(4)
上式表明子响应过程X(t)可以看做一个初位移为A,初速度为零的自由振动响应。对于多模态振动系统,若其系统是线性非时变的,可看做是2个或多个单模态自由度系统的线性叠加。
所得子响应过程X(t)可以表示为如下M个模态的指数函数的线性组合:
(5)
式中:s(t)为系统响应,n(t)为残留的系统噪声,t∈[0,T],T为最大观测时间。对第i个模态,算子si=-αi+jωi可用于表示模态的频率和阻尼比系数,其中ωi为角频率,αi为阻尼比系数。
(5)式的离散时间形式为:
(6)
式中:zi=exp(siTs)为系统响应的极点,Ts为采样周期,k=0,1,2,…N,N为最大采样点数。
由X(t)可以构造如下的Hankel矩阵:
(7)
式中:L为矩阵束参数,通常取值位于N/4~N/3之间。
对矩阵Y进行奇异值分解,得到:
X=UDVT
(8)
式中:U为(N-L)×(N-L)的正交矩阵;V为(L+1)×(L+1)的正交矩阵;D为(N-L)×(L+1)的对角阵,主对角线上的元素为Y的奇异值。
在已知模态个数M的情况下由D的前M个较大的非零奇异值形成如下新的矩阵D′:
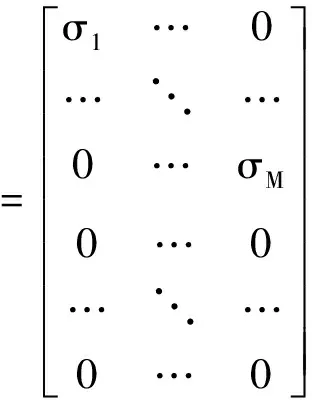
(9)
D′的前M行为一个由σ1…σM构成的M×M维的对角阵,其余行均为0。
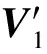
(10)
(11)
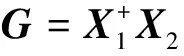
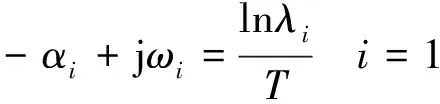
(12)
2 计算机仿真结果及分析
工程中采集得到的信号总是存在噪声影响,信噪比的大小会直接影响矩阵束方法的计算精度。本节将通过仿真信号对矩阵束方法在噪声环境下的数值性能进行研究。设置一个双模态自由度系统,模态参数分别设置为:f1=11 Hz,f2=17 Hz,d1=0.05,d2=0.03。使用矩阵束方法对加噪后的信号进行模态参数估计运算,并对计算结果进行统计,表1显示的是1 000次计算的最终统计结果。

表1 不同信噪比下矩阵束方法的计算结果
由表1可以明显看出,矩阵束方法估计所得频率受噪声影响较小,随着信噪比下降没有发生明显变化,而估计所得阻尼比系数随着信噪比下降有较大幅度变化,在噪声能量和加噪前的原始信号能量相等的情况下,估计值的误差甚至达到了真实值的2~3倍,这会影响矩阵束方法的工程应用。
通过仿真实验结果可以看出,在其余条件均保持不变,仅改变信噪比的情况下,矩阵束方法所得的阻尼估计结果会产生较大的波动。
为减轻噪声对矩阵束方法阻尼比估计结果的不良影响,下面将使用引进的矩阵束方法对含有噪声的信号进行处理。同时加入常用的带通滤波器降噪方法的计算结果以便于和本文方法进行横向比较,其统计结果分别如表2和表3所示。
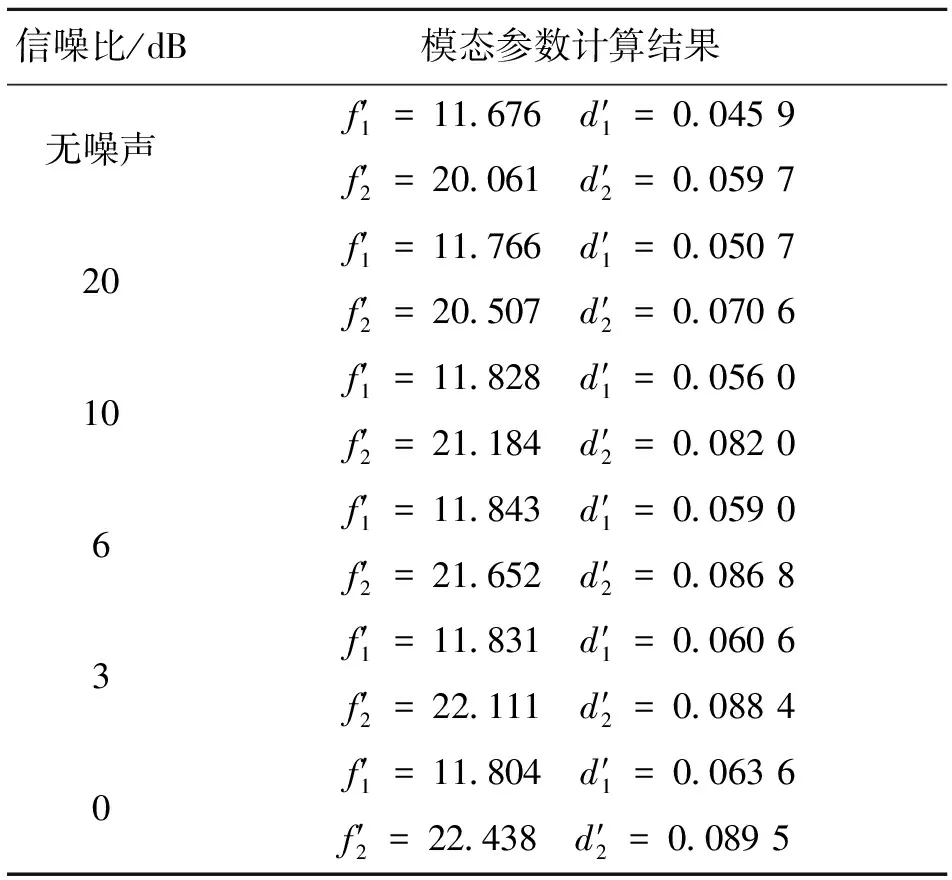
表2 通过带通滤波器处理后的计算结果
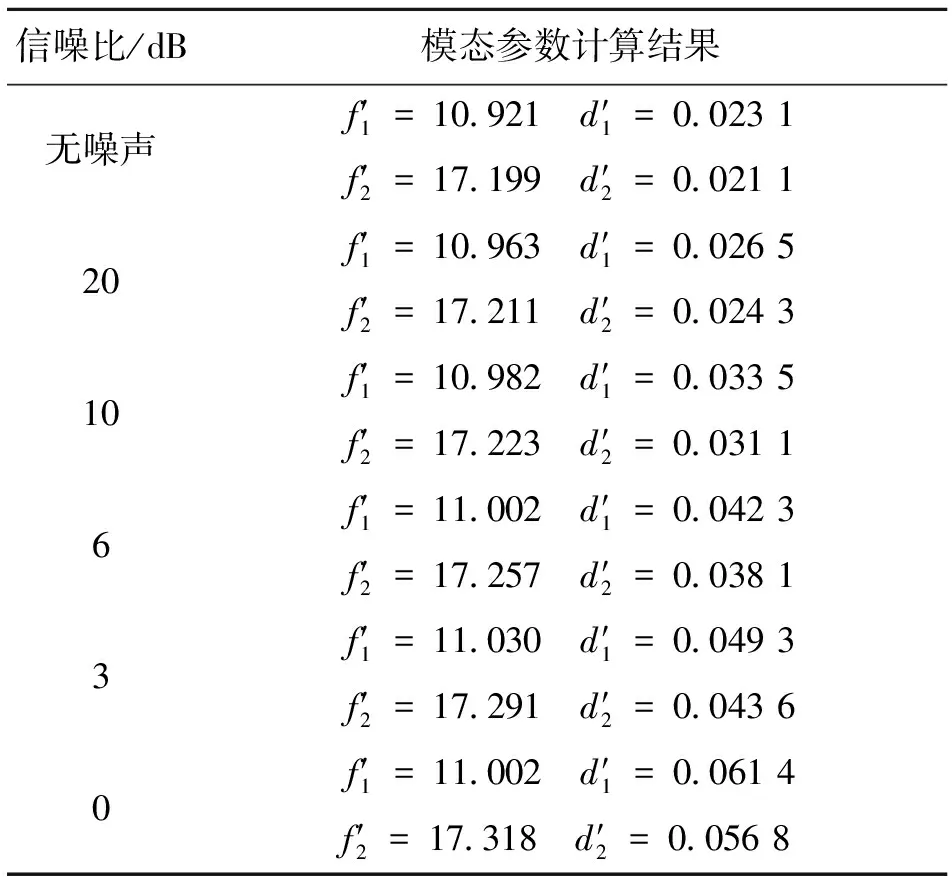
表3 改进的矩阵束方法的计算结果
由表1和表2的对比可以看出,通过带通滤波器以后,信号中噪声的能量受到抑制,尽管计算所得的阻尼比随着噪声能量的增大依然有所增加,但是增加幅度明显比未经处理的信号得到的结果要小,在噪声能量和加噪前原始信号能量相等的情况下,计算结果的误差约为真实值的一半,计算精度已经有所改善。但可以注意到,尽管阻尼比的计算精度有了明显提高,但是计算所得的频率同真值相比的差距反而增大,因此仅通过带通滤波器不能很好地改善矩阵束方法的数值性能。
下面将使用本文方法对数据进行处理,并对计算结果进行统计。
由表3可以看出,本文方法的计算精度与传统的矩阵束方法相比有大幅的提高,其计算频率的最大误差不到2%;当原始信号能量与噪声能量相等的时候,其计算阻尼的误差约为20%,与带通滤波器处理后的计算结果相比,精度有进一步的提高。
为了进一步研究3种方法的数值性能,下面将以阻尼比为0 dB,即噪声和原始信号能量相等的情况为例,研究3种方法在此信噪比下1 000次计算结果的分布情况。
图1和图2展示的为1 000次计算结果的统计分布,真实频率为11 Hz,真实阻尼比系数为0.05。图中,梗状图为计算结果(阻尼或频率)分布,实线为高斯拟合曲线,横轴中点均为真实值;由图a)至图c)依次对应矩阵方法、带有滤波器的矩阵束方法以及本文方法的计算结果。
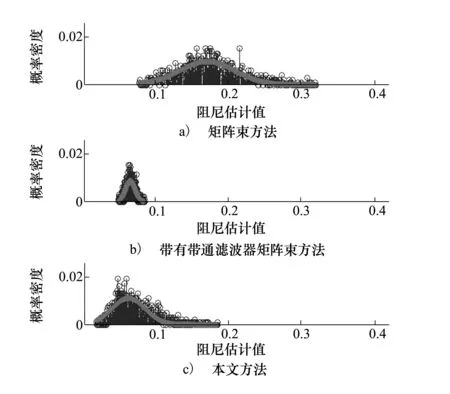
图1 计算阻尼分布
由图1中3种方法结果的对比可以看出,矩阵束法的计算结果整体偏离真实值较远,而且分布较散,这表明每次的计算值会在一个较大的范围内波动,不利于通过计算确定模态的参数。而引入通滤波器后信号的计算结果分布集中,且计算的阻尼比系数与真值的差明显缩小,矩阵束方法的数值性能得到了改善。本文方法的结算结果尽管不如第二种方法所得结果理想,但是其也较为集中分布在真实值附近,相比传统的矩阵束方法,其具有更好的数值性能。
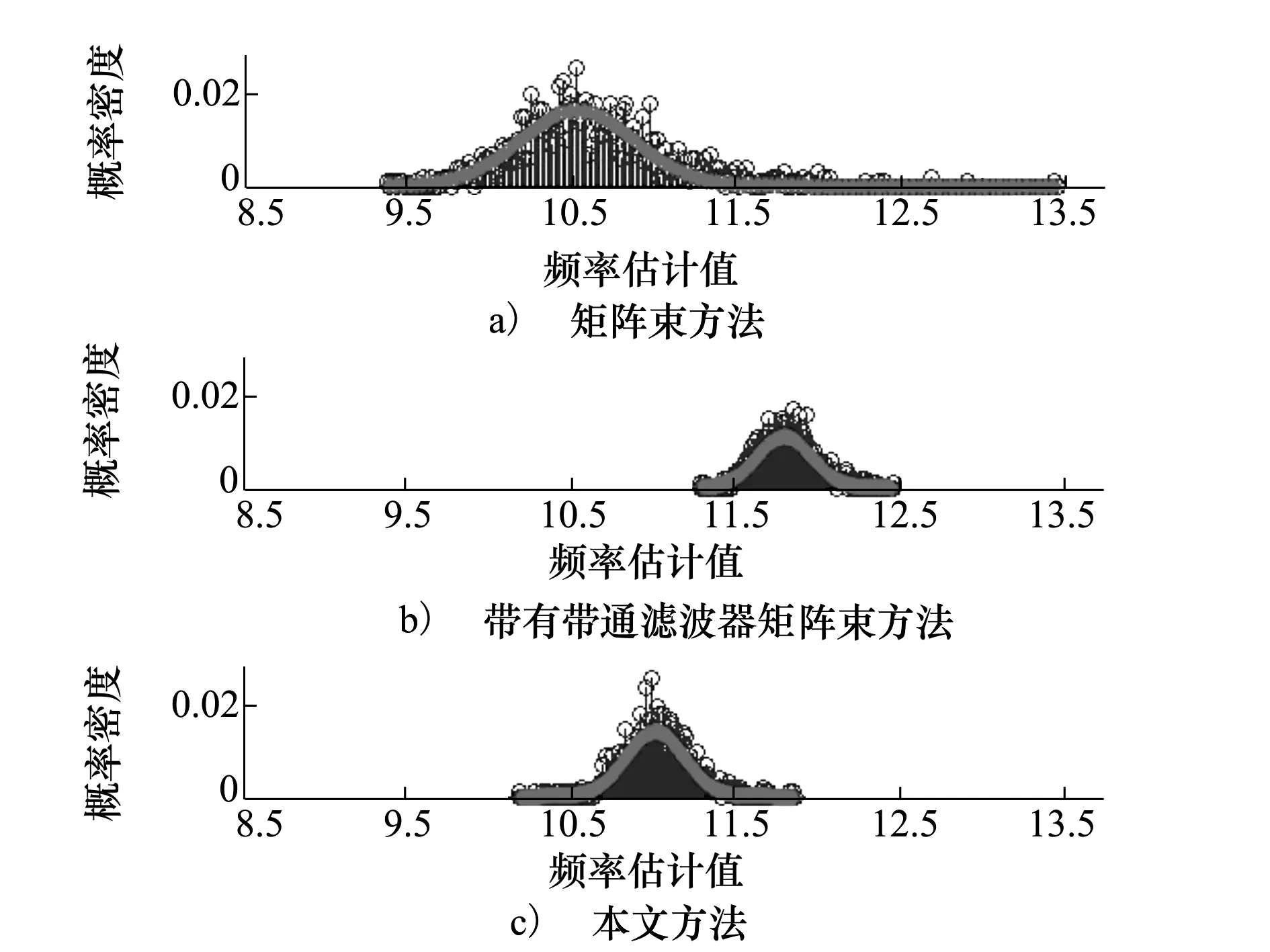
图2 计算频率分布
由图2可以看出,在频率的估计方面。矩阵束方法和引入滤波器的矩阵束方法的计算结果均与真实值有一定的差异,相比之下,带有滤波器矩阵束方法的结果分布更加集中,略微地改善了矩阵束方法的估计频率结果精度,但是仍然和真实值相差较大,而本文方法所得结果更为理想,其频率的精度较前两种方法的结果有明显提高。
综上所述,本文方法可以有效的提升矩阵束方法的参数估计结果的精度,与带通滤波器这种传统的降噪方法相比也具有一定的优势。
3 结 论
借助随机减量技术,本文提出了一种改进的矩阵束方法,经计算机仿真及蒙特卡罗统计分析,验证了本文方法在模态参数估计方面的合理性和有效性。通过提高矩阵束方法的计算结果精度,还可进一步用于解决模态参数估计中的一些其他常见问题,如密集模态等。可以预见,该方法对于包括结构颤振在内的航空航天领域有着重要的工程实用意义。
参考文献:
[1] Thomas A J, Chard J, John E, Davies A, Francis M. Defining a Bearing Replacement Strategy Using Monte Carlo Methods[J]. International Journal of Quality & Reliability Management, 2011, 28(2): 155-167
[2] Daniel Potts, Manfred Tasche. Parameter Estimation for Nonincreasing Exponential Sums by Prony-like Methods[C]∥17thConference of the international Linear Algebra Society,Braunschweig,Germany, 2013: 1024-1039
[3] Chiu Jen Ku. Random Decrement Based Method for Modal Parameter Identification of a Dynamic System Using Acceleration Responses[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95: 389-410
[4] 朱瑞可,李兴源,王渝红,赵睿,胡楠,李宽. 基于矩阵束算法的谐波和间谐波参数估计[J]. 华东电力, 2012, 40(3): 388-391
Zhu Ruike, Li Xingyuan, Wang Yuhong, Zhao Rui, Hu Nan, Li Kuan. Parameter Identification of Harmonics and Interharmonics Based on Matrix Pencil Algorithm[J]. East China Electric Power, 2012, 40(3): 388-391 (in Chinese)
[5] 庄铭杰. 蒙特卡洛仿真在移动通信中的应用研究[J]. 计算机仿真, 2004, 21(11): 116-120
Zhuang Mingjie. Application of Monte-Carlo Simulation in Mobile Communications[J]. Computer Simulation, 2004, 21(11): 116-120 (in Chinese)
[6] 张敏,黄俐,李文雄,钟学赋. 大型结构模态参数识别研究[J]. 建筑科学与工程学报, 2013, 30(2): 49-54
Zhang Min, Huang Li, Li Wenxiong, Zhong Xuefu. Research on Modal Parameter Identification on Large-Scale Structure[J]. Journal of Architecture and Civil Engineering, 2013, 30(2): 49-54 (in Chinese)
[7] 徐利,邹传云,陈民,何毅. 基于矩阵束算法的极点提取分析[J]. 通信技术, 2012, 45(6): 58-60
Xu Li, Zou Chuanyun, Chen Min, He Yi. Analysis on Pole Extraction Based on Matrix Pencil Algorithm[J]. Communications Technology, 2012, 45(6): 58-60 (in Chinese)
