航空装备关键件微动疲劳寿命预测

杨茂胜，温德宏，王海东

（1.海军航空工程学院青岛校区，山东青岛266041；2.海军装备部，北京100012）

微动损伤普遍存在于机械行业、航空航天器、核反应堆等领域的紧密配合部件中，已成为大量关键零部件的主要祸患之一，被认为是工业中的癌症。在航空装备的一些关键件中，如阻拦索和滑轮组索各钢丝之间、阻拦机液压缸的螺栓连接；飞机上的隔框、桁条和蒙皮的搭接组合结构都比较容易发生微动疲劳损伤；在发动机中，相当一部分零部件都存在微动磨损情况，如各种榫联接结构、机匣的安装边螺栓联接、盘和轴过盈压配合联接等。微动疲劳会加速受微动作用构件的接触处表面及表层裂纹的萌生和扩展，从而大大降低部件的疲劳寿命，甚至造成灾难性事故。

对微动疲劳的研究，20世纪90年代以前主要集中在其机理方面。之后，关于寿命方面的研究才逐渐丰富起来。在微动磨损机理方面，早期的研究成果有：Godfrey粘着机理、Suh剥层磨损理论、Uhlig机械化学作用理论以及Feng 和Rightmire 的磨损速率变化理论。在微动疲劳寿命方面，文献[1]在对燕尾榫连接结构进行实验的基础上，提出了微动损伤综合参数的概念，以此来确定微动疲劳裂纹产生的位置，并将寿命拟合为以综合参数为自变量的预测公式；文献[2]在对Ti-6Al-4V 合金的微动疲劳寿命预测中，提出用Manson-Coffin 公式来估算材料的微动疲劳寿命，该方法形象直观，可实际操作难度较大；文献[3]提出采用断裂力学方法进行微动疲劳寿命的预测，该方法认为应力奇异区或应力集中点可能为裂纹萌生位置；何明鉴等[4]提出附加应力法，将微动损伤作为一种应力附加在远场应力上，用这个总应力建立微动疲劳S-N 曲线。该模型简单易用，但是获得S-N 曲线需要大量的试验数据。以上研究所涉及的参数比较多，计算难度较大，且多是对结构的形成寿命或总寿命进行估算，而对于微动疲劳中占主导作用的裂纹扩展寿命研究较少。

针对以上分析中的不足，本文研究了航空装备关键件的微动损伤机理，并通过接触应力分析，构建了圆柱/平面接触结构微动疲劳裂纹扩展寿命预测模型。

1 微动疲劳损伤机理分析

在微动疲劳损伤机理方面，各国学者进行了大量的研究。但因其本身的复杂性、影响因素的多样性以及实验条件的变化性造成了各种观点的分散性。

本研究利用扫描电镜对实验件进行观察分析，认为微动疲劳损伤机理可按以下所示的发展阶段来解释。在微动损伤的初期，见图1 a），表面划痕与微动方向相同，而通常情况下微动疲劳造成的断裂损伤与微动方向垂直，因而初期的划痕只是一个短暂的宏观现象，不会导致破坏性裂纹的产生。在循环应力、接触应力和切向摩擦力共同形成的交变剪切应力作用下，材料表层反复经历塑性变形，产生类似冷作硬化的效果，随着微动的不断进行，塑性变形不断积累，位错密度不断增加，最终在接触应力最大的亚表层萌生疲劳微裂纹，见图1 b）。在微动磨损的协同作用下，裂纹间相互贯通，导致表层材料脱落，随着材料的脱落，微裂纹也逐渐消失，但随着材料脱落的延续，脱层材料不断增加并氧化，形成大面积的氧化颗粒，见图1 c）。氧化颗粒在交变应力的作用下，相互间产生挤压、磨擦，并向纵深方向扩展形成磨蚀坑，蚀坑底部受到硬质氧化磨屑的反复碾磨会变得高低不平，并产生较大的塑性变形，从而产生较大的应力集中，这样就在蚀坑底部萌生了疲劳裂纹，见图1 d）。

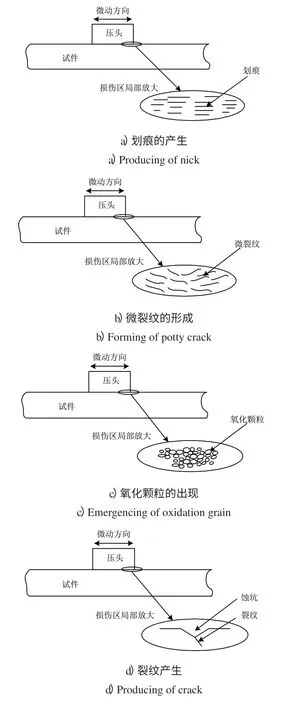
图1 微动疲劳损伤机理示意图Fig.1 Schematic of mechanism of fretting fatigue damage

2 微动接触有限元分析

2.1 结构模型

由于航空装备中容易受微动疲劳损伤的结构中，接触方式大多为柱面/平面接触，为此，本研究以飞机上的桁条和蒙皮间的搭接组合为研究对象。图2为圆柱/平面接触微动疲劳结构示意图，试件一端固定，一端受循环轴向应力σ，应力比R=0.06，接触压力P确保压头与试样之间的接触，切向力Q使得试样与压头之间保持一定的相对移动。试件和压头材料均为航空铝合金LY12CZ，弹性模量为68 GP，泊松比0.33。

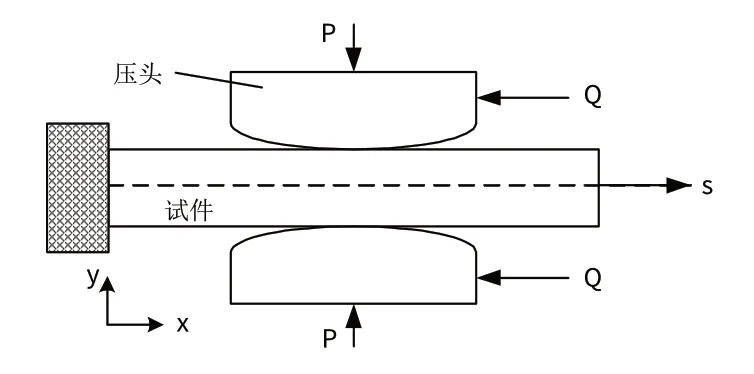
图2 微动疲劳结构示意图Fig.2 Schematic of a Fretting fatigue model

2.2 有限元全局模型

根据对称性，取整个结构的一半进行分析，由于压头和试件都处于平面应变状态，为简化计算，选择二维模型建模。试样底端在Y方向的位移为0，试样左端和压头左端在X方向的位移为0。另外，为了保证压头顶端各节点的位移相同，在该面上施加了多点约束（MPC）。模型采用4 节点平面应变单元[5-6]，接触区网格单元大小有2种，分别为中等尺寸24μm×24μm和精细尺寸12μm×12μm。分析模型选用ABAQUS Standard，压头底面作为接触主面，试样上表面为从面，摩擦系数为0.5。整个分析设3个分析步：第1步，在压头上施加正应力P=9.6 MPa；第2步，在试样一端施加最大轴向拉应力σ=225 MPa，同时在压头上施加最大切向应力Q=40.7 MPa；第3 步，在试样一端施加最小轴向拉应力σ=13.5 MPa，同时在压头上施加最小切向应力Q=-40.7 MPa。最终得到的全局有限元模型及网格划分，见图3。图4为第1步结束时的应力云图，可看到最大应力出现在接触表面的中心处。

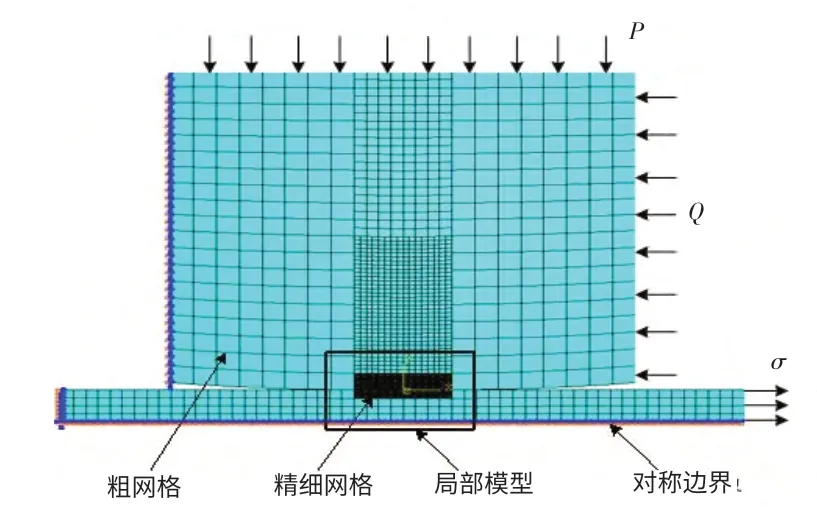
图3 有限元全局模型Fig.3 Global finite element model

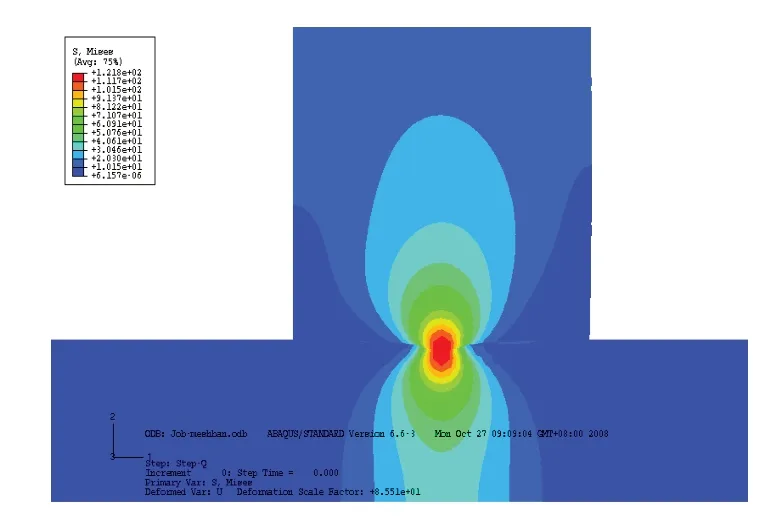
图4 应力云图Fig.4 Stress contours

2.3 有限元子模型

在微动分析中，压头和试件的接触部位是最重要的区域，因而有必要对接触区，尤其是接触边缘（裂纹通常在此处萌生），进行网格细化，以获得更为精确的局部应力、应变、位移场。ABAQUS 提供了子模型分析模块，可以在全局模型分析结果的基础上，使用细化网格对模型的局部作进一步分析，从而以较小的计算代价得到更精确的结果[7]。

为了提高计算效率，在使用子模型技术前，需要用到如下的收敛准则：

图5为有限元子模型，其接触区网格尺寸大小分2种，中等尺寸10 μm×10 μm和精细尺寸7 μm×7 μm。

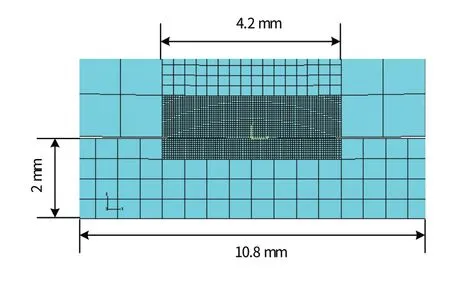
图5 有限元子模型Fig.5 Sub-model of the FEM

为了检验子模型的计算精度，引入边界条件误差εbc和离散误差εd的概念，表示为：

由于εbc和εd都有可能为正值也可能为负值，于是其误差收敛准则为：

式中，λ是0到1之间的数值，本文取λ=0.5。

由ABAQUS 全局模型和子模型所计算的边界条件误差和离散误差见表1，从中可看到2种误差绝对值都小于1%，达到了高精度级。这说明利用中等网格尺寸子模型和精细网格尺寸子模型计算的结果都能满足设计要求。因此，本文最终选择全局模型网格尺寸为24 μm×24 μm，子模型网格尺寸为10 μm×10 μm。

表1 边界条件误差和离散误差Tab.1 Boundary conditions and discrete errors

3 微动疲劳裂纹扩展寿命计算

3.1 裂纹扩展门槛值准则

微动疲劳情况下，疲劳裂纹形成后，其在材料中的扩展可分为2 个阶段：第1 阶段是在与拉应力成一定倾角的最大剪应力的方向扩展，在这一阶段内裂纹扩展速率和深度都非常小，因而在这个阶段消耗掉的疲劳寿命也相对比较低；第2阶段，裂纹沿着最大拉应力平面进行扩展，其扩展速率与深度都比第一阶段大得多，疲劳寿命也主要在这一阶段内消耗，这也是重点研究的一个阶段。

3.1.1 长裂纹扩展门槛值准则

长裂纹扩展门槛值准则是通过有效应力强度因子ΔKeff与材料抗扩展性能参数的对比建立起来的，即当ΔKeff值小于某一界限值时，裂纹基本上不扩展，该界限值称为长裂纹扩展门槛值。长裂纹扩展门槛值准则可表示为

式中，有效应力强度因子ΔKeff可用Walker 公式表示如下：

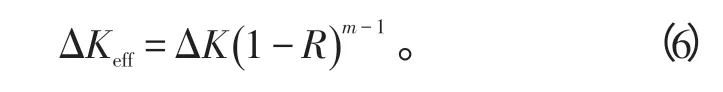
式（6）中：R是应力比；m是材料常数，其值通常在0到1之间，对于航空铝合金材料，m=0.61。

Cindie Giummarra[8]通过对疲劳裂纹扩展实验数据的拟合发现，对于铝合金，长裂纹扩展门槛值与循环应力比R之间存在如下的关系：

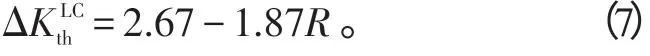
3.1.2 短裂纹扩展门槛值准则

在某些情况下，当有效应力强度因子ΔKeff小于长裂纹扩展门槛值时，裂纹也会扩展。为了解释这种情况，Kitagawa 用图6 来描述了光滑试件的断裂力学行为[8]。

图6 Kitagawa断裂行为示意图Fig.6 Schematic of Kitagawa diagram

图6中，倾斜直线代表长裂纹门槛应力值，水平直线代表传统光滑试件的疲劳极限σe，在水平直线或者倾斜直线以上的部分，则属于不稳定区域，裂纹会在此扩展；而在水平直线和倾斜直线以下的区域属于稳定区域，该处不会有裂纹的扩展。

2条直线的交点所对应的裂纹深度值l0为短裂纹参数，也即是长裂纹和短裂纹的分界值，其大小可表示为：

式（8）中，Y是裂纹形状参数，有效长裂纹扩展门槛值和疲劳极限值σe分别为：

式中，σ0为材料常数，即应力比R=0 时的疲劳极限值。

图7为短裂纹对ΔKth的影响。

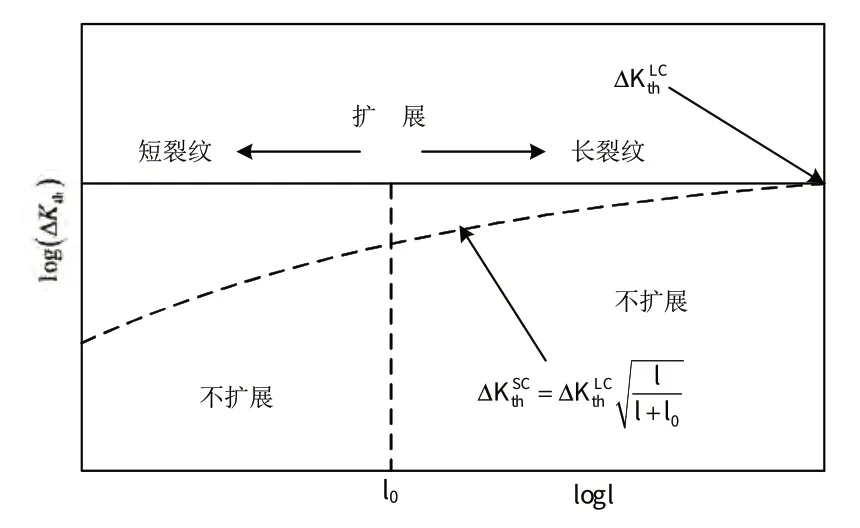
图7 短裂纹对ΔKth 的影响Fig.7 Short crack effect on ΔKth

从图6 及图7 中可以看出，当尺寸小于l0的裂纹在应力强度因子小于长裂纹扩展门槛值时，该裂纹也可能扩展，Nicholas T 等人通过研究建立了如下的短裂纹扩展门槛值准则[9]：

也可以用门槛应力值表示为

3.2 应力强度因子计算

如图8 所示，在FRANC2D/L 中重建子模型，其中压头用等效的正应力和剪应力来代替。整个模型为一矩形，其高度为试样厚度的一半（2 mm），长度L至少应该是最大裂纹长度的10倍，这样才能保证模型的边界不受因裂纹产生的应力集中影响。基于该原则，模型长度定为10.8 mm。根据对称性，模型下边在Y方向的位移为零，而该边的中点处在X方向的位移也为零。左右端的拉应力以及接触区的正应力σ(x,0)和剪应力τ(x,0)都由ABAQUS 子模型计算所得。文献[8]的研究表明，裂纹通常出现在接触区边缘，即x=a处，裂纹倾斜角为45°，因而在该处插入一初始裂纹，其长度为颗粒尺寸的2倍，局部放大后的初始裂纹见图9。

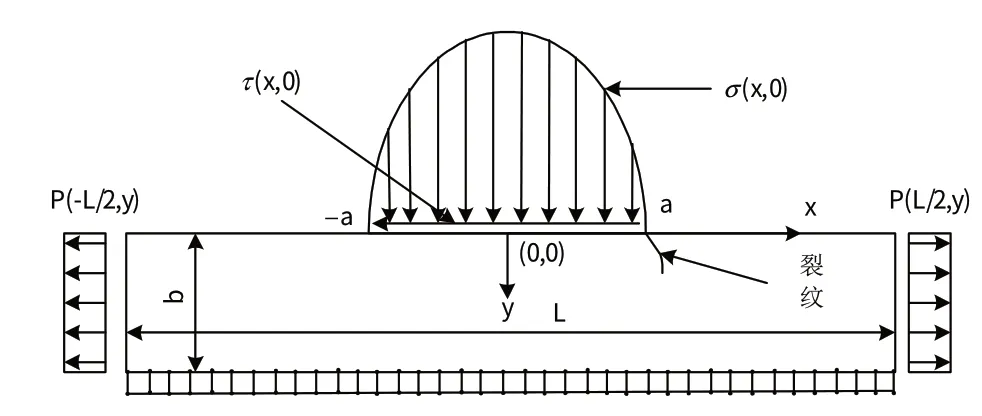
图8 FRANC2D/L中重建子模型Fig.8 Schematic of the sub-model in FRANC2D/L

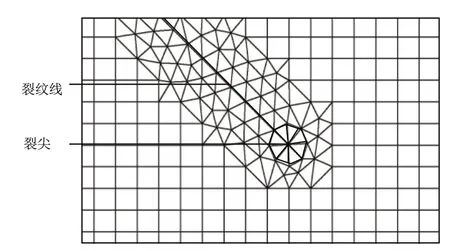
图9 FRANC2D/L中的初始裂纹Fig.9 Initial configuration of the crack in FRANC2D/L

裂尖的应力强度因子SIF是表征裂纹尖端附近应力强度的一个有效参量，可作为判断裂纹是否将进入失稳状态的一个指标。本文通过计算在复合型加载条件下二维裂纹的能量释放率来获得应力强度因子，其大小值与裂纹长度的关系历程可由FRANC2D/L中的裂纹扩展功能来实现，图10为裂纹的扩展路径。

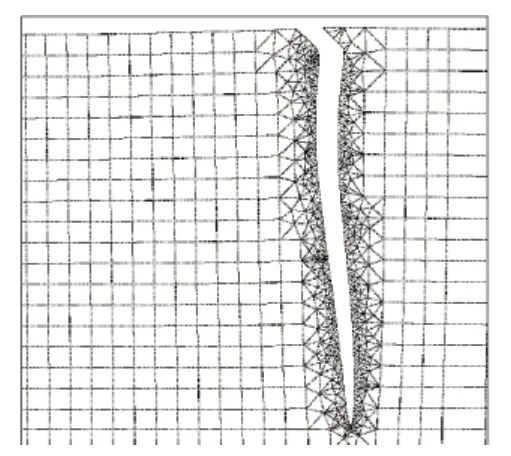
图10 FRANC2D/L中的裂纹扩展路径Fig.10 Moved crack in FRANC2D/L

3.3 裂纹扩展寿命计算模型

结合以上长、短裂纹扩展门槛值准则，以及应力强度因子的有关计算，建立了如下的微动疲劳裂纹扩展寿命计算模型，见图11。

模型中先输入初始裂纹长度l1，由FRANC2D 计算应力强度因子范围ΔK，结合应力比R分别计算有效应力强度因子范围ΔKeff、有效应力强度因子门槛值、疲劳极限σe以及长、短裂纹分界值l0，再根据长、短裂纹扩展门槛值准则，确定是按照长裂纹扩展行为还是按短裂纹扩展行为来分析计算，从而获得应力强度因子－裂纹长度关系曲线，并建立起应力强度因子影响系数β2与裂纹长度的对应关系。为了考虑应力比对疲劳寿命的影响，裂纹扩展速率公式皆采用Wallker公式，表示为

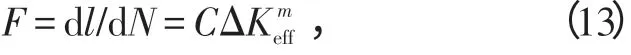
其中，C、m为材料常数，由试验拟合得到。

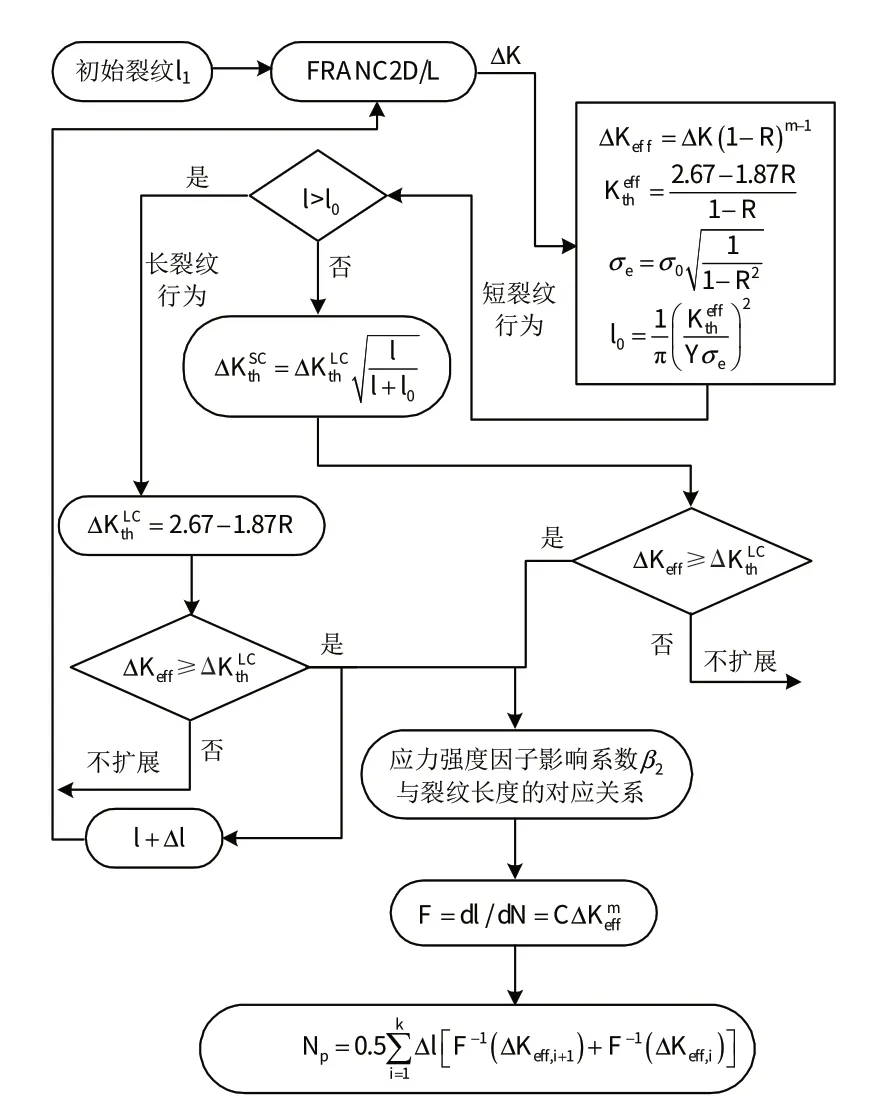
图11 裂纹扩展寿命计算模型Fig.11 Flow chart summarizing the crack growth model

由于有效应力强度因子无法写成裂纹长度的显示表达式，因而无法用积分公式直接求得寿命，但可以按定积分的定义，通过选择微小增量Δl，然后逐步地计算ΔN。具体的计算由AFGROW 软件来实现，最终得到的寿命计算公式：

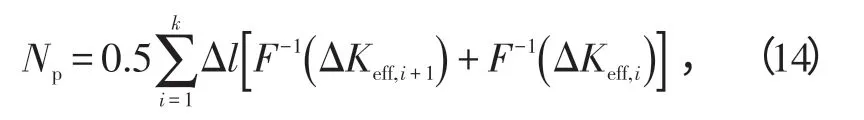
式中，Δl的大小在2~5 μm之间。因为在Δl=2 μm和Δl=5 μm时计算出的裂纹扩展寿命是比较接近的，本文选择Δl=2 μm[10]。

3.4 参数确定

将实验所选用的应力比R=0.06[11]代入相应各式中可求得以下参数值。

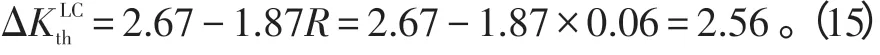
3.4.2 长、短裂纹分界值l0

将R=0.06，σ0=119 MPa 代入式（7）和式（8），可求得=2.72 MPa和σe=130.22 MPa，再将他们代入式（9）可求得

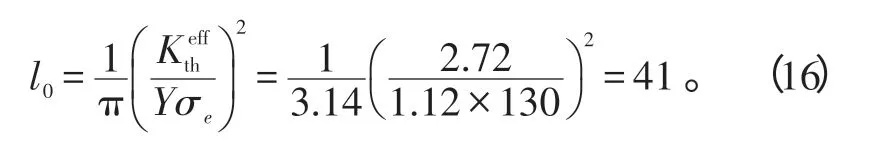
3.4.3 材料常数C、m

由实验得到的航空铝合金材料裂纹扩展速率－应力强度因子对应关系拟合得到的裂纹扩展速率公式的表达式为

经变换可得

于是，有C=5.945 6×10-9，m=2.686。

3.5 结果分析

将试验中循环次数为100 000所对应的裂纹长度38.2 μm作为初始裂纹长度，另外将裂纹扩展常数C、m、应力值、应力比等所需参数输入AFGROW，便可求得航空铝合金微动疲劳扩展寿命与裂纹长度的对应关系曲线，如图11 所示。从图中可知，预测的微动疲劳扩展寿命值为72 200，比试验值97 037偏小，误差为-25.6%。误差形成的原因可能是Walker 公式中的材料常数是通过试验数据拟合得到的，而试验中由于测量精度和人为因素的影响，使得拟合结果与真实结果之间存在一定的偏差。

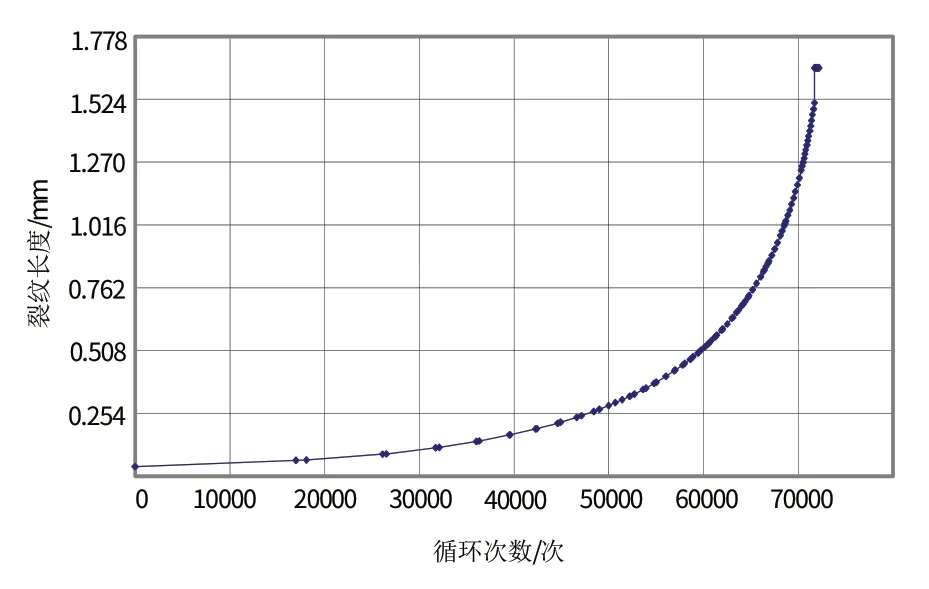
图12 微动疲劳裂纹扩展寿命预测值与裂纹长度关系Fig.12 Fretting fatigue life of prediction as a function of crack length

4 结论

本文分析了微动疲劳损伤机理，计算了接触区应力分布，采用断裂力学的方法建立了航空装备关键件微动疲劳裂纹扩展寿命预测模型，经分析得到如下结论：

1）航空铝合金材料的微动疲劳损伤包括划痕的产生、微裂纹的形成、氧化颗粒的出现、裂纹从蚀坑底部产生4个过程；

2）基于ABAQUS 有限元软件，构建了圆柱/平面接触微动疲劳结构的全局模型和子模型，通过边界条件误差和离散误差分析，使计算精度和计算效率都有显著提高；

3）基于断裂力学理论，引入应力强度因子影响系数β，建立了微动疲劳裂纹扩展寿命预测模型，运用所建模型将计算的寿命值与试验值进行比较，结果比较吻合，证明了本文所建模型及算法的有效性。

[1] RUIZ C，BODDINGTON P H B，CHEN C.An investing ation of fatigue and fretting in a dovetail joint[J]. Experimental Mechanics，1998，24（4）：208-217.

[2] CHRISTOPHER D LYKINS，SHANKAR MALL，VINOD JAIN.An evaluation of parameters for predicting fretting fatigue crack initiation[J].International Journal of Fatigue，2000，22（2）：703-716.

[3] GOLDEN P J，CALCATERRA J R.A fracture mechanics life prediction methodology applied to dovetail fretting[J].Tribology International，2006，39（1）：1-9.

[4] 何明鉴，张德志. 确定微动疲劳寿命的附加应力法[J].航空发动机，2003，29（3）：27-29.

HE MINGJIAN，ZHANG DEZHI. The method of attached stress for determining fretting fatigue life[J].Aeroengine，2003，29（3）：27-29.（in Chinese）

[5] 陈跃良，杨茂胜，胡家林.飞机结构搭接件微动疲劳研究的关键技术[J].海军航空工程学院学报，2008，23（4）：361-366.

CHEN YUELIANG，YANG MAOSHENG，HU JIALIN.Research on the key technology of fretting fatigue in lap joints of aircraft structure[J]. Naval Aeronautical And Astronautical University，2008，23（4）：361-366.（in Chinese）

[6] 杨茂胜，陈跃良，毕玉泉.基于寿命预测模型的微动疲劳影响因素研究[J]. 海军航空工程学院学报，2012，27（1）：39-44.

YANG MAOSHENG， CHEN YUELIANG， BI YUQUAN.Studying on influencing factors of fretting fatigue based on life prediction model[J]. Naval Aeronautical and Astronautical University，2012，27（1）：39-44.（in Chinese）

[7] YHKSULL H I. Effects of shot-peening on high cycle fretting fatigue behavior of Ti-6Al-4V[D]. Washington：Air force institute of technology，2002.

[8] CINDIE GIUMMARRA.Fretting fatigue of 2XXX series aerospace aluminum alloys[D]. New York：Rensselaer Polytechnic Institute，2003.

[9] HASSAN A FADAG.An investigation of the propagation behavior of fretting fatigue cracks in Ti-6Al-4V[D]. Dayton：University of Dayton，2005.

[10]NICHOLAS T，HUSTON A，KOHN，et al.A fracture mechanics methodology assessment for fretting fatigue[J].International Journal of Fatigue，2003，25（2）：1369-1077.

[11]杨茂胜.微动对LY12CZ铝合金疲劳性能的影响[D].烟台：海军航空工程学院，2011.

YANG MAOSHENG.The effect of fretting on fatigue performance of LY12CZ aluminum alloy[D]. Yantai：Naval Aeronautical And Astronautical University，2011.（in Chinese）