基于滑模自适应控制的不确定混沌系统修正函数投影同步

余名哲，张友安，吴华丽

（海军航空工程学院控制工程系，山东烟台264001）

基于滑模自适应控制的不确定混沌系统修正函数投影同步

余名哲，张友安，吴华丽

（海军航空工程学院控制工程系，山东烟台264001）

研究了一类不确定混沌系统的修正函数投影同步。首先，设计了一类滑模曲面；基于该曲面设计了同步控制器，并采用自适应技术设计了自适应律对不确定参数进行逼近。在一定条件下，该同步控制方案可以实现2个不确定异结构混沌系统的修正函数投影同步。然后，为保证合适的控制量，对控制增益进行了优化。从同步效果来看，所设计的控制器对混沌系统的不确定项的影响具有较强的鲁棒性。最后，数值仿真验证了该控制器的有效性和可行性。

混沌系统；修正函数投影同步；滑模自适应控制；鲁棒性

混沌现象在工程实践中特别是在生物医学、保密通信、图像加密、信息处理、光学、化学工程、航天等领域获得了广泛的应用。在这些领域，实际问题的方程建模及解法很多都体现出了混沌特性[1-3]，由此引起了国内外学者们的高度关注。从1990年OGY控制方法提出以来，混沌的控制和同步方法层出不穷，但是大多基于理想的混沌层面[4-5]。实际系统中，理想的混沌系统几乎是不存在的，工程中要面对的往往是具有种种不确定性因素的非线性系统，比如系统中含有不确定参数、结构不确定项、内部及外部扰动等。这些不确定性因素有可能是未知的，也有可能是时变的[6-7]。这就要求研究混沌系统时，要充分考虑有不确定性因素情况下如何保证系统同步的鲁棒性，即克服不确定性对混沌系统控制的影响。

目前，混沌同步的方式也越来越多样化，有反同步、相同步、滞后同步、投影同步、函数同步等。投影同步是指驱动与响应系统同步向量之比为一个常数，这种同步方式相较来说提高了一定的同步复杂性，但其结构还是比较简单。有学者将比例常数扩展为函数或者常数阵，这样就构成了函数投影同步或修正投影同步。更有学者将常数阵扩展成比例函数矩阵，提出了一种新的同步方法，即修正函数投影同步[8-9]，就是将驱动与响应系统的同步向量按任意给定的比例函数矩阵关系进行同步。将该同步方式运用于通信时，因加入了第三方不可预知的比例函数，从而增加了传输过程中混沌信号抗破译的难度。因此，修正函数投影同步具有重要的研究前景和现实意义。

在控制方法中，自适应控制由于其良好的鲁棒控制性能，对混沌系统中的不确定部分进行自适应估计是十分适用的。另外，滑模变结构控制也因为其实现简单，对系统参数和内部及外部干扰具有很好的不敏感性，即具有较强鲁棒性的优点，对不确定系统进行控制也非常合适。本文采用自适应控制和滑模变结构控制相结合的控制方法对混沌系统进行了函数修正投影同步的研究，并依据Lyapunov稳定性理论，设计了同步控制器与相应的自适应律，并对控制增益进行优化[10]。本文采用的优化增益方法与文献[10]比，没有考虑非线性项的假定问题，直接设定一个常数，更为便捷。仿真结果表明，该控制策略响应速度快，具有较强的抗干扰能力，并且具有较高的实用价值。

1 问题描述和模型建立

考虑如下混沌系统：

构建引入控制输入的响应系统为

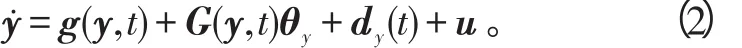
式（1）、（2）中：x,y∈ℝn为系统状态向量；f(x,t)、g(y,t)为光滑的非线性函数向量；F(x,t),G(y,t)∈ℝn×n为已知的矩阵函数；θx,θy∈ℝn和dx(t)、dy(t)分别为驱动系统和响应系统的未知常数项与扰动项，且假设扰动项均有界；u=[u1,u2,…,un]T为系统的输入控制量。

[8]定义驱动和响应系统的修正函数投影同步误差为：

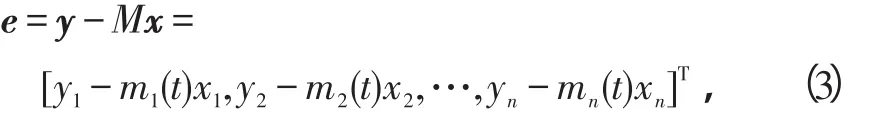
当使得lti→m∞‖e‖=lti→m∞‖y-Mx‖=0，e=[e1,e2,…,ei,…,en]T为系统误差向量。称为驱动系统与响应系统达到修正函数投影同步。

定义：比例函数矩阵

式中，mi(t)为连续可微的有界函数。（注：当m1(t)=m2(t)=…=mn(t)时退化为函数投影同步）。

对误差式（3）左右两边关于时间求导，可以得到同步误差系统为

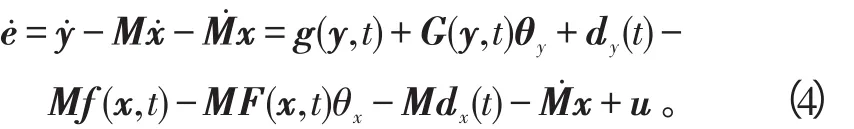
可见，在加入比例函数矩阵之后，系统的误差系统变为非常复杂。也就是，说应用于混沌通信的时候，抗破译能力将大为提高。

本文的目的就是要设计修正函数投影同步控制器u，使得当t→+∞时，有‖e‖→0。

注释：当f(·)≠g(·)，F(·)≠G(·)时，为混沌系统之间的异结构同步；当f(·)=g(·)，F(·)=G(·)，为同结构系统之间的同步。

2 同步控制器与自适应律设计

选取如下滑模面：

式中，c∈ℝn×n，为大于0的设计参数矩阵。为简单起见，将矩阵c取为对角阵，其且元素均为正常数。

对式（5）两边求导，并将式（4）代入，得到

现在给出定义：d(t)=dy(t)-Mdx(t)，对于实际系统来说，干扰一般是有界的，又由于比例函数mi有界，可知扰动向量d中的元素di(t)也是有界的，此处假设di(t)上界di*未知。

设计同步控制器为如下形式：

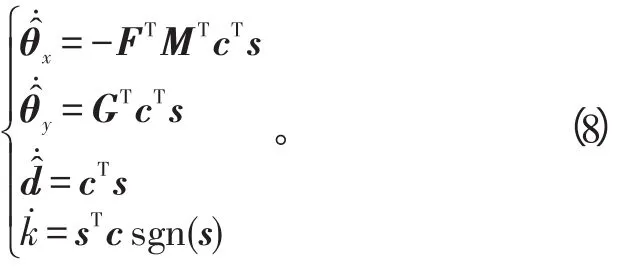
定理1：在同步控制器（8）和自适应律（9）的控制作用下，驱动系统和响应系统将达到修正函数投影同步。即当t→+∞时，‖e‖→0。

证明：将设计的控制律式（7）代入式（6），得到

参考文献[10]优化控制强度的方法，设计如下的Lyapunov函数：

俄国临时政府对待唐努乌梁海问题的态度和沙皇政府相同。外蒙古因为俄国侵占唐努乌梁海，一直与俄国存在矛盾，曾于1915年与之交涉，但俄方态度强硬。之后，克穆齐克旗旗总管巴彦巴达尔呼向乌城佐理专员洪桢呈文，请求中央政府帮助解决唐努乌梁海问题，陈毅建议中央政府采取强硬态度，带兵前往唐努乌梁海，但中国政府没有采纳。在俄国十月革命爆发之前，由于态度软弱，中国政府与俄国的种种交涉也毫无结果。

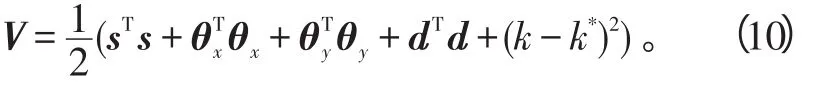
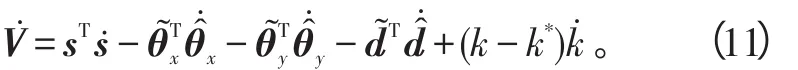
将式（10）和设计的自适应律（8）代入式（11）：

式（12）中：cmin为参数矩阵c的最小特征值；‖·‖p的角标p表示p范数。

根据Lyapunov稳定性理论，结合Barbalat引理，可确定滑模曲面‖s‖将渐近收敛到0。从任意初始条件出发的误差状态将收敛到滑模曲面‖s‖=0上，即在所设计的控制器和选择的自适应律的作用下，驱动系统与响应系统将达到修正函数投影同步。

3 数值仿真及分析

选取2个实际的混沌系统分别作为驱动系统和响应系统来说明控制策略的有效性。以不确定Lorenz混沌系统和Lü氏混沌系统的修正函数投影同步为例。选择Lorenz混沌系统作为驱动系统：

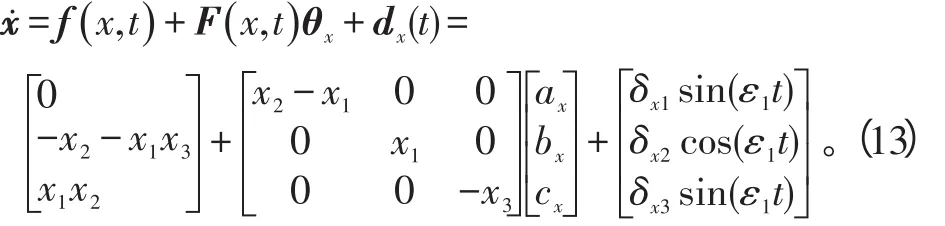
当式（13）中参数选取a1=10、b1=28、c1=8 3时，系统表现出混沌状态。

选取Lü氏混沌系统加入控制输入构建响应系统：

当参数选取a2=36、b2=20、c2=3时，Lü系统表现出混沌状态。ε1、ε2为时变系数。接下来选择比例函数矩阵，要注意在选择的时候函数不能为零。

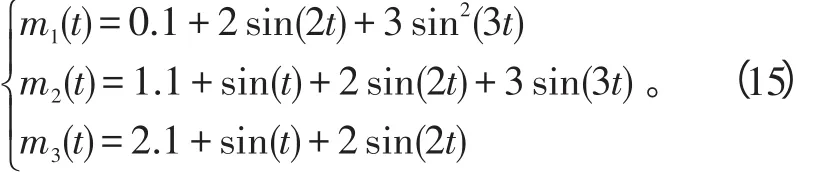
由定理1可以得到系统的控制律：

将给定的比例函数阵式M的分量代入式（16）得到具体系统同步控制律。定理1还可以得到不确定项各自的自适应律。

选取驱动系统和响应系统的初值为(x1(0),x2(0),x3(0))=(1,0,0.5)，(y1(0),y2(0),y3(0))=(0.5,1,0.5)，选取ci=2，r=30，扰动幅值δxi=0.5，δyi=0.8，待定控制强度的初始值=(1,1,1),(i=1,2,3)，自适应参数向量初值(10,30,20)，得到如图1～4的仿真结果。

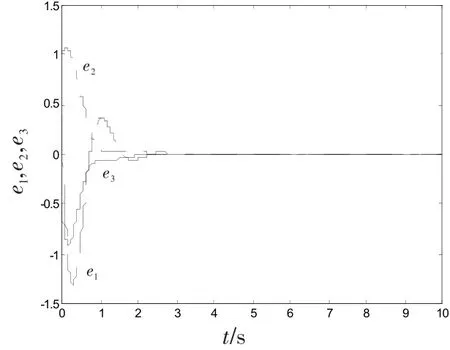
图1施加控制的系统同步误差曲线Fig.1 States of error system with control

图2控制增益k1随时间变化曲线Fig.2 Curve of the control gaink1

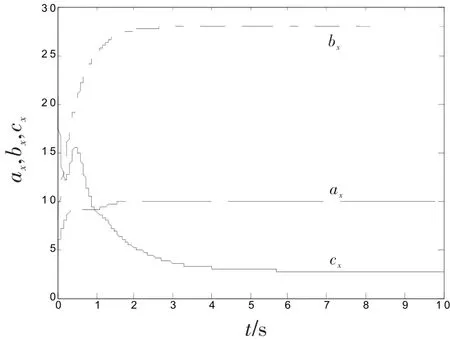
图3驱动系统不确定参数自适应变化曲线Fig.3 Adaptive parameters of drive system

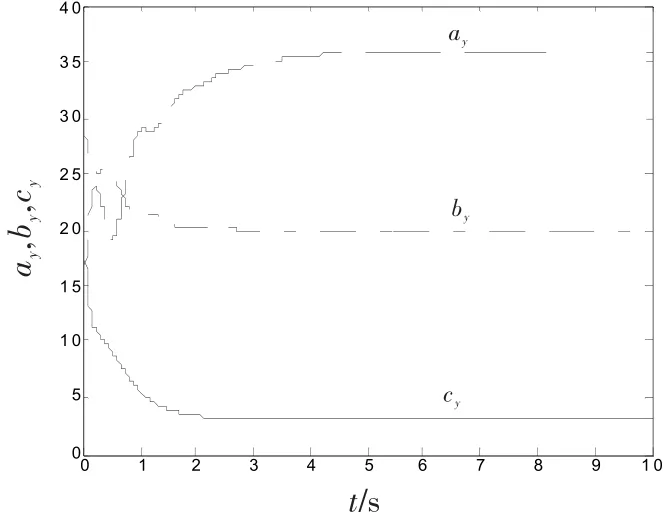
图4响应系统不确定参数自适应变化曲线Fig.4 Adaptive parameters of response system

仿真结果证明，控制器在有限时间内很好地将同步误差收敛到零，系统渐近稳定，也就是说驱动和响应系统达到了修正函数投影同步。

4 结论

本文针对受扰且含有不确定参数的混沌系统修正函数投影同步问题设计了控制策略。该策略基于Lyapunov稳定性理论，选择自适应控制方法，设计了参数自适应律，对系统不确定项进行了估计，为了克服干扰的影响设计了具有较强鲁棒性的滑模曲面，并根据滑模可达条件设计自适应同步控制器。该控制器将系统在空间中的轨线都能收敛到滑模面上，在其作用下，驱动系统和响应系统实现了修正函数投影同步。该方法对异结构和同结构的混沌系统具有一般性，不仅对外界或内部干扰具有较好的鲁棒性能，而且对控制增益进行了优化。数学推理和仿真分析验证了该方法的有效性。

参考文献：

[1]DEEPAK KUMAR LAI，SWARUP K S.Modeling and simulation of chaotic phenomena in electrical power systems[J].Applied Soft Computing，2011，11（1）：103-110.

[2]刘月东，韩锐，翟景春.非线性科学中的混沌[J].海军航空工程学院学报，2007，22（1）：177-180. LIU YUEDONG，HAN RUI，ZHAI JINGCHUN.The chaos theory nonlinear science[J].Journal of Naval Aeronautical and Astronautical University，2007，22（1）：177-180.（in Chinese）

[3]王焱，宋召青，刘晓，等.一种自适应滑模控制算法在四旋冀无人飞行器中的应用[J].海军航空工程学院学报，2013，28（5）：471-474. WANG YAN，SONG ZHAOQING，LIU XIAO，et al.Application of one self-adaption slide mode control method in unmanned acrial vehicle of four rotor[J].Journal of Naval Aeronautical and Astronautical University，2013，28（5）：471-474.（in Chinese）

[4]EDWARD OTT，CELSO GREBOGI，JAMES AYORKE. Controlling chaos[J].Physical Review Letters，1990，64（11）：1196-1199.

[5]HONGYUE DU，QINGSHUANG ZENG，CHANGHONG WANG，et al.Function projective synchronization in coupled chaotic systems[J].Nonlinear Analysis：Real WorldApplications，2010，11（2）：705-712.

[6]周爱军.不确定混沌系统的控制与同步方法研究[D].大连：大连海事大学，2012. ZHOU AIJUN.Research on control and synchronization methods for uncertain chaotic systems[D].Dalian：Dalian Maritime University，2012.（in Chinese）

[7]陈强，任雪梅，那靖.参数不确定混沌系统的自适应Backstepping控制[J].北京理工大学学报，2011，31（2）：158-162. CHEN QING，REN XUEMEI，NA JING.Adaptive backstepping control of chaotic system with uncertain parameters[J].Beijing Institute of Technology，2011，31（2）：158-162.（in Chinese）

[8]李建芬，李农.一类混沌系统的修正函数投影同步[J].物理学报，2011，60（8）：080507-1-5. LI JIANFEN，LI NONG.Modified function projective synchronization of a class of chaotic systems[J].Acta Physica Sinica，2011，60（8）：080507-1-5.（in Chinese）

[9]邓玮，方洁，吴振军，等.含有不确定项的混沌系统自适应修正函数投影同步[J].物理学报，2012，61（14）：140503-1-6. DENG WEI，FANG JIE，WU ZHENJUN，et al.Adaptive modified function projective synchronization of a class of chaotic systems with uncertainties[J].Acta Physica Sinica，2012，61（14）：140503-1-6.（in Chinese）

[10]张昭晗，高金峰.参数不确定异结构混沌系统的自适应同步控制[J].郑州大学学报：工学版，2011，32（6）：117-120. ZHANG ZHAOHAN，GAO JINFENG.Synchronization and control between different chaotic systems with uncertain parameters[J].Journal of Zhengzhou University：Engineering Science，2011，32（6）：117-120.（in Chinese）

Modified Function Projective Synchronization Base on Sliding Mode Adaptive Control for Chaotic Systems with Uncertainties

YU Ming-zhe,ZHANG You-an,WU Hua-li
（Department of Control Engineering,NAAU,Yantai Shandong 264001,China）

A modified function projective synchronization of a class of chaotic systems with uncertainties was investigated. Firstly,a sliding mode was designed based on the sliding mode,the synchronization controller was designed,and the adaptive technology was used to design the adaptive laws to approach the unknown parameters.Under certain conditions,the modified function projective synchronization could be realized between two non-identical chaotic systems.Then,in order to get the appropriate control input,the control gain was optimized.From view point of the effect of the synchronization,the controller was robust for the uncertainties of systems.Finally,the simulations verified the feasibility and effectiveness of the method.

chaotic systems;modified function projective synchronization;adaptive sliding mode control;robustness

TP391

A

1673-1522（2014）02-0101-04

10.7682/j.issn.1673-1522.2014.02.001

2013-12-20；

2014-02-24

余名哲（1982-），男，博士生；张友安（1963-），男，教授，博导，博士。