海杂波中广义符号恒虚警检测算法性能分析

刘卫华

（海军航空工程学院科研部，山东烟台264001）

在复杂的噪声背景下保持恒定的虚警概率是设计目标检测算法必须考虑的问题[1]。当杂波包络分布类型已知时，通过采集数据来估计某些参数，从而对信号进行有效的检测，这种检测方法被称为参量检测方法。然而，如果实际杂波分布和假设差距较大，检测性能就会大幅下降。因此，设计虚警概率与背景分布无关的检测算法很有必要，这种检测算法被称为非参量检测算法。在背景分布已知的情况下，非参量检测算法的性能往往不如参量检测算法，但是在背景分布未知的情况下，非参量检测算法的性能往往好于参量检测算法[2]。在雷达实际工作环境当中，杂波分布类型往往无法准确预知，因而非参量检测方法受到越来越广泛的关注[3-5]。常见的非参量检测算法有符号检测算法[6]，Wilcoxon检测算法[7]，广义符号（GS）检测算 法[2]和Mann-Whitney 检测算法[8]。GS 检测算法处理的是经包络检波器输出的回波信号，将检测单元与周围参考单元进行比较，并得到相应的非参量化检验统计量[7]，是易实现的两样本非参量检测算法之一。

为了研究GS检测算法对不同类型目标的检测性能，本文在仿真杂波数据、实测海杂波环境中，对GSCFAR检测算法的检测性能和海杂波抑制能力进行了仿真分析。由于GS检测算法的性能与脉冲数和参考单元数有关[2]，因而本文还研究了脉冲数和参考单元数对GS检测算法性能的影响。

1 算法模型

1.1 GS检测算法原理

GS 检测算法是对接收信号进行多脉冲检测的两样本符号检测算法。该算法将检测单元的幅度值与周围参考单元的幅度值进行比较，得到检测单元的检验统计量，再将检验统计量与对应的检测阈值比较。图1 给出了GS 检测算法的原理框图[7]，检测单元采样用yj(j=1,2,…,N) ，参考单元采样xji(i=1,2,…,M) 。检测单元两侧各有一个保护单元，防止检测单元中可能的目标信号泄漏到邻近的参考单元中而影响检测。

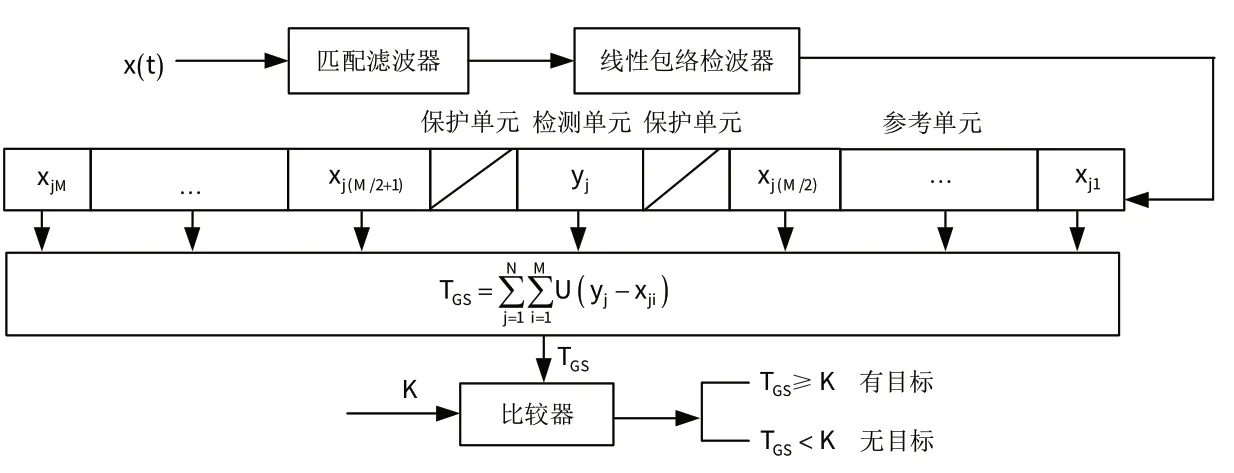
图1 GS检测算法原理框图Fig.1 Schematic diagram of GS detection algorithm

检验统计量

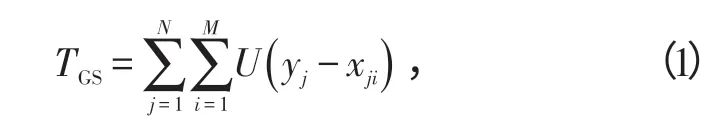
式中：U(⋅)是单位阶跃函数；N为脉冲数；M为参考单元数。

将检验统计量TGS和检测阈值K进行比较，如果TGS≥K，则判决存在目标；如果TGS＜K，则判决不存在目标。在无目标条件下，假设yj满足独立同分布；在有目标条件下，假设yj和xji满足独立同分布[2]。

1.2 检测阈值K 的确定

虚警概率Pfa可根据脉冲数N、参考单元数M和检测阈值K的大小来设定[2]，因而Pfa的值可以N、M和K进行函数表示，具体关系如式（2）所示：

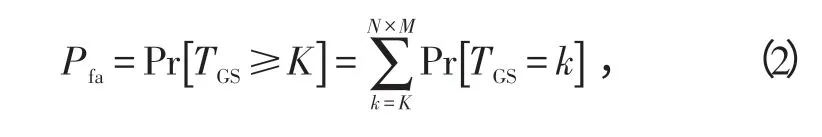
式中，

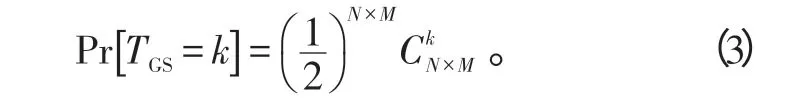
从式（2）可以看出，Pfa不依赖于杂波和噪声的分布形式，只与K、N和M有关，因而GS检测算法可使虚警概率保持恒定[7]。

当Pfa、N和M已知时，K可以由Pfa反解出来，那么K也不依赖于杂波和噪声的分布形式。当Pfa=10-4、N=10、M=16 时，根据上述公式得出K=127。

2 GS检测算法性能分析

2.1 仿真杂波+目标回波条件下的性能分析

本节采用高斯分布来模拟产生海杂波。分别产生I、Q2路标准高斯分布（均值为0，方差为1）序列，求包络后作为背景杂波数据。

产生不起伏Swerling 0 型目标回波和快起伏Swerling II型目标回波，将其与杂波数据合成，并调整信杂比（SCR）。

信杂比的计算公式为

当SCR已知时，可以根据上式反推出目标信号的幅度，从而计算出在不同信杂比情况下的检测概率[9]。

图2 给出了Pfa=10-3，脉冲数和参考单元数分别改变时，2种目标模型条件下，SCR与检测概率关系曲线。

图2 基于仿真数据的检测概率与信杂比关系曲线Fig.2 Relationship curve of detection probability and SNR based on simulated data

由图2可以看出：

1）当脉冲数和参考单元数一定，信杂比在一定范围内变化时，检测概率随着信杂比的增大而不断增大；

2）在信杂比和参考单元数一定的条件下，随着脉冲数的增大，检测概率有所增大；

3）在信杂比和脉冲数一定的条件下，随着参考单元数的增加，检测概率有所增大；

4）脉冲数变化对检测Swerling 0 型目标和Swerling II 型目标的影响要强于参考单元数对检测2 种目标的影响；

5）在低信杂比条件下，GS检测算法对Swerling II型目标的检测性能优于对Swerling 0型目标的检测性能；在高信杂比条件下，对Swerling 0型目标的检测性能优于对Swerling II型目标的检测性能。

2.2 真实杂波+仿真目标回波条件下的性能分析

为进一步验证不同参数对GS检测算法性能的影响情况，本节基于某实测数据对GS 检测算法性能进行分析，实际海杂波背景较为复杂，且分布类型一般是未知的。设Pfa=10-3，杂波数据是通过雷达采集得到的，目标类型仍采用Swerling 0 型和Swerling II 型。图3给出N和M分别变化时，2种目标模型的SCR与检测概率的对应关系曲线。

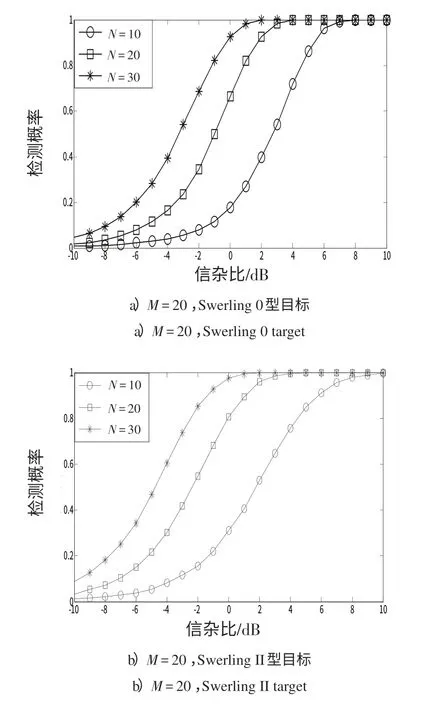
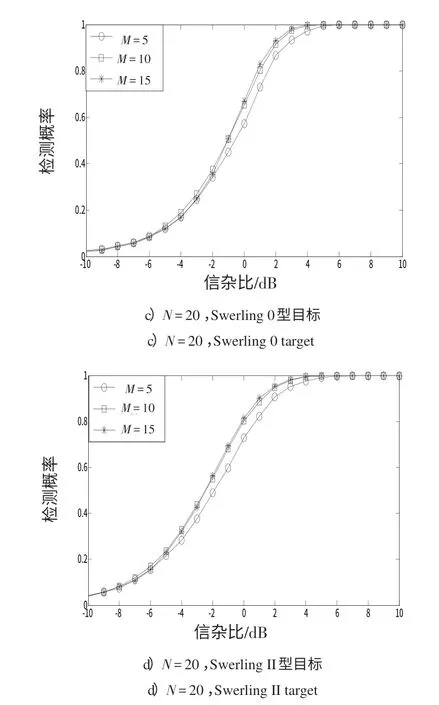
图3 基于实测数据的检测概率与信杂比关系曲线Fig.3 Relationship curve of detection probability and SNR based on real data

由图3可以看出：

1）在其他条件相同的情况下，检测概率随脉冲数的增大而有所增大。对于实测数据，在高信杂比条件下，对Swerling 0型目标的检测能力优于对Swerling II型目标的检测能力；在低信杂比条件下，对Swerling II型目标的检测能力优于对Swerling 0型目标的检测能力；

2）在其他条件相同的情况下，检测概率随着参考单元数的增大而有所增大，但变化不明显；

3）脉冲数变化对检测Swerling 0 型目标和Swerling II 型目标的影响要强于参考单元数对检测Swerling 0型目标和Swerling II型目标的影响。

上述分析进一步说明，GS 检测算法是一种与杂波分布类型无关的检测方法，即在不同的杂波分布类型情况下，几种参数对非参量检测算法性能的影响趋势保持一致。

分析原因：

1）Swerling II 型目标为快起伏目标，脉冲和脉冲间的起伏是统计独立的，若前一个脉冲没有超过门限，则相继脉冲有可能超过门限；而不起伏目标的相关性较强，如果第一个脉冲振幅小于检测门限，则相继脉冲也不会超过门限。在低信杂比条件下，信号幅度较低，快起伏目标经过检测算法处理之后得到的检验统计量超过检测阈值的概率相对较大而更容易被检测到；在高信杂比条件下，信号幅度相对较大，相对稳定的不起伏目标经过检测算法处理之后得到的检验统计量要高于快起伏目标，从而更容易被检测到；

2）GS 检测算法将检测单元和周围的参考单元进行比较以得到检验统计量，其本质是对目标优势的积累。若增大脉冲数，则在脉冲间相对稳定的有用信号的优势可得到进一步的积累，检测效果会明显改善。

2.3 真实杂波+真实目标回波条件下的性能分析

本节基于雷达对海上目标检测的实测数据进行分析，以验证GS 检测算法对渔船目标的检测性能。图4给出了虚警概率Pfa=10-3、脉冲数N和参考单元数M分别变化时的二维平面图。图4 中纵坐标表示距离单元，横坐标表示重复扫描的次数，每一个像素点表示一次扫描的回波强度[10]，图4 a）为原始数据平面图，图4 b）~d）为GS检测算法处理后的显示结果。

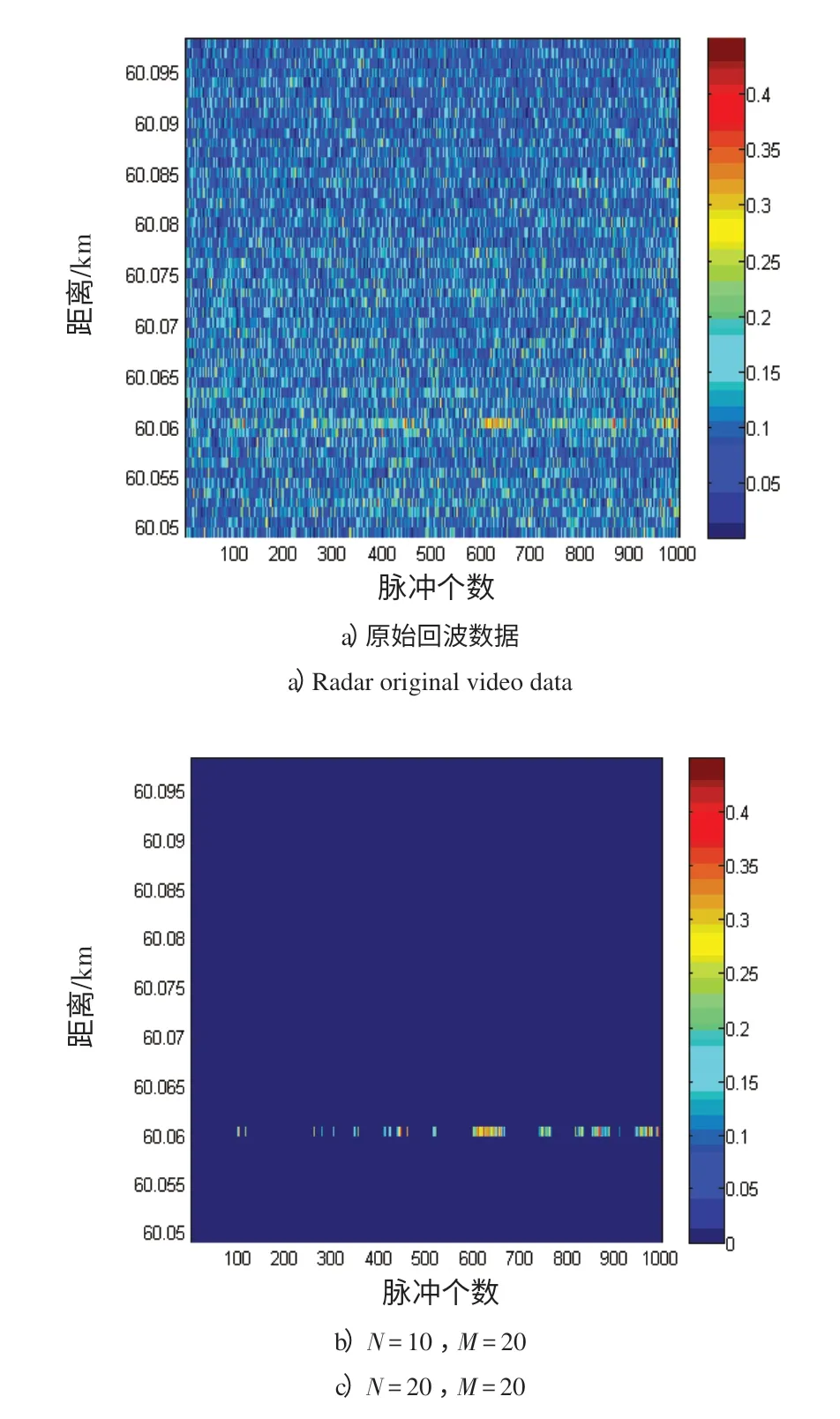
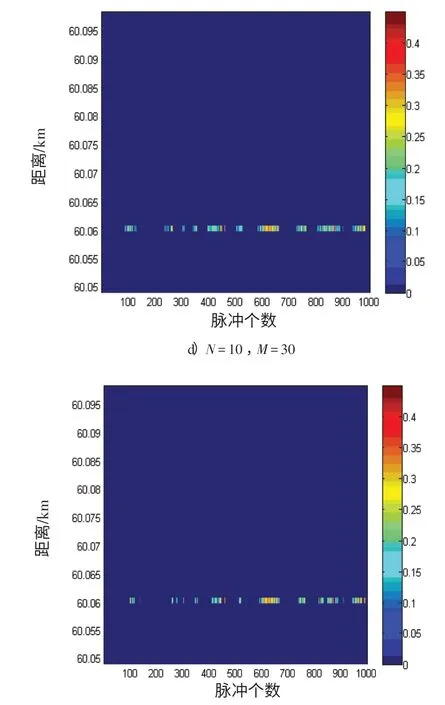
图4 实测数据显示图和检测算法处理结果Fig.4 Radar original video data and the result of detection algorithm

由图4 a）可知，在60 km处有1个渔船目标湮没在海杂波当中，较难分辨；经过GS检测检测算法处理后的结果如图4 b）~d）所示，绝大部分杂波被抑制掉，画面非常清晰。从图4可以看出：

1）相比于原始数据平面图，GS 检测算法成功检测出了目标，该检测算法对杂波有很好的抑制作用。当N增大时，颜色不一的间断条状回波逐渐变为连续的条状回波；

2）对于1 000 次观测，当M为20，N为10 时，检测到目标259 次；当M为20，N为20 时，检测到目标422次；当M为30，N为10时，检测到目标272次。由此可知，随着脉冲数N的增多检测效果明显变好，但参考单元数M对检测效果的影响并不明显。

3 总结

本文利用Swerling 0 和Swerling II 型目标回波叠加仿真杂波和实测海杂波数据，研究了不同参数，即信杂比、参考单元数和脉冲数对GS 检测算法性能的影响，并采用真实海杂波+目标回波数据进行验证。结果表明：

1）在高斯杂波背景和实测海杂波背景下，随着脉冲数、参考单元数和信杂比的增大检测概率不断增大，但脉冲数对检测概率的影响强于参考单元数对检测概率的影响；在高信杂比条件下，对Swerling 0型目标的检测能力优于对Swerling II 型目标的检测能力；在低信杂比条件下，对Swerling II 型目标的检测能力优于对Swerling 0型目标的检测能力。

2）通过对实测数据验证表明，GS 检测算法可以检测到海杂波中的渔船，在虚警概率保持不变的条件下，随着脉冲数和参考单元数的增大，算法的检测性能得到改善，但是参考单元数对检测性能的影响并不明显。

[1] 马克·理查滋.雷达信号处理基础[M].3 版.北京：电子工业出版社，2008：260-286.

MARK A RICHARDS. Fundamentals of radar signal processing[M]. 3rd ed. Beijing：Publishing House of Electronics Industry，2008：260-286.（in Chinese）

[2] VILHELM GREGERS HENSEN.Nonparametic radar extraction using a generalized sign test[J]. IEEE Transactions on Aerospace & Electronic Systems，1971，7（5）：941-950.

[3] SEYEF B，SHARAFAT A R. Signed-rank nonparametric multiuser detection in non-gaussian channels[J]. IEEE Transactions on Information Theory，2005，51（4）：1478-1486.

[4] HAO CHEN. Noise enhanced nonpatametric detection[J].IEEE Transactions on Information Theory，2009，55（2）：499-506.

[5] ORTON M.Nonparametric rank detectors under k-distributed clutter in radar application[J]. IEEE Transactions on Aerospace&Electronic Systems，2005，41（2）：702-710.

[6] CARLYLE J W. On nonparametric siganl detectors[J].IEEE Transactions on Information Theory，1964，10（2）：146-152.

[7] 何友，关键. 雷达目标检测与恒虚警处理[M]. 2 版. 北京：清华大学出版社，2011：230-250.

HE YOU，GUAN JIAN. Radar target detection and cfar processing[M]. 2rd ed. Beijing：Tsinghua University Press，2011：230-250.（in Chinese）

[8] ZEORI G W. Performance of a two-sample mann-whitney nonparametric detector in a radar application[J].IEEE Transactions on Aerospace & Electronic Systems，1971，7（5）：951-959.

[9] 赵志坚.海杂波中非参量恒虚警检测算法性能分析[J].雷达科学与技术，2010，8（1）：65-73.

ZHAO ZHIJIAN. Performance analysis of nonparametric CFAR detectors in sea clutter[J].Radar Science and Technology，2010，8（1）：65-73.（in Chinese）

[10] 张林. 三种两样本非参量检测器CFAR 检测算法分析[J].海军航空工程学院学报，2011，26（3）：296-300.

ZHANG LIN.Performance analysis of three kinds of twosample nonparametric CFAR detectors[J]. Journal of Navel Aeronautical and Astronautical University，2011，26（3）：296-300.（in Chinese）