一种适用于任意阵列的极化和二维DOA联合估计算法

郑均杰，刘国峰，王晓东

（92785部队，河北秦皇岛066200）

极化敏感阵列不仅能够获取信号的空间到达角信息，而且可以获取信号本身所具有的极化信息。因此，相比于标量传感阵列，极化敏感阵列有许多独特的性能优势[1-2]。比如说较强的抗干扰能力、稳健的检测性能、极化多址和较高的系统分辨率等。鉴于极化敏感阵列的优势，极化敏感阵列信号处理成为了阵列信号处理领域中的研究热点。同样，极化敏感阵列在民用和军事上有着广泛的应用。比如在移动通信系统中，利用极化敏感阵列可以进一步克服多径衰落干扰和共信道干扰等。在军事上，利用极化敏感天线阵列可以提高机载雷达抑制地杂波能力和地基雷达抗干扰能力等[2]。

有关阵列信号极化和二维DOA 参数联合问题，国内外学者已做了一定的相关工作。比如，文献[3-5]基于均匀网格的平面阵应用ESPRIT的方法可以估计出二维角度和极化信息。文献[6]提出了可以适用于任意阵列结构的二维求根DOA 和极化联合估计算法，文献[7]基于圆柱阵列提出的迭代ESPRIT 的方法估计二维角度和极化信息等。空时二维处理是在进行空域处理的同时引入了对时域信息处理，充分利用了信号有用信息，可以降低对阵列结构的约束，提高抗噪能力[8-9]。本文提出了基于时空处理的极化和二维DOA联合估计算法并进行了论证和仿真。

1 阵列结构与数据模型

对于任意几何结构的N元阵列，第n个阵元的坐标为(pnx,pny,pnz)。选择不在同一条直线的3 个阵元p0、p1、p2和作为导引阵元，设p0位于坐标原点，阵列结构如图1 所示，图中pn( 0≤n≤N-1) 表示第n个阵元的位置矢量。用ex表示x轴的单位矢量，ey表示y轴的单位矢量，ez表示z轴的单位矢量，pn与ex、ey和ez的关系为：

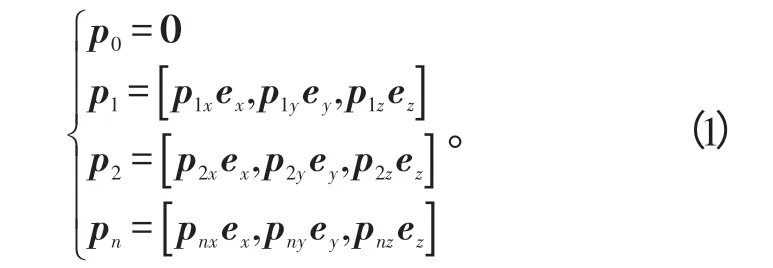
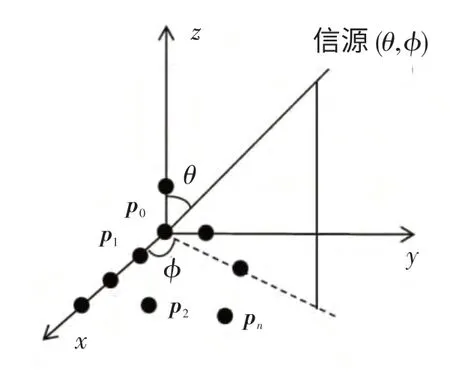
图1 阵列模型Fig.1 Array model

假设有K个已知载频为ω0，波长为λ的不相关窄带信号源s1(t),s2(t),…,sK(t)入射到阵列，其入射角分别为 (θ1,ϕ1),(θ2,ϕ2),…,(θK,ϕK) ，极化状态为。为了避免多值，这里0 ≤γk≤π/2；0 ≤ηk≤2π(1 ≤k≤K) 。设每个阵元的极化辐射方向图相同。

则第n个阵元的输出为：

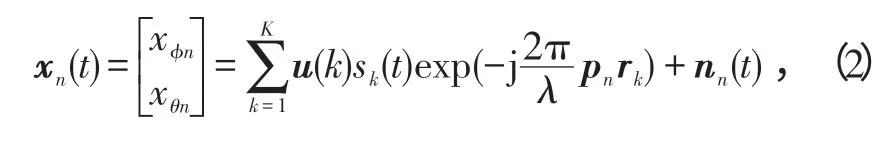
式中：n=0,1,…,N-1；u为考虑信号极化状态后的ϕ和θ方向的极化系数矢量，且

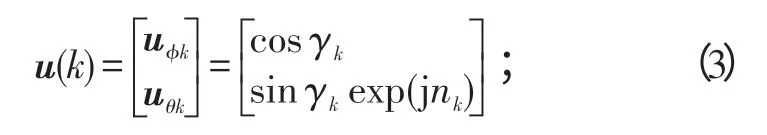
sk(t)为第k个入射信号，sk(t)= ||Ekexp(j(ω0t+Ψk))， ||Ek为幅度，Ψk为[0,2π]内均匀分布的初始相位；rk为第k个信号的传播矢量，且

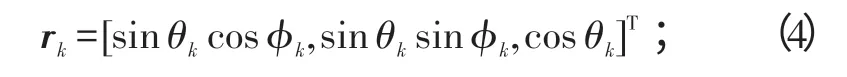
nn(t)为加性噪声矢量，其均值为零，且各阵元间互不相关。

2 极化和二维DOA联合估计

2.1 时空估计矩阵构造

p0、p1、p2为已经校准阵元，令其作为导引阵元。

定义阵元p0与各阵元的相关函数为：

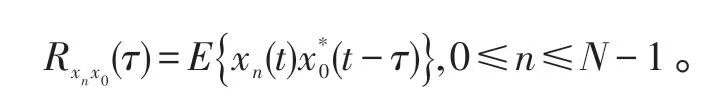
定义阵元p1与各阵元的相关函数为：

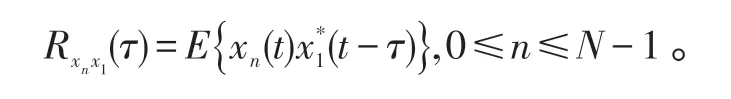
定义阵元p2与各阵元的相关函数为：

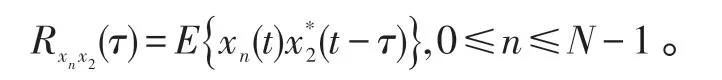
由式（2）可知：

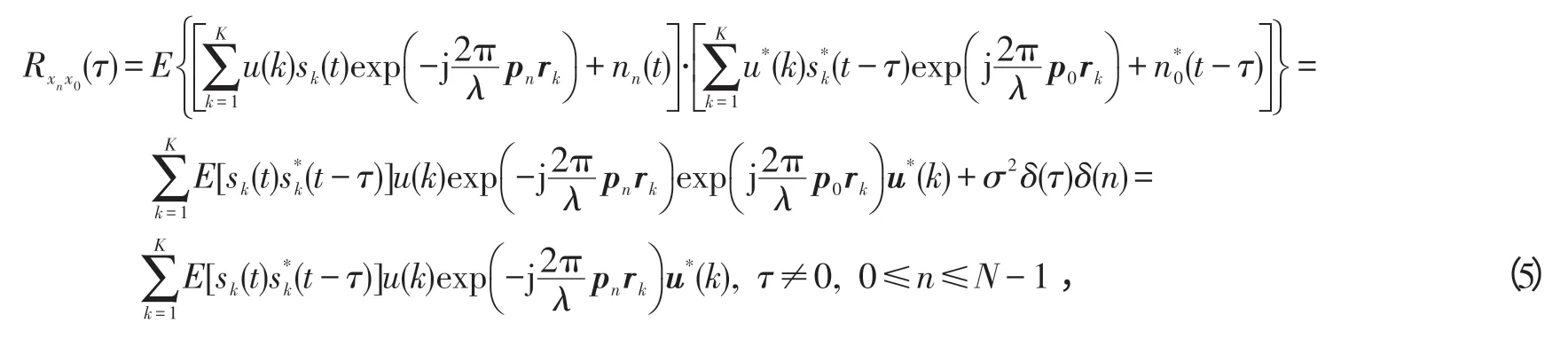
[9]中的方法构造如下时空矩阵：

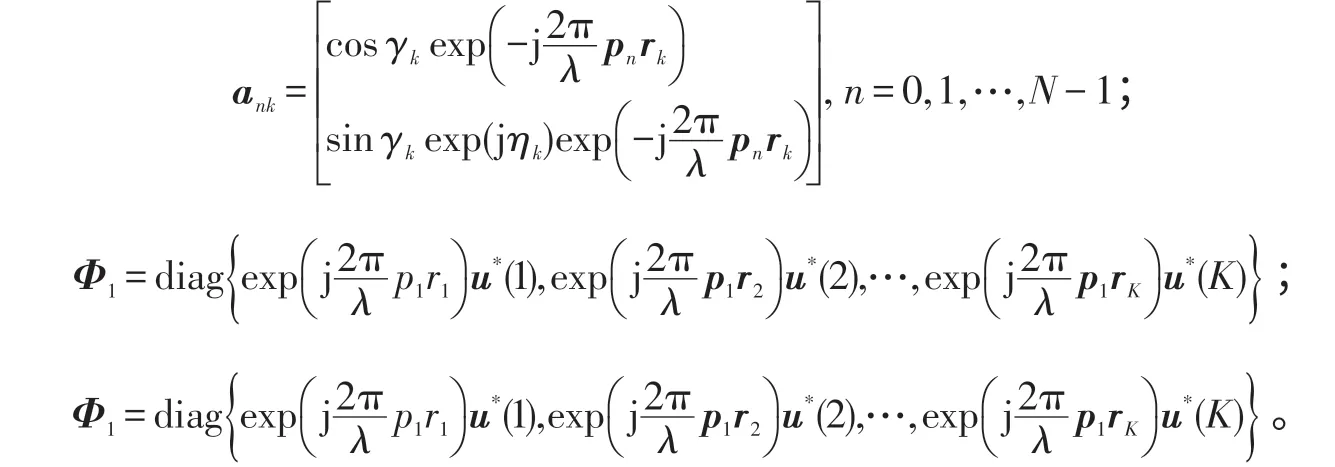
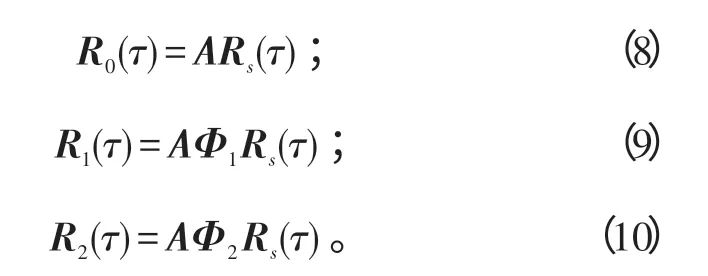
其中，diag{}· 表示对角矩阵，则式（5）~（7）的矩阵形式为：式（8）~（10）具有类似结构，类似于对阵列输出做快拍采样，对R0(τ)、R1(τ) 和R2(τ) 以时间延迟τs(τs=Ts,2Ts,…,NT,Ts需要小于2π/ω0s) 为单位进行M(M≥K)次采样，得到2N×M维的“伪快拍矩阵”：

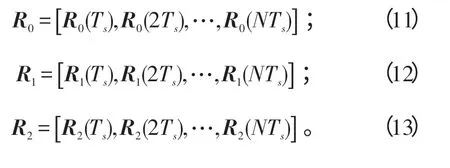
式（11）~（13）可以分别写成：

式（14）～（16）中，S=[]Rs(Ts),Rs(2Ts),…,Rs(NTs) 。分别对“伪快拍矩阵”求自相关和互相关矩阵为：式（17）～（19）中，RSS为S的自相关矩阵。

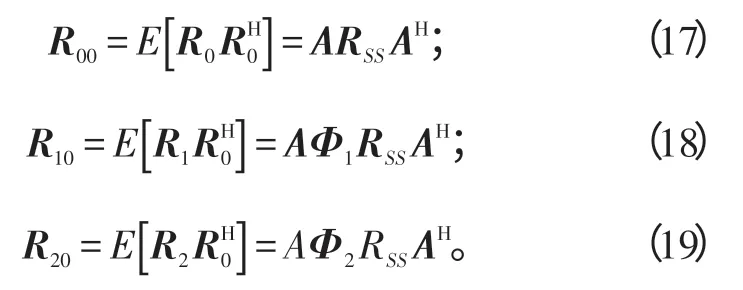
参考DOA矩阵方法[9]，定义“时空估计矩阵”为：

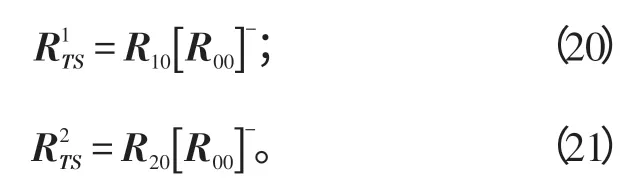
定理1：如果A与RSS满秩，Φ无相同的对角元素，则时空估计矩阵的K个非零特征值等于Φ中K个对角元素，而这些值对应的特征向量等于相应的信号导向矢量，即RA=AΦ。

其证明见文献[10]。观察和不是满秩的。但其奇数行和偶数行分别构成等价的满秩矩阵。因此，对时空估计矩阵进行特征分解同样可以得到A和Φ1，对的特分解可以得到A和Φ2。

此时，

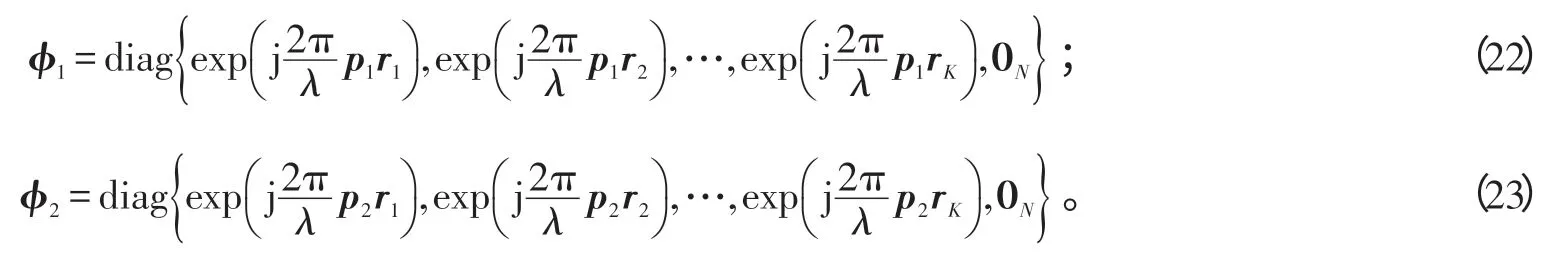
式（22）、（23）中，0N表示1×N的零矩阵。

2.2 参数配准

由于Φ1和Φ2是2 次独立的特征分解得到的,其特征值与特征向量的排列次序是随机的。因此，需要对2 次分解的参数进行配准[9]。将特征分解得到的A记为A1，特征分解得到的A记为A2。因为特征值与特征向量存在对应关系，所以A1与A2只是在列向量的排列次序上存在差异，即

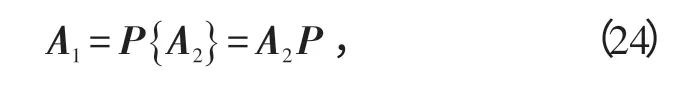
式中，{P}· 为置换算子，由K×K维置换矩阵P实现。

P的任意一行或一列中有且只有一个元素为1，其余元素为0。由于Φ中的对角元素与A中的列向量存在固定的对应关系，因而可以将算子P作用于A2，使它的列向量与A1的列向量对齐，类似地将相同的操作作用于Φ2：

这样，使得Φ′2与Φ1的对角元素配准，且由式（24）可得到

在得到了对齐的Φ1和Φ′2后，由式（22）、（23）有：

由于3 个导引阵元不在一条直线上，可以从上式中唯一地解出θk和ϕk。为了保证不出现角度的周期性模糊，3个导引阵元的间距不能超过半波长[11]。

A的偶数行和奇数行分别是信号θ和ϕ方向的信号导向矢量，定义[12]：

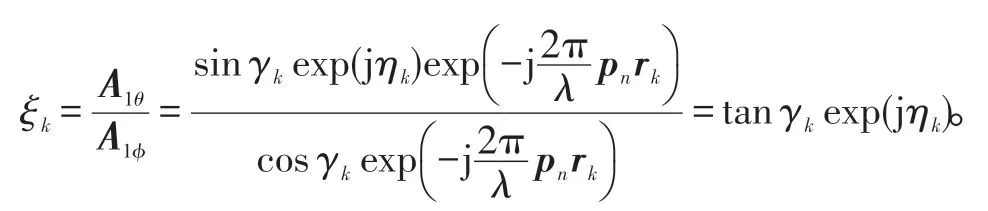
这样取任意阵元的θ和φ方向的信号导向矢量比，得到ξk，则有：

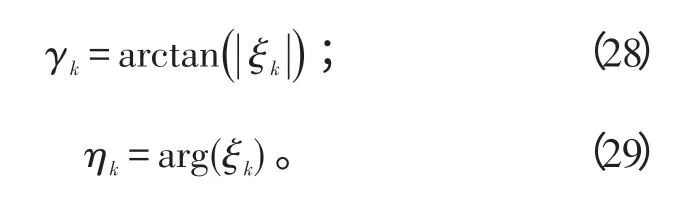
3 仿真实验

实验1：采用图2的6元阵，坐标分别为p0(0,0,0)，p1(λ/4,0,0) ，p2(λ,λ,0) ，p3(0,λ/4,0) ，p4(0,λ,λ) ，p5(0,0,λ/2)。设各阵元辐射方向图相同且为全向，令p0、p1、p3做导引阵元。

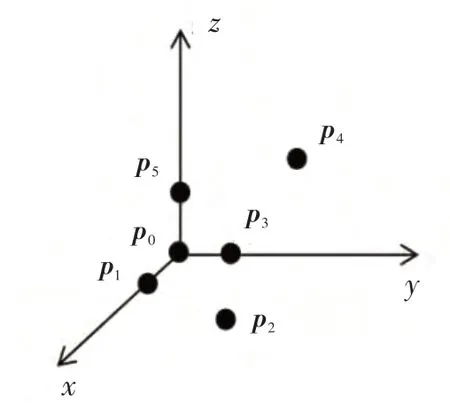
图2 阵列结构Fig.2 Array structure

有2 个互不相关窄带信号源入射，其极化与二维波达角参数对(θk,ϕk,γk,ηk)，分别为(30°,30°,45°,5°)和(70°,40°,50°,10°)，采用200次快拍和100次伪快拍，信噪比为20 dB，进行500 次独立的Monte-Carlo 实验。图3和图4分别给出了二维波达角与极化特性的估计结果。

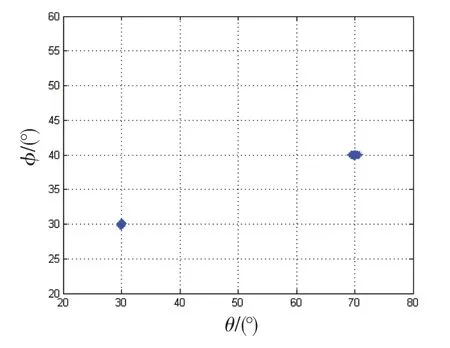
图3 二维波达角估计结果Fig.3 Results of 2D DOA estimation

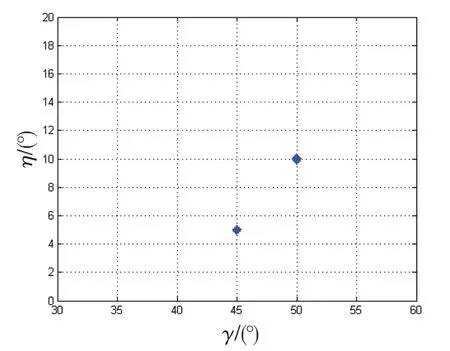
图4 极化特性估计结果Fig.4 Estimation results of polarization characteristics

从图3 和图4 可以看出，本文提出的算法可以利用较少的采样数据正确地估计出信源的二维波达角与极化特性，其适用于任意阵列。唯一要求是3 个导引阵元间隔不能超过半个波长。

实验2：阵列与信源设置同实验1，采用200 次快拍和100次伪快拍，进行500次独立实验，图5给出了2个信源二维波达角估计的最小均方根误差（RMSE）随信噪比的变化曲线，图6 给出了信源极化特性估计的最小均方根误差（RMSE）随信噪比的变化曲线。

定义信源k的二维波达角估计的均方根误差为

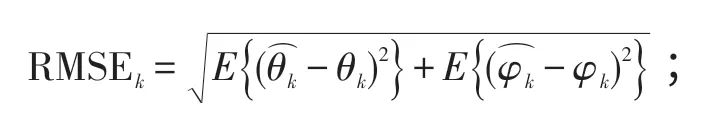
定义信源k的极化特性估计的均方根误差为

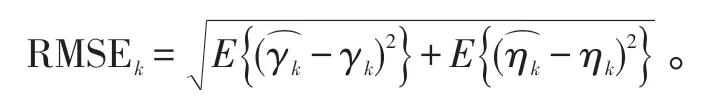
由图5和图6可以看出，随着SNR的增加，算法估计的均方根误差逐渐减小，估计的精度逐渐高，说明了算法的有效性。

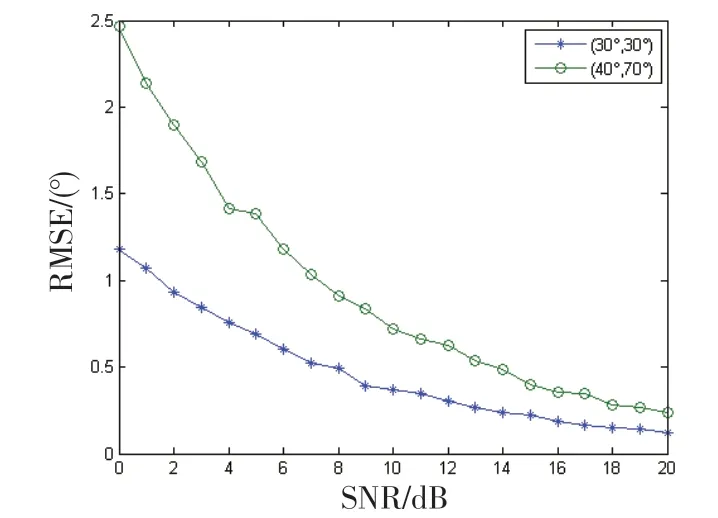
图5 二维波达角估计结果的RMSE随SNR变化曲线Fig.5 Estimate results the 2D DOA of RMSE changed with SNR

4 结束语

本文提出了基于信号时空特征结构的二维DOA和极化联合估计算法。该算法通过阵元间的互相关函数将空域的阵列数据变换到时空域，利用时空域上的伪快拍数据矩阵构造时空估计矩阵。通过时空估计矩阵特征分解得到的特征值和特征矢量可以同时估计出信源的波达方向和极化特性，无须谱峰搜索，参数配对算法简单，计算量较小。在满足3 个导引阵元间距不超过半个波长条件时，该算法适用于任意阵列。仿真实验验证了算法的有效性。

参考文献：

[1] 杨鹏.基于复杂载体的共形软件天线关键技术研究[D].成都：成都电子科技大学，2012.

YANG PENG.Study of key techniques of conformal software antenna based on complex platforms[D]. Chengdu：Chengdu University of Electronic Science and Technology，2012.（in Chinese）

[2] 许凌云.阵列多参数联合估计算法及应用的研究[D].南京：南京航空航天大学，2011.

XU LINGYUN.Array multi-parameter joint estimation algorithm and its application research[D]. Nanjin：Nanjing University of Aeronautics and Astronautics，2011.（in Chinese）

[3] LI J，COMPTON R T.Angle and polarization estimation using ESPRIT with a polarization sensitive array[J].IEEE Transactions on Antennas Propagate，1991，39（9）：1376-1383.

[4] LI J. Direction and polarization estimation using arrays with small loops and short dipoles[J]. IEEE Transactions Antennas Propagate，1993，41（3）：379-387.

[5] LI J，COMPTON R T. Two dimensional angle and polarization estimation using the ESPRIT algorithm[C]//Antennas and Propagation Society International Symposium.1991：388-391.

[6] COSTA M A，RICHTER A，KOIVENEN V.Azimuth，elevation and polarization estimation for arbitrary polarimetic array configurations[C]//IEEE workshop on statistical signal process.2009：261-264.

[7] 邹麟.基于几何代数的共形阵列空域信号处理研究[D].成都：成都电子科技大学，2012.

ZOU LIN. Research on array spatial signal processing based on conformal geometric algebra[D]. Chengdu：Chengdu University of Electronic Science and Technology，2012.（in Chinese）

[8] 孙晓颖，陈建，林琳.基于时空处理的频率与二维DOA联合估计算法[J].通信学报，2009，30（8）：39-44．

SUN XIAOYING，CHEN JIAN，LIN LIN. Joint signal carrier frequency and 2D DOA estimation method based on space-time processing[J]. Journal on Communicatins，2009，30（8）：39-44.（in Chinese）

[9] 金梁，殷勤业.时空DOA 矩阵法[J].电子学报，2000，28（6）：8-12．

JIN LIANG，YIN QINYE. Space-time DOA matrix method[J].Acta Eletronica Sinica，2000，28（6）：8-12.（in Chinese）

[10]殷勤业.高分辨率波达方向估计[D].西安：西安电子科技大学，1989.

YIN QINYE. High resolution DOA estimation[D]. Xi'an：Xidian University，1989.（in Chinese）

[11] GODRICH H，HAIMOVICH A M，BLUM R S.Targetlocalization accuracy gain in MIMO radar-based systems[J]. IEEE Transactions on Information Theory，2010，56（6）：2783-2803.

[12]TAJER A，JAJAMOVICH G H，WANG X，et al. Optimal jointtarget detection and parameter estimation by MIMO radar[J]. IEEE Journal of Selected Topics in Signal Processing，2010，4（1）：127-145.