CNS/SINS姿态组合导航系统仿真

（海军航空工程学院电子信息工程系，山东烟台264000）

惯性导航系统（Inertial Navigation System，INS）以其短时精度高，可以连续地输出位置、速度、姿态信息，以及完全自主等突出优点，已被各种类型的军用飞行器普遍采用[1-5]。由于陀螺等惯性测量单元（Inertial Measurement Unit，IMU）的漂移或误差使导航输出误差随时间积累难以长时间独立工作，因而需要增加其他外部量测信息，利用组合的方法提高综合导航性能。

天文导航系统（Celestial Navigation System，CNS）主要特点有：被动探测、隐蔽性好、不受电磁干扰、可靠性高、自主工作、不依赖其他导航手段、精度高、在惯性坐标系下，测量误差也不随时间而积累。其中，定向精度最高，而定位精度也仅次于全球定位系统（Global Positioning System，GPS），可全天候工作。天文导航作为一种隐蔽、无源、被动的导航手段，不存在无线电导航系统在恶劣战场电磁环境条件下易受到干扰的问题，在战时将具有极高的军事应用价值[6]。采用CNS/INS组合克服了各自缺点，取长补短，构成了一种比较理想的组合导航系统。

目前，CNS/INS组合导航系统有多种工作模式，根据星敏感器和惯性器件安装方式的不同，可分为全平台式、平台惯性导航系统与捷联星敏感器模式、捷联惯性导航系统与平台星敏感器模式以及全捷联模式4种[7]。由于制造成本、可靠性、测量精度、未来发展趋势等因素，全捷联模式的天文/惯性组合导航系统更有发展前景，是天文/惯性组合导航系统的重要发展方向之一，为此本文的以下内容都将以全捷联模式为例。

星敏感器测量输出的惯性系下姿态信息，在其转换为地理系下的载体姿态信息之前，无法直接应用于实际的地理坐标系导航。

本文对地理系下姿态观测原理进行了充分阐述，分析并建立了地理系下姿态线性化量测方程及状态方程。

1 天文/惯性姿态组合导航算法研究

1.1 地理系下姿态观测原理

天文/惯性组合导航系统比纯惯导系统的精度高是因为在惯性空间里恒星的方位基本保持不变，尽管星敏感器的像差、地球极轴的进动和章动以及视差等因素使恒星方向有微小的变化，但是它们所造成的资态误差小于1″，因而星敏感器就相当于没有漂移的陀螺，所以可以用天文量测信息修正惯性器件误差[8]。但是，现在大部分导航平台使用地理坐标系进行导航，天文导航在地理坐标系下姿态解算依赖导航位置而容易发生精度发散，为此需要研究地理坐标系下天文/惯性姿态组合导航系统，来提高导航精度。

由于惯性组合导航系统中与姿态误差相关的状态误差通常选择为平台误差角(φE,φN,φU)，但其并不等同于姿态误差角。为实现姿态误差观测量到平台误差角之间的转换，目前有2种主要方法：一种是采用近似的方式，将姿态误差和平台误差看为等价关系；另一种则是将姿态测量误差转换为平台误差角，然后再进行组合滤波。但就这2种方法本质而言，均具有其不足之处：如第1种方法具有建模的近似性，会带来相应的建模误差；而第2种方法将姿态误差测量转换为平台误差角测量，也会带来相应的转换误差。

由以上原因，本文为克服上述2种姿态组合算法的不足，进一步提高组合系统精度，采用直接建立姿态误差观测量和系统状态量之间的线性化量测方程的方法。

在全捷联工作模式下，由星敏感器输出的姿态信息可以得到载体的三轴姿态信息（俯仰角θS、航向角ψS、滚转角γS），而惯性导航系统通过惯导解算也会给出载体的三轴姿态信息（俯仰角θI、航向角ψI、滚转角γI）,因此，将两者相减可得到载体的三轴姿态误差角Δε为式（1）。为直接获得线性化的姿态观测方程，做如下理论推导：

1.1.1 姿态观测关系分析

式（2）是根据姿态角度定义，导航坐标系下的理想姿态转换矩阵[9]，上标n表示导航坐标系，下标b表示载体本体坐标系；γ、θ、ψ分别表示载体相对于地理系下的滚动、俯仰和航向理想姿态信息。定义由惯性导航模拟的导航平台坐标系东向、北向和方位平台误差角分别为φE、φN、φU。则利用惯性导航计算输出姿态和平台误差角，也可以获得相对于导航坐标系下的理想姿态转换矩阵：

式（3）中，上标c1表示通过惯性导航计算获得的导航平台坐标系。由式（2）和式（3）可以获得上面计算等式（4）。式（4）反映了惯性导航计算输出姿态角、平台误差角和理想姿态之间的相互关系，可以利用上述等式关系获得组合观测量Δγ、Δθ、Δψ的计算表达式。但由于其为非线性方程，而为采用线性卡尔曼滤波器，还必须直接获得组合系统的线性化量测方程，则必须利用上述关系求解出组合观测量Δγ、Δθ、Δψ，并建立其和状态量之间的线性量测关系。

1.1.2 角度观测方程建立

利用在小角度姿态偏差情况下，Δγ、Δθ、Δψ为小量的假设以及三角函数关系，则有：

此外，对式（3）中的Cc1b可做如下简化表达：

由式（6）和（4）化简得式（7）。利用式（7）中矩阵对应元素相等的关系，即可获得姿态角度观测量Δγ、Δθ、Δψ。式（7）中部分元素与计算无关，用“…”表示。由前文提到的，星敏感器提供的姿态信息误差非常小，可近似为载体的姿态，则有如下的矩阵元素对应关系式（8）。将式（5）代入式（8），经过简化，可以获得最终的姿态角度线性化量测方程为式（9）：

1.2 系统状态方程

采用线性卡尔曼滤波器进行组合，系统的状态方程为惯性导航系统的误差方程，通过对惯性导航系统的性能及误差源的分析获得惯导系统的误差方程为：

式中系统状态变量定义参考文献[9-10]。可对上述连续形式的系统状态方程和量测方程进行离散化处理，采用线性离散卡尔曼滤波器进行滤波估计[9]。

1.3 IMU输出信息的仿真模型

载体飞行轨迹发生器作为组合导航仿真系统研究的基础[11-14]，用来产生IMU 在地理坐标系下的原始输出。本文根据设定的轨迹信息（初始位置、速度和姿态及不同时段内速度和姿态变化率），由轨迹方程得到地理坐标系下的位置、速度、姿态；在地理坐标系下，根据运动学关系反推到IMU输出的比力和角速率信息。而实际中惯性器件的输出总是存在误差的，IMU 误差主要包括随机误差和固定误差。陀螺与加速度计的随机误差均包括白噪声、一阶马尔科夫过程随机噪声误差、等效常值漂移误差；陀螺的固定误差包括：陀螺标度因数误差，陀螺安装误差。加速度计的固定误差包括：加速度计标度因数误差，加速度计安装误差，加速度计二次项系数误差[2，14]。

本文仿真中，卡尔曼滤波算法采用间接法反馈校正滤波器结构，算法递推公式参考文献[9，10，15]。建立仿真流程框图如图1所示。

图1 天文/惯性姿态组合导航仿真流程图Fig.1 Simulation flow chart of CNS/SINS posture integrated navigation

在本文的仿真流程图中的各模块功能：

1）航迹解算模块输出载体在载体坐标系下，随时间变化的姿态、速度、加速度。

2）SINS 数据解算模块根据给定的IMU 误差和航迹信息，算出地理坐标系下的载体位置、速度和姿态。

3）天文姿态的计算利用了惯导给出的位置与航迹解算出的位置、姿态信息。

考虑到由格林尼治恒星时角GAST可获得惯性坐标系到地球固联坐标系的变换矩阵为Cei；再利用惯导提供的地理经纬度信息，可获得地球固联坐标系到导航坐标系的变换矩阵Cen。其中，Cie和Cen的计算公式如式（11）和（12）所示：

式（11）中，下标i表示惯性坐标系，上标e表示地球固连坐标系。则有载机相对于导航坐标系的姿态变换矩阵：

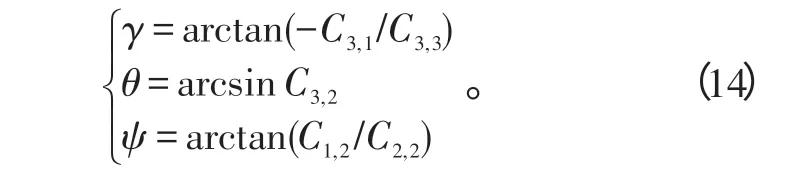
上式即机体系相对于导航系的3个姿态角，其中Ci,j表示矩阵中下标为(i,j)的元素。

4）卡尔曼滤波反馈不但能够调整IMU的误差修正值，还能修正导航输出的位置，速度和姿态信息。

2 天文/惯性姿态组合导航系统仿真

2.1 仿真条件设置

假设飞机做机动飞行，其飞行航迹如图2所示，含爬升、变速、平飞和转弯等各种飞行状态。仿真过程中惯导系统的采样周期为0.02 s；CNS 数据采样周期为1 s；Kalman滤波信息融合周期为1 s。惯导系数误差参数见表1所示。

图2 仿真飞行航迹Fig.2 Simulation flying track

表1 惯导误差参数Tab.1 Error parameters of SINS

2.2 仿真结果与分析

对相同的航迹、惯导误差仿真数据，本文进行了纯惯导和天文/惯性组合导航的仿真，其中图3～5分别给出了纯惯导与天文/惯性导航的位置误差、速度误差、姿态误差的比较。图中，SINS 所指曲线为纯惯导误差曲线；CNS/SINS 所指曲线为天文/惯性组合导航误差曲线。

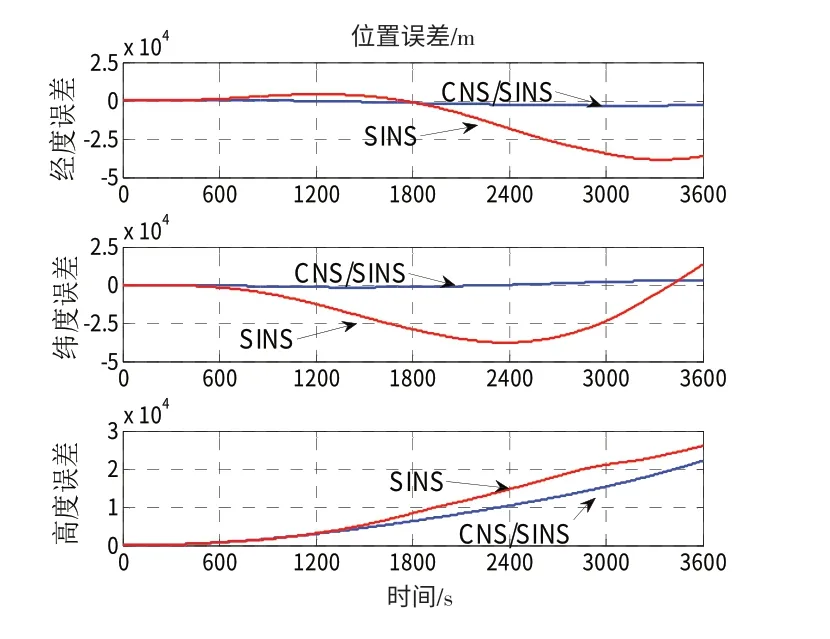
图3 纯惯导与天文/惯性组合导航位置误差比较Fig.3 Comparison of position error between SINS with CNS/SINS

图4 纯惯导与天文/惯性组合导航速度误差比较Fig.4 Comparison of velocity error between SINS with CNS/SINS

图5 纯惯导与天文/惯性组合导航姿态误差比较Fig.5 Comparison of posture error between SINS with CNS/SINS

从仿真结果可以得出如下结论：

1）纯惯导与天文/惯性组合导航在导航的初始阶段，误差都比较低。由于IMU的漂移和误差随时间积累，纯惯导的精度发散比较快，而组合导航比较缓慢，证实了天文/惯性姿态组合导航的效果。

2）当惯导与天文导航进行姿态组合后在短期内可认为是收敛的，但当仿真时间较长后，各导航参数呈现出非常慢的发散趋势，原因是CNS的姿态的解算依赖于导航的位置。

3）经过CNS 与SINS组合后，各导航参数都得到了明显提高，但高度通道改善的效果有待提高。

4）滤波器能有效估计陀螺及加速度计各项误差。

3 结论

本文首先在分析CNS/SINS组合导航系统的基础上建立了系统各模块的数学模型，并基于Matlab软件开发出仿真系统。该系统能够实现设定轨迹的IMU和CNS数据的仿真，并且利用原始数据进行姿态组合导航运算，本文的仿真结果验证了该仿真系统的实用性；然后，介绍了CNS/SINS 姿态组合系统的融合算法；最后，根据滤波实际设定组合导航系统各项参数并获得仿真数据。

纯惯导与天文/惯性组合导航在导航的初始阶段，误差都比较低。由于IMU的漂移和误差随时间积累，纯惯导的精度发散比较快，而组合导航比较缓慢，证实了天文/惯性姿态组合导航的效果。经过CNS 与SINS组合后，位置精度、速度精度与姿态精度都得到了明显提高，但改变不了其发散的趋势，原因是CNS的姿态的解算依赖于导航的位置；同时，高度通道改善的效果有待提高。为了进一步提高位置及速度的滤波精度，可研究精度更高的量测方程，或加入GPS参与组合。

[1]曾伟，林训超，曾友州，等.组合导航技术的发展趋势[J].成都航空职业技术学报，2011，27（2）：41-44.

ZENG WEI，LIN XUNCHAO，ZENG YOUZHOU，et al.The development tendency of the integrated navigation technology[J].Chengdu Aeronautical Vocational and Technical Journals，2011，27（2）：41-44.（in Chinese）

[2]张光天，王秀萍，王丽霞.捷联惯性导航技术[M].北京：国防工业出版社，2010：9-10，106-109.

ZHANG GUANGTIAN，WANG XIUPING，WANG LIXIA.Strapdown inertial navigation technology[M].Beijing：National Defence Industry Press，2010：9-10，106-109.（in Chinese）

[3]PHILIPS CRAIG A.Guidance algorithm for range maximization and time-of-flight control of guided projectile[J].Journal of Guidance，Control，and Dynamics，2008，31（5）：1447.

[4]曹岩，赵家胜，王伟，等.弹载捷联惯性导航系统算法及仿真[J].西安工业大学学报，2011，31（3）：231-235.

CAO YAN，ZHAO JIASHENG，WANG WEI，et al.Algorithm for strapdown inertial navigation system and its simulation[J].Journal of Xi'an Technological University，2011，31（3）：231-235.（in Chinese）

[5]刘莉娜，刘任庆.基于捷联惯性导航的组合导航系统研究[J].现代电子技术，2009（3）：111-113.

LIU LINA，LIU RENQING.Reserch of integrated navigation system based on strapdown inertial navigation system[J].Modern Electronics Technique，2009（3）：111-113.（in Chinese）

[6]张宗麟.惯性导航与组合导航[M].北京：航空工业出版社，2000：20-24.

ZHANG ZONGLIN.Inertial navigation and integrated navigation[M].Beijing：Aviation Industry Press，2000：20-24.（in Chinese）

[7]全伟，刘百奇，宫晓琳，等.惯性/天文/卫星组合导航技术[M].北京：国防工业出版社，2011：177-179.

QUAN WEI，LIU BAIQI，GONG XIAOLIN，et al.INS/CNS/GPS integrated navigation technique[M].Beijing：National Defense Industry Press，2011：177-179.（in Chinese）

[8]房建成，宁晓琳.天文导航原理及应用[M].北京：北京航空航天大学出版社，2006：266-267.

FANG JIANCHENG，NING XIAOLIN.The principle and application of the celestial navigation[M].Beijing：Beihang University Press，2006：266-267.（in Chinese）

[9]袁信，俞济祥，陈哲.导航系统[M].北京：航空工业出版社，1993：137-140.

YUAN XIN，YU JIXIANG，CHEN ZHE.Navigation system[M].Beijing：Aviation Industry Press，1993：137-140.（in Chinese）

[10]秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社，1998：33-56.

QIN YONGYUAN，ZHANG HONGYUE，WANG SHUHUA.Kalman filter and the principle of the integrated navigation[M].Xi’an：Northwestern Polytechnical University Press，1998：33-56.（in Chinese）

[11]卞鸿巍，李安，谭方君，等.现代信息融合技术在导航中的应用[M].北京：国防工业出版社，2010：97-100.

BIAN HONGWEI，LI AN，TAN FANGJUN，et al.The application of modern information fusion technique in navigation[M].Beijing：National Defense Industry Press，2010：97-100.（in Chinese）

[12]赖际舟，于永军，熊智，等.惯性/天文深组合非线性定位算法[J].控制与决策，2012，27（11）：1649-1652.

LAI JIZHOU，YU YONGJUN，XIONG ZHI，et al.SINS/CNS tightly integrated navigation positioning algorithm with nonlinear filter[J].Control and Decision，2012，27（11）：1649-1652.（in Chinese）

[13]屈蔷，刘建业，熊智，等.机载天文/惯性位置组合导航[J].南京理工大学学报：自然科学版，2010，34（6）：729-732.

QU QIANG，LIU JIANYE，XIONG ZHI，et al.Airborne SINS/CNS location integrated system[J].Journal of Nanjing University of Science and Technology：Natural Science，2010，34（6）：729-732.（in Chinese）

[14]宁晓琳，蔡洪炜，吴伟仁，等.月球车的惯性/天文组合导航新方法[J].系统工程与电子技术，2011，33（8）：1837-1844.

NING XIAOLIN，CAI HONGWEI，WU WEIREN，et al.INS/CNS integrated navigation method for lunar rover[J].System Engineering and Electronics，2011，33（8）：1837-1844.（in Chinese）

[15]熊智，刘建业，郁丰，等.基于天文角度观测的机载惯性/天文组合滤波算法研究[J].宇航学报，2010，31（2）：397-403.

XIONG ZHI，LIU JIANYE，YU FENG，et al.Research of airborne INS/CNS integrated filtering Algorithm based on celestial angle observation[J].Journal of Astronautics，2010，31（2）：397-403.（in Chinese）