优化目标可变的容错三维拓扑控制算法＊

王 东，邓 好

（湖南大学信息科学与工程学院，湖南长沙410082）

1 引言

Ad Hoc网络是指由一组自治无线设备组成的支持多跳的临时性的网络系统。网络中的所有节点在共享的无线信道上互相通信，无需任何网络基础设施，且具有易于快速部署的特点，使其在应急通信、交通管理、现代化生产、医疗卫生、环境监测等领域中得到广泛应用。因此，Ad Hoc网络通信技术受到了研究人员的广泛关注。

无线网络的拓扑结构是基于节点的物理位置和信号传输范围自治形成的［1］。在Ad Hoc网络中，一方面，节点的物理位置由任务需求来确定，另一方面，节点的信号传输半径可以根据需求进行调节。如果所有节点都以最大传输功率工作，节点有限的能量将被通信部件快速消耗，造成节点过早死亡，使得网络局部断开，甚至网络不连通；另外，节点以最大功率传输会使得节点信号彼此过度重叠，造成无线信号互相干扰，影响节点的通信质量，降低网络的吞吐率。为了有效解决以上问题，在Ad Hoc网络中有必要针对任务需求，对节点的传输功率进行调节，从而对无线网络的拓扑进行控制。

由于Ad Hoc网络中节点能量受限，节点工作一段时间后将会死亡，另外，任务需求也可能使节点发生移动，所以Ad Hoc网络中节点加入和离开网络等异动情况是经常发生的。节点的频繁异动使得网络拓扑结构动态变化，从而对网络的性能（如节点能耗、网络传输能力等）产生很大的影响。此外，在实际应用中，网络的通信场景会发生变化，当多个节点同时通信或部分节点发送大量数据时，其信号不间断，会对其他节点造成干扰，造成网络通信质量下降，此时降低干扰尤其重要；当节点不同时通信或节点发送数据少时，信号冲突几率低，干扰对网络影响不大，此时，拓扑控制优化目标应该以节约能量、延长网络生命周期为主。因此，如何研究出一种具有较好拓扑容错能力，能适应实际通信场景变化，同时能兼顾其它网络性能要求的拓扑控制算法成为Ad Hoc网络技术研究的热点。

本文提出一种适用于三维立体空间、可以根据网络干扰情况调整优化目标并且具有较好容错能力的拓扑控制算法——OVFSS（Optimization－Variable Fault－tolerant Spanning Subgraph）。

2 相关工作

早期的拓扑控制是通过调整节点发射功率在保持连通性的同时达到节能的目的，从而延长网络生命周期。Chew L P［2］第一次提出了伸展因子的概念，该因子等于通过拓扑控制技术调整后的生成子图路径能耗与原图路径能耗之比，来描述拓扑控制之后网络的能量伸展性。近期，一些研究工作也把注意力放到如何调节功率，使网络保证连通的情况下同时满足能量伸展性。

Wang Y等人［3］最先开始研究如何通过减小节点的发送功率来降低网络总能耗，并且使调整后的通信子图具有能量伸展性。同时，他们还提出了两种启发式算法，使构建的网络能耗较低，且满足能量伸展性等要求。

Shpungin H等人［4］从理论上研究了伸展性问题，他们的目标是同时满足能量伸展性和距离伸展性。为了能量伸展性，他们提出了一种方法，使调整后的子网的能量伸展因子为2（即新导出的子图点对之间的路径能耗最多是原图的2倍），并且得到的子网是强连通的。

Rickenbach P V［5］提出降低网络干扰才是无线网络拓扑控制最重要的目标。无线网络中的干扰会导致网络拥塞和数据包的重传，对网络的生命周期和网络的可用性都有很大的影响。

上述工作主要考虑无线网络的能量有效性和如何延长网络的生命周期问题，而网络的容错能力也十分重要。无线网络的容错拓扑控制主要研究如何构建k连通的拓扑结构图，即在k－1个节点失效的情况下，网络仍然保持连通，相关的研究有文献［6～8］。但是，这些研究又缺少对其他性能的考虑，例如能量有效性等。

在无线网络领域，研究的重点集中在节能、减小干扰、容错等方面。为了简化算法研究，方便建模，一般假设网络部署在二维平面上。然而，实际应用时网络节点一般是分布在三维立体空间里。二维平面图和三维立体图在性质上有很大的差别，简单地将三维网络映射到二维会丢失许多几何性质，所以二维场景下设计的部分算法无法直接应用到三维。为了设计出更加真实、合理有效且可应用到实际网络中的拓扑控制算法，Wang Y等人［9］在三维场景下对无线网络的拓扑控制进行研究，他们提出了3D k－RNG、3D k－GG和3D k－YG三种算法，并且证明这些算法都具有一定容错能力，同时还分别满足部分网络性能指标。

由于三维场景的特殊性，针对三维场景所研究的拓扑控制算法还不多，面对Ad Hoc网络可能部署的复杂环境，追求单一优化目标或是固定优化目标的算法的实用性值得怀疑。为了算法的灵活多变性，本文提出一种优化目标可改变的容错拓扑控制算法。

3 数学模型

无线网络结构一般将其抽象成图，拓扑控制技术通过调节节点发射功率使得节点信号覆盖范围变化，影响节点之间的连通，可以抽象为图中边的增删。需要满足的网络性能要求，例如连通度、容错能力、干扰较小等，都可以抽象为对图的性质要求，对应为图的连通度、k连通、点干扰、边干扰等。

本文研究针对的是较为真实的三维应用场景，假设三维的Ad Hoc网络分布在一个三维空间R3上。网络用无向图G＝（V，E）表示，其中，V表示网络中所有节点组成的集合，E表示网络中所有边组成的集合。用｜V｜表示网络中的节点数，｜E｜表示网络中的边数。每个节点的发射功率都可以设置为从0到最大值Tmax之间的任意值。每个节点均有一个id号（IP或者MAC地址）。三维Ad Hoc网络的模型是个单位球UBG（Unit Ball Graph）。当且仅当u和v之间的欧氏距离dist（u，v）均不大于最大发射信号距离r时，u和v之间存在一条边。

无线信号在传播过程中信号会衰减，无线信号传播模型决定了节点发射功率和接收功率的关系。信号功率的衰减与发射天线和接收天线之间的距离的β次方成正比［10］，β是一个常数，取值范围由环境所决定，一般为2～5。β的取值与无线传播模型相关，对于自由空间模型，认为无线电波的损耗只和传播距离和电波频率有关系，在给定信号频率的时候，只和距离有关系。本文研究时采用该模型，取值β＝2，即给定信号频率时，电波损耗与传播距离的平方成正比。

对于节点集合V中的两个节点u和v，给出节点传输能耗、k连通、点干扰、边干扰的定义。

定义1 点u是图G中的一点，拓扑控制后，u的传输能耗为该节点能达到的最远距离邻居节点所需的能耗。

定义2 当且仅当图G＝（V，E）中的任意两点u和v之间存在顶点不相交的k条路径时，图G＝（V，E）是k连通的。也可以理解为，当去掉图G＝（V，E）中k－1个顶点，图仍然连通时，图G＝（V，E）是k连通的。

节点之间通信造成的干扰是一种概率性事件，为了能量化网络中的干扰，借鉴文献［11］定义干扰模型。节点u和v通信时，若存在节点w，且该节点w的发射区域覆盖了u或者v，则w的信号会影响u的发送或者v的接收，此时就可以理解为w对u或v造成了干扰。借鉴二维网络中经典的干扰模型，本文构建一种三维网络内节点通信干扰模型，定义如下：

定义3 节点u的干扰值I（u）定义为所有通信范围覆盖了节点u的节点数。I（u）＝｛v｜v∈V＼｛u｝，u∈Z（v，rv）｝，这里V表示网络图节点集合，Z（v，rv）代表以节点v为中心、rv为半径的球形通信区域。

定义4 边e＝（u，v）的干扰值可以定义为所有通信范围覆盖了边e中节点u或v的节点数。I（e）＝｛w｜u∈Z（w，rw）∪v∈Z（w，rw），e＝（u，v），w∈V｝。

图1为三维网络边干扰模型示意图，每个节点均以其发射功率能达到的通信距离为半径形成一个球状通信区域，假设节点u和节点v之间存在一条边，若节点u或v处于节点w的通信区域内，认为节点w对节点u、v之间的通信边造成干扰，该边的边干扰值加1，以此方法检查所有邻居节点，最终得出该边的边干扰值。

Figure 1 Edge interference model in three－dimensional network图1 三维网络边干扰模型

4 优化目标可变容错拓扑控制算法

实际应用的Ad Hoc网络拓扑控制算法需要综合考虑多个优化因素。以往的算法考虑多个优化目标时，由于各个优化目标（例如网络干扰和能耗）可能是互相矛盾的，一般在各项网络性能指标中取一个折衷值，部分优化干扰和部分优化能耗，是一种非最优化的静态平衡。实际情况下，网络通信状态是变化的，某时刻可能大量节点同时通信或部分节点发送大量数据，其信号对其他节点造成干扰，也可能某时刻节点处于监听状态，偶尔发送数据，彼此信号冲突较小，干扰较小。静态优化并不能适应这种变化情况，无法将优化目标最大化。针对应用场景通信环境信号干扰强烈程度多变的情况，提出一种优化目标可变的容错拓扑控制算法OVFSS，在保证网络k连通的前提下，根据节点通信情况判断网络所处情况，选择合适的参数，进行有针对性的目标优化。算法的具体思想是，根据网络通信情况，适当选择重点优化的目标。在干扰影响较大时优先减小干扰，保证网络应用能有效实施；在干扰影响较小时，不考虑干扰，优先降低能耗，以便延长网络生命周期。

文献［11］通过对干扰进行建模，将概率性事件进行量化。同样的路由算法下，当节点同时通信或部分节点发送大量数据时，数据冲突加剧，丢包、重传次数会上升，此时干扰对网络影响较大；当节点不同时通信或节点发送数据小，彼此信号冲突概率低时，丢包、重传次数会较小，此时干扰对网络影响较小。本文假设节点设备硬件和协议能通过重传、丢包等数据的统计，判断网络的干扰影响程度，干扰影响大时设置参数s＝1，干扰影响小时设置参数为s＝0。

为了减小网络中的干扰，可将边权值改为边干扰值，但同时也发现一个问题，如图2所示I（A，B）＝I（A，C）＝3，但此时邻居节点距离不相同，图2中可见，dist（A，B）＞dist（A，C），即单一考虑将边权值改为边干扰值考虑不周全。

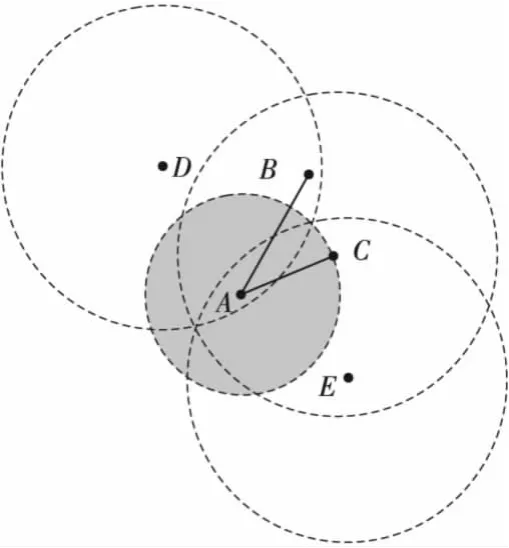
Figure 2 The case of same edge interference but different distances图2 边干扰相同距离不同情况

为此，OVFSS算法将综合考虑干扰和距离能耗等因素，定义边权值如下：

权值公式由两部分组成，第一部分是干扰影响值，第二部分是规格化后的距离影响值。s＝1时，权值公式主要由边干扰I（u，v）决定，同时规格化距离值能保证在节点干扰度相同的情况下，距离小的边权值较小；s＝0时，即干扰较小时，边干扰不纳入考虑，由规格化距离值决定权值，最大化地实现节能优化的目标。

要注意的是，寻找最小能耗生成子图已被证明是NP难问题，本算法考虑容错和多个优化目标时该问题显然也是NP难问题。

OVFSS算法根据边权值公式对图中所有的边的权重进行计算，然后按照边权值升序排列。根据得到的边权值，基于贪婪算法计算一个干扰最小的或能耗最小的k连通图。为保证贪婪算法是唯一结果，假设不相同的节点对之间的边权值没有相同的。算法的伪代码如下：

算法1 OVFSS

输入：具有N个节点的点集和连通度k（k≥1）。

输出：k连通的干扰最小或能耗最小的子图。

1：初始化原图G＝（V，E）。

2：计算G中每条边的边权值W＝s×I＋dist/r。

3：将所有的边按照边权值升序排列。

4：初始化子图GOVFSS＝（V，EOVFSS＝∅）。

5：对于图中的每条边e＝（u，v）。

6： 如果GOVFSS中u和v之间不是k连通

7： 添加该边到边集合中EOVFSS＝EOVFSS∪｛e｝；

9： 如果所有节点之间均是k连通

10： 退出，算法结束

当s＝0时，权值由距离决定，算法等价于Kruskal算法［12］的一种扩展版。该算法在保证容错的前提下，选取距离最短边以寻求节能优化，其干扰优化能力不强（本身就是在干扰较小的情况下才选择该算法）。

当s＝1时，边干扰值起决定作用，算法以干扰优化能力为主，同时兼顾选取距离较短、能耗较低的边，算法的优势体现明显。

下面对算法的正确性给出证明，即证明算法保证网络k连通的情况下优化网络干扰，使其干扰最小化，并同时考虑了节能。为了方便证明，本文采用以下术语：

G代表初始的拓扑图，G′代表算法优化后最终的拓扑图。Path（u，w1，w2，…，wn，v）表示从节点u到节点v的路径，其中w1，w2，…，wn代表路径经过的节点。Suv（G）代表无向图G中节点u到节点v之间的所有不相交的路径数。

引理1 设u1和u2是k连通无向图G中两节点，如果u1和u2间存在边（u1，u2），并且在图G中移除边（u1，u2）后，u1和u2之间仍然是k连通，那么G－（u1，u2）仍然是k连通的。

证明 要证明G－（u1，u2）是k连通的，等价于证明G′＝G－（u1，u2）中移除k－1个节点后，图G′仍然是连通的。不失一般性，假设｛u1，u2｝∩｛v1，v2｝＝∅。如果能够证明在图G′中移除k－1个节点后，任意两个节点v1、v2仍然连通，那么就可以证明G′是k连通的。

(4) 交通衔接条件：站点周边地区的交通可达性以及车站接驳体系的成熟程度，是制约客流的主要因素。本文主要选取车站周边道路网密度、人行道面积率、出入口周边机动车及自行车停放场地面积、公交车站经停线路数等指标，经过同等权重的无量纲化处理得到交通衔接水平评价值。

（1）如果v1、v2两个节点在原图G中直接相连，因为原图G是k连通的，那么很显然在图G′中移除k－1个节点后，节点v1、v2仍然是连通的。

（2）如果v1、v2两个节点在原图G中并没有边相连。假设图G″为G′－（k－1）个节点后的图。S1表示在G′中移除k－1个节点后Sv1v2（G′）中断开的路径数。因为Sv1v2（G′）是图G′中v1、v2两节点的不相交的路径数，所以在图G′中移除k－1个最多断开k－1条v1、v2节点间的路径，因此S1≤k－1。

①如果Sv1v2（G′）≥k，那么Sv1v2（G″）≥Sv1v2（G′）－S1≥k－（k－1）≥1。所以，在图G″中，v1、v2两个节点是连通的。

②如果Sv1v2（G′）＜k，这种情况只可能是在原图G中删除边（u1，u2）的时候断开了节点v1和v2之间的一条路径。所以，可以得到Sv1v2（G′）＝k－1。现在再考虑在图G′中删除k－1个节点后的两种情况。

a如果S1＜k－1，那么Sv1v2（G″）≥Sv1v2（G′）－S1≥1，即节点v1、v2两个节点是连通的。

b如果S1＝k－1，因为节点间的路径都是不相交的，S1＝k－1这种情况唯一的出现场景为v1与u1直接相连，v2和u2直接相连。用S2表示在G′中移除k－1个节点后Su1u2（G′）中断开的路径数，由命题题意可知Su1u2（G′）≥k，并且很容易知道S2≤k－1，这也就证明了在G″中u1和u2是连通的，又因为v1、v2分别与u1、u2相连，所以v1，v2是连通的。

综上可得，G′是k连通的，因此G－（u1，u2）是k连通的。证毕。□

引理2 假设无向图H和H′满足条件V（H）＝V（H′）。如果H是k连通的，并且每条边（u，v）∈E（H）－E（H′）在图G－｛（u0，v0）∈E（H）：W（u0，v0）≥W（u，v）｝中都是k连通的，那么H′也是k连通的。

证明 用集合E＝E（H）－E（H′）＝｛（u1，v1），（u2，v2），…，（um，vm）｝表示在图H中出现且在图H′没有出现的边集，且W（u1，v1）＞W（u2，v2）＞…＞W（um，vm）。同时定义一系列原图H的子图Hi：H0＝H，Hi＝Hi－1－（ui，vi）。下面用归纳法来证明：

（1）H0＝H，所以H0是k连通的。

（2）如果Hi－1是k连通的，那么应用引理1可得Hi是k连通的。所以，可以得到Hm是k连通的。

因为E（Hm）⊆E（H′），所以H′也是k连通的。证毕。□

定理1 G′是k连通的。

证明 在OVFSS算法中，所有的边都是按非递减顺序排列的，而且没有加入图G′中的边唯一的条件就是这条边的两个节点间已经是k连通的。应用引理2可以得到图G′是k连通的。证毕。□

定理2 优化干扰时，G′是一个干扰最小的k连通图。

证明 s＝1时，权值公式主要由边干扰值确定，边权值可以近似为边干扰值，用Sk（G）代表图G的所有k连通子图。如果G是k连通的，根据定理1，可得G′也是k连通的。假设边（u，v）是OVFSS算法中最后加入图G′的一条边。那么可以知道I（u，v）＝Max（u0，v0∈E（G′）｛I（u0，v0）＜I（u，v）｝，即I（u，v）的干扰值比已经加入到图G′中的任何一条边的干扰值都大。设G2＝G′－（u，v），因此在图G2中节点u和节点v之间的不相交路径数是小于k的，否则OVFSS算法不会将边（u，v）加入到图G′中。用图C＝（V（C），E（C）），这里V（C）＝V（G），E（C）＝｛（u0，v0）∈E（G）：I（u0，v0）＜I（u，v）｝。如果可以证明C并不是k连通，那就可以说在图G的任何一个k连通子图中都存在一条边的干扰值大于I（u，v），这也证明了G′是干扰最小的k连通子图。

用反证法证明C不是k连通的。假设C是k连通的，因此Suv（C）≥k。那么E（C）∉E（G2）；否则，｜Suv（G2）｜≥｜Suv（C）｜≥k，与前段中G2的定义矛盾。因此，E0＝E（C）－E（G2）≠∅。因为所有的边都是按干扰值非递减顺序加入到图G′中的，所以有∀（u1，v1）∈E0都满足u1和v1在图C－｛（u0，v0）∈E（C）：I（u0，v0）≥I（u1，v1）｝中是k连通的。由引理2可得，当把E0中的所有边都删除后，节点u和节点v之间仍然是k连通的，也就是说｜Suv（G2）｜≥k，而这与G2的定义是矛盾的。所以，由OVFSS算法得到的G′是原图G的干扰最小k连通子图。证毕。□

定理2证明了图G′是干扰最小的k连通图，在权值公式里，在干扰相同的情况下，选取边长更短的边，兼顾节能，以延长网络生命周期。在干扰较小时，权值公式改为由能耗决定边权值，此时通过类似定理2的证明过程可以得出，优化能耗时G′是一个能耗最小的k连通图。

5 仿真实验

考虑到3D k－GG算法和3D k－YG算法解决的问题与本文研究问题最为接近且是本领域具有代表性的算法，下面对OVFSS算法、3D k－GG算法和3D k－YG算法在干扰优化方面进行比较。

实验场景［8］为20×20×20的三维空间，节点的最大发射功率为9，节点数从50到175递增，β值取2。实验分别比较了干扰较强（s＝1）时不同容错度k＝1，k＝2和k＝3三种情况下，三种拓扑控制算法的干扰优化效果。当容错度k取1、2、3三个不同值时，仿真结果都是一致的：OVFSS算法降低网络干扰的能力都是优于其它两种拓扑控制算法。这里只给出k＝3时（容错能力度量值）三种拓扑控制算法的仿真结果。

Figure 3 Comparison of node interference among OVFSS，3D k－GG and 3D k－YG topology subgraph图3 OVFSS、3D k－GG和3D k－YG生成的拓扑图节点干扰比较

由图3可知，OVFSS算法生成的拓扑图的最大节点干扰和平均节点干扰值都是最小的，相对于原图UBG来说，OVFSS算法生成的拓扑图的点干扰值远远小于UBG图中的点干扰值，也同样小于其它三种拓扑图的点干扰值。3D k－GG算法生成的拓扑图的点干扰值要小于3D k－YG算法生成的拓扑图中的点干扰值。3D k－YG算法生成的拓扑图中的点干扰值相对于原图UBG来说还是有一定程度的减少。而且随着网络中节点数的增加，原图UBG和3D k－YG算法生成的拓扑图的点干扰值会线性增长，而OVFSS算法生成的拓扑图的点干扰值维持在一个较小的定值左右，并不会随着节点数的增加而增大。

由图4可知，随着节点数的增加，3D k－GG算法与OVFSS算法都可以有效地调节节点的发射功率，使得网络在保证k容错的同时，最小化网络中的干扰。OVFSS算法生成的拓扑图的边干扰值是最低的，远低于其它三种算法生成的拓扑图中的干扰值。而且随着节点数的增加，这一结果更加明显。

以上仿真结果表明，在三维空间网络中OVFSS拓扑控制算法的干扰优化效果都是较好的。

下面对OVFSS算法、3D k－GG算法和3D k－YG算法在能耗优化方面进行比较。

Figure 4 Comparison of edge interference among OVFSS，3D k－GG and 3D k－YG topology subgraph图4 OVFSS、3D k－GG和3D k－YG生成的拓扑图边干扰比较

实验场景［8］为20×20×20的三维空间，节点的最大发射功率为9，节点数从50到175递增，β值取2。实验分别比较了干扰较弱（s＝0）时不同容错度k＝1，k＝2和k＝3三种情况下，三种拓扑控制算法的能耗优化效果。当容错度k取1、2、3三个不同值时，仿真结果都是一致的：OVFSS算法降低节点能耗的能力都是优于其它两种拓扑控制算法。这里只给出k＝3时三种拓扑控制算法的仿真结果。

由图5可知，在同样大小的区域内，随着网络内部署的节点数的增加，网络节点密集程度上升，由于采用多跳短距离通信代替长距离通信，节点可以使用更小的传输功率来发送信息给邻居节点，再由邻居节点进行转发，3D k－GG、3D k－YG、OVFSS算法都能有效地调整节点传输功率，保证网络在k连通，并且在节点数目相同时，OVFSS算法在减小能耗方面要比其他两个拓扑控制算法效果好。

6 结束语

Figure 5 Comparison of node transmission power among OVFSS，3D k－GG and 3D k－YG topology subgraph图5 OVFSS、3D k－GG和3D k－YG生成的拓扑图节点传输功率比较

本文针对Ad Hoc网络可能应用在通信环境发生变化的场景，提出了一种更加真实的三维场景下优化目标可变的、保证k连通的容错拓扑控制算法，在干扰较强时，降低干扰并尽量节能；干扰较小时，重点考虑节能。并证明了该算法得到的通信子图干扰最小，并保证k连通。真实应用场景通信环境复杂，优化目标侧重点应该变化，需要综合考虑干扰优化，根据剩余能耗选择链路、网络容错性能、应用服务质量QoS（Quality of Service）保证等诸多问题，如何更加全面、合理地设置各部分影响因素对算法的影响需要进一步研究。

［1］ Wang Dong，Chen Wen－bin，Li Xiao－hong，et al.Distributed topology control algorithm for ad hoc networks using steered beam directional antennas［J］.Journal of Computer Research and Development，2010，47（3）：407－415.（in Chinese）

［2］ Chew L P.There is a planar graph almost as good as the complete graph［C］∥Proc of the 2nd Annual Symposium on Computational Geometry（SCG’86），1986：169－177.

［3］ Wang Y，Li X Y.Minimum power assignment in wireless ad hoc networks with spanner property［J］.Journal of Combinatorial Optimization，2006，11（1）：99－112.

［4］ Shpungin H，Segal M.Near optimal multi－criteria spanner constructions in wireless ad－hoc networks［C］∥Proc of IEEE INFOCOM’09，2009：163－171.

［5］ Rickenbach P V，Wattenhofer R，Zollinger A.Algorithmic models of interference in wireless ad hoc and sensor networks［J］.IEEE/ACM Transactions on Networking（TON），2009，17（1）：172－185.

［6］ Renato E N，Celso C R，Christophe D.Optimal solutions for fault－tolerant topology control in wireless ad hoc networks［J］.IEEE Transactions on Wireless Communications，2009，8（12）：5970－5981.

［7］ Li L，Lian L，Bin H.Algorithms for k－fault tolerant power assignments in wireless sensor networks［J］.Science China Information Sciences，2010，53（12）：2527－2537.

［8］ Indranil S，Lokesh K S，Subhas K G，et al.Distributed faulttolerant topology control in wireless multi－hop networks［J］.Wireless Networks，2010，16（6）：1511－1524.

［9］ Wang Y，Cao L，Teresa A，et al.Self－organizing fault－tolerant topology control in large－scale three－dimensional wireless networks［J］.ACM Transactions on Autonomous and Adaptive Systems（TAAS），2009，4（3）：1－21.

［10］ Rodoplu V，Meng T H.Minimum energy mobile wireless networks［J］.IEEE Journal on Selected Areas in Communications，1999，17（8）：1333－1344.

［11］ Cardieri P.Modeling interference in wireless ad hoc networks［J］.IEEE Communications Surveys ＆Tutorials，2010，12（4）：551－572.

［12］ Kruskal J B.On the shortest spanning subtree of a graph and the traveling salesman problem［C］//Proc of the American Mathematical Society，1956：48－50.

［13］ Wang D，Long W C，Li X H.Interference－aware fault－tolerant energy spanner in wireless ad hoc networks［J］.International Journal of Distributed Sensor Networks 2012，Article ID 235374，doi：10.1155/2012/235374.

附中文参考文献：

［1］ 王东，陈文斌，李晓鸿，等.自组网中基于自适应波束天线的拓扑控制算法［J］.计算机研究与发展，2010，47（3）：407－415.