一种基于类间类内双权重图像分块PCA的人脸识别技术

施志刚

（南通航运职业技术学院管理信息系，江苏南通226010）

0 引 言

近年来，主成分分析［1－5］（PCA）方法被广泛用于人脸图像的特征提取和识别．它基于K－L变换［6］提取人脸图像的主要成分．但是用此方法需要将二维图像矩阵转换成一维列向量，如果图像分辨率高，势必会引起特征提取计算的复杂度．并且PCA方法提取的是图像的全局信息，图像中的所有像素在特征提取中的作用相同，但是在人脸识别的过程中，这些图像往往会因光照、表情以及姿态等因素表现出很大的差异，因此传统PCA方法的识别效果并不理想．于是找出某种能减轻这些因素在提取有效鉴别特征中的影响的方法便成为提高识别性能的关键．

文献［7］基于传统的PCA方法提出了分块PCA算法．该方法不仅能有效地提取图像的局部信息，改善因光照和表情不同对特征提取所带来的干扰，还可以解决“小样本”问题．但此方法是根据所有训练样本分块图像的平均图像来建立总体散布矩阵，因此在特征提取时没有考虑到不同位置分块图像的特征差异．

为进一步提高人脸识别的正确率，本文提出一种新的方法．该法首先对训练样本图像建立同类图像空间，根据同类训练样本的平均图像与所有训练样本平均图像的距离，定义类间图像加权函数，以增强不同类图像在特征提取中的类间区分度，同时计算类内训练样本图像与该类平均图像的距离，定义类内图像加权函数，将此和类间加权函数相乘，这样每个图像均可获得一个权重．如果权重越小，说明此图像在特征提取中的作用越低；然后对训练样本图像分块，建立所有同位置加权子图像空间；最后基于新的样本空间对所有相同位置的子图像分别采用PCA方法提取特征，目的可以更好消除不同位置子图像之间的差异．

1 PCA方法

PCA算法基于K－L变换．在人脸识别中利用此原理可以提取人脸的主要成分，即特征脸空间，这样任何一幅图像都可以投影到此空间，并获得一组系数，用以人脸识别．

令ω1，ω2，…，ωc为C个模式类，A＝∈Rm×n，i＝1，2，…，C，j＝1，2，…，ni｝为训练样本集，其中：ni为第i类样本的个数，为训练样本的总数，表示第i个人第j幅图像．

总体散布矩阵可表示为

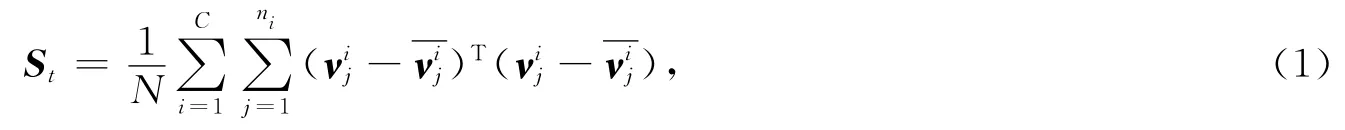
根据总体散布矩阵St，由式λU＝US求出一组正交的特征向量ut（t＝1，2，…，N）及其对应的特征值λt，将对应的特征向量ut按非零特征值λt从大到小的顺序排列．所组成的特征向量矩阵即为特征空间U，U的每一列为一个特征向量，即U＝．取前t（t＜N）个非零特征值所对应的特征向量作为正交矢量，组成新的特征脸子空间，有了这样一个降维子空间，任何一幅人脸图像矢量都可以在此获得一组投影系数，表示为

2 基于类间类内双权重图像的分块PCA方法

本文方法首先对训练样本图像建立同类样本空间，根据同类训练样本的平均图像与所有训练样本平均图像的距离以及类内训练样本图像与该类平均图像的距离，分别定义类间和类内图像加权函数，将它们相乘以获得每幅图像的权重；然后将图像分块，用权重乘以各自对应的子图像，构建同位置加权子图像空间；接着基于新的样本空间对所有相同位置的子图像分别采用PCA方法提取特征；最后用最近邻分类器分类，具体算法步骤如下：

2）定义类间加权函数．第i类训练样本图像的平均图像矩阵表示为，所有训练样本图像的平均图像矩阵表示为，第i类训练样本平均图像Ai与所有训练样本平均图像Γ的距离di用欧氏距离［8］可表示为，则第i类第j幅训练样本图像的加权函数可由式（3）定义：

3）定义类内加权函数．

第i类第j幅训练样本图像与该类平均图像的距离用欧氏距离可表示为，则第i类第j幅训练样本图像相对于该类的加权函数可由式（4）定义：

5）图像分块构造加权子图像样本空间．

将图像分块，用训练样本子图像矩阵乘以各自对应的权重形成同位置加权子图像样本空间，即为＝，每个训练样本图像矩阵分成p×q块，子图像矩阵是m1×n1矩阵，其中k∈［1，p］，l∈［1，q］，pm1＝m，qn1＝n．

6）基于新的样本空间分别求所有相同位置子图像矩阵的总体散布矩阵Gt．新的训练样本第kl分块子图像的平均图像向量表示为，其中．则所有kl分块子图像矩阵的总体散布矩阵Gt（kl）表示为

7）取总体散布矩阵Gt（kl）的前t个最大特征值所对应的鉴别矢量u1，u2，…，ut，得到最优投影矩阵Ukl＝［u1，u2，…，ut］．

9）设待测试样本图像矩阵Φx，对其第kl分块子图像向量（ψx）kl＝Vec（Φx）kl在特征空间Ukl＝［u1，u2，…，ut］进行投影，得到Φx第kl分块子图像的特征矩阵空间，即UT（ψx）kl＝［u1，u2，…，ut］T（ψx）kl＝（Yx）kl．

10）计算所有训练样本和待测试样本第kl分块子图像各自特征投影的距离，表示为

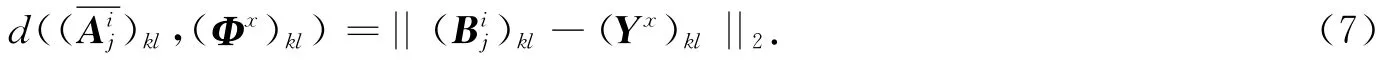
11）计算所有训练样本和待测试样本图像在特征脸空间各自投影的距离，可表示为

12）分类识别．

3 实验结果与分析

3．1 实验1

本实验在ORL标准人脸库上进行．该人脸库由40人、每人10幅、分辨率均为112×92的图像组成．这些图像拍摄于不同的时期，均有着不同程度的表情、姿态变化和细节差异等，如图1所示就是ORL人脸库中一个人的10幅图像．

本实验选取每人的前5幅图像作为训练样本，其余图像作为测试样本．图2为对原始图像矩阵进行4×2和4×4分块后分别采用本文方法得到的识别率与普通MPCA方法识别率的比较．两种分块方式下得到的子图像矩阵大小分别为28×46和28×23．

在人脸识别中，眼、鼻、嘴等部位为主要特征，按照这些特征对图像分块可使区分度增强，进而提高识别的正确率．为此本文采用4×2和4×4的分块方式．从图2的实验结果可以看出，在这两种分块方式下，本文方法较普通MPCA方法能在选取较少投影轴数的情况下达到较高的识别率，说明了本文方法的有效性．

进一步比较图2结果，可以看出本文方法和普通MPCA方法在4×2分块方式下的识别率均明显高于4×4分块．这是由于4×4分块较4×2分块在纵向上分块较多，这样会破坏人脸主要特征的完整性，从而对识别的效果产生干扰．因此，图像分块方式的不同是影响识别性能的因素之一．

图1 ORL人脸库中一个人的10幅图像Fig．1 Someone's 10images in ORL database

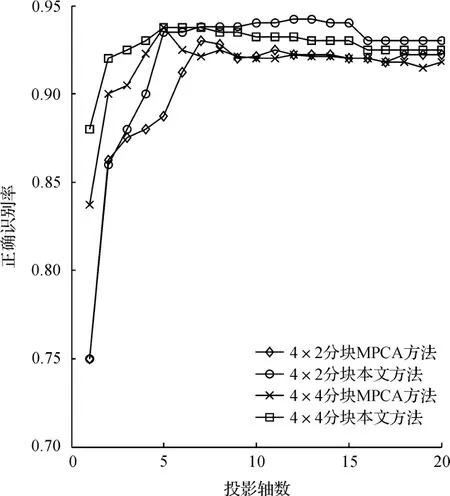
图2 ORL人脸库实验结果Fig．2 Experimental data in ORL database

图3 Yale人脸库中一个人的10幅图像Fig．3 Someone's 10images in Yale database

图4 Yale人脸库实验结果Fig．4 Experimental data in Yale database

3．2 实验2

本实验在Yale人脸库上进行．该人脸库由15人，每人11幅、分辨率均为100×80的图像组成．这些图像的光照和表情变化比较大．图3所示即为Yale人脸库中一个人的10幅图像．

本实验同样选取每人的前5幅图像作为训练样本，其余图像作为测试样本．图4为对原始图像矩阵进行4×2和4×4分块后分别采用本文方法得到的识别率与普通MPCA方法识别率的比较．两种分块方式下得到的子图像矩阵大小分别为25×40和25×20．

从图4可以看出，在4×2和4×4分块方式下，本文方法较普通MPCA方法为达到相同的高识别率，所需投影轴数明显要少，并且当投影轴数增加到一定数目，识别率达到最高时便开始趋于稳定．在4×2分块方式下，为达到最高识别率，普通MPCA方法所需的投影轴数为10，而本文方法选取4个投影轴即可达到此识别率；在4×4分块方式下，普通MPCA方法需9个投影轴才可达到最高识别率，但本文方法只要选取3个投影轴便可达到此识别率，这说明本文方法可以有效地改善识别性能．

此外，对比图2和图4结果发现，基于ORL人脸库无论是本文方法还是普通MPCA方法得出的实验数据都要明显好于Yale人脸库．进一步分析，这是由于ORL和Yale人脸库图像的组成有很大差异．在ORL人脸库中，每个人的脸部表情、姿态和细节等均有着不同程度的变化，其中人脸姿态变化的程度最大，深度旋转和平面旋转高达20°，人脸尺度的变化也多达10%；而在Yale人脸库中，每个人的姿态变化很小，主要是表情和光照的变化较大，因此两种方法都对有较大旋转和尺度变化图像的识别效果好．

4 结 语

普通MPCA算法能提取图像的局部信息，改善因光照和表情不同对特征提取所带来的干扰，同时图像分块可以避免使用矩阵的奇异值分解，有效降低了问题的复杂度；为进一步改善识别性能，本文结合分块图像的思想，根据同类训练样本的平均图像与所有训练样本平均图像的距离以及类内训练样本图像与该类平均图像的距离，分别定义类间和类内图像加权函数，构造加权子图像空间，用以特征提取．在ORL和Yale人脸库上的实验结果表明，此方法的识别性能优于普通MPCA算法，但是在实验中也发现，基于不同的人脸库，采取相同的分块方式，所获得的识别率也不同，甚至相差很大．这是由于ORL和Yale人脸库图像组成的差异，因此能否找出一种方法，使得适应性更强，在不同人脸库上均有着同等的高识别率是今后研究的方向．

［1］Kirby M，Sirovich L．Application of the KL procedure for the characterization of human face［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，1990，12（1）：103－108．

［2］Turk M，Pentland A．Eigenface for recognition［J］．Journal of Cognitive Neuroscience，1991，3（1）：71－86．

［3］Belhumeur P N，Hespanha J P，Kriegman D J．Eigenfaces vs．fisherfaces：recognition using class specific linear projection［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19（7）：711－720．

［4］张翠平，苏光大．人脸识别技术综述［J］．中国图象图形学报，2000，5（11）：885－894．

［5］胡静．基于代数特征的若干人脸识别方法研究［D］．南京：南京理工大学，2003．

［6］彭辉，张长水，荣钢，等．基于K－L变换的人脸自动识别方法［J］．清华大学学报：自然科学版，1997，37（3）：67－70．

［7］陈伏兵，杨静宇．分块PCA及其在人脸识别中的应用［J］．计算机工程与设计，2007，28（8）：1889－1892．

［8］孙即祥．现代模式识别［M］．2版．北京：高等教育出版社，2008：184－187．