两类一致等时系统的中心条件和极限环分支*

桑 波

(聊城大学数学科学学院，山东 聊城 252059)

考虑n次多项式微分系统

(1)

其中max(deg(Pn),deg(Qn))=n。当δ=0时，系统(1)以原点为中心或细焦点。如何区分称为中心焦点判定问题。

为了获得系统(1)具有中心的充要条件，首先需要计算系统的前面各阶非零焦点量并对它们进行零点分解，从而得到原点为中心的必要条件；然后利用首次积分、形式首次积分、积分因子或时间可逆性证明所得条件都是充分的。

近二十多年以来出现了很多焦点量算法，比如奇点量算法[1]、基于伪除的形式幂级数法[2]和摄动算法[3]。但当Pn,Qn为非齐次多项式时，系统(1)的焦点量非常复杂且难于约化，为此作者基于重新参数化法给出了焦点量的约化方法[4]。

从一个奇点分支出多个小振幅极限环的现象称为多重Hopf分支。设系统(1)以原点为M阶细焦点，则对其进行适当的系数微扰，相应系统至多可分支出M个小振幅极限环。至于实际扰动出多少个极限环，还需要作进一步的分析。

下面考虑n+1次多项式微分系统

(2)

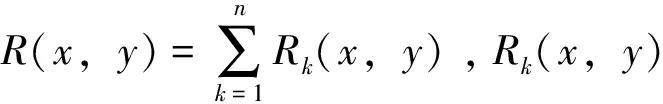
(3)

所以我们称系统(2)δ=0为一致等时系统。

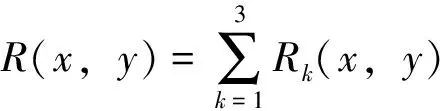
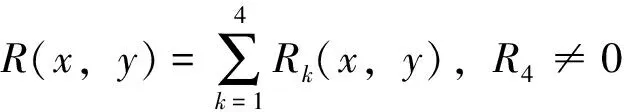
考虑如下两类系统

(4)

(5)

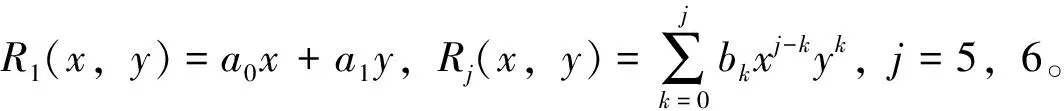
1 系统(4)的中心条件和多重Hopf分支

根据文[4]的计算方法，系统(4)δ=0的前5阶约化焦点量(不计非零常数因子)分别为

定理1 系统(4)δ=0以原点为中心的充要条件是下列5组条件之一成立

(ii)a1=b1=b3=b5=0;

(iii)a0=a1=0;

(iv)a0=b0=b2=b4=0;

其中

证明(必要性) 通过求解多项式集G={W3,W4,W5}，共得到定理中的5组独立系数条件，从而必要性得证。

(充分性)当条件(i)成立时，系统(4)δ=0的向量场关于直线a0x+a1y=0对称，因此由Poincaré对称原理，系统(4)δ=0以原点为中心。

当条件(ii)成立时，系统(4)δ=0的向量场关于y轴对称，因此它以原点为中心。

当条件(iii)成立时，由文献[5]知系统(4)δ=0以原点为中心。

当条件(iv)成立时，系统(4)δ=0的向量场关于x轴对称，因此它以原点为中心。

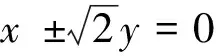
由系统(4)δ=0的焦点量结构和定理1知，系统(4)在原点邻近至多存在3个小振幅极限环。以下构造由5阶细焦点扰动出3个小振幅极限环的实例。

定理2 假设系统(4)满足

x4y+b2x3y2+

其中a0≠0，则当ε=0时，系统(4)以原点为5阶细焦点；当0<|ε|≪1时，在原点充分小邻域内系统(4)恰有3个小振幅极限环，其位置分别在圆x2+y2=k2ε2附近，k=1,2,3。

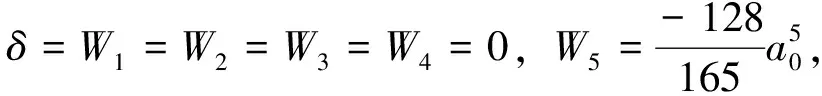
当0<|ε|≪1时，系统(4)的第0阶至第5阶焦点量依此为

v3(2π)=v5(2π)=0,

所以系统(4)在原点邻域的拟后继函数为

从而由文[10]知，系统(4)在原点的充分小邻域内恰有3个小振幅极限环，其位置分别在圆x2+y2=k2ε2附近，k=1,2,3。

2 系统(5)的中心条件和多重Hopf分支

通过计算，系统(5)δ=0的前6阶约化焦点量(不计非零常数因子)分别为

W1=W2=0,

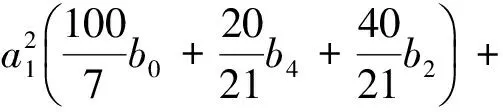
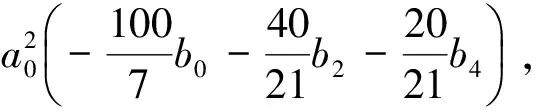
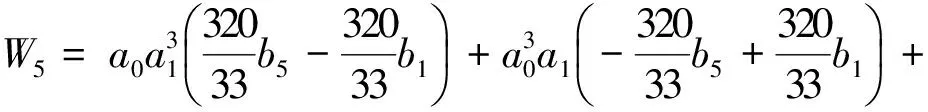
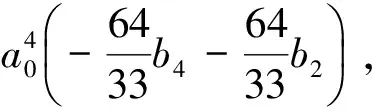
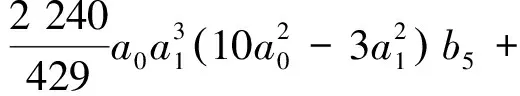
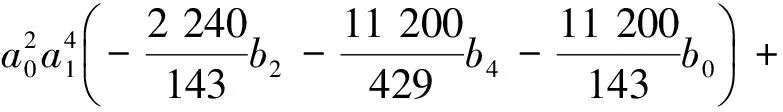
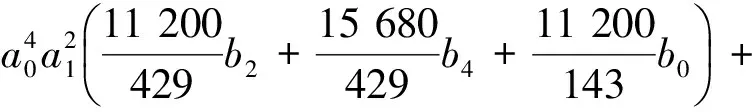
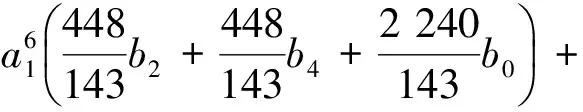
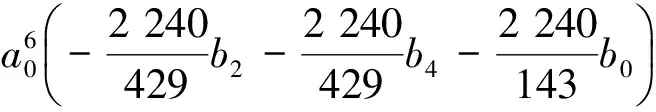
定理3 系统(5)δ=0以原点为中心的充要条件是下列7组条件之一成立：

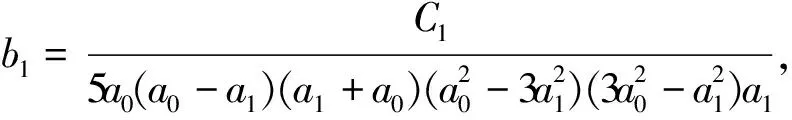
(ii)a0=±a1,b1=-b5,b2=-b4,

b3=0,b6=-b0;

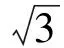
(vi)a0=b0=b2=b4=b6=0;

(vii)a1=b0=b2=b4=b6=0,

其中

证明(必要性)通过求解多项式集G={W3,W4,W5,W6}，共得到定理中的7组系数条件，从而必要性得证。

(充分性)当条件(i)成立时，系统(5)δ=0的向量场关于直线a0x+a1y=0对称，因此由Poincaré对称原理，系统(5)δ=0以原点为中心。

当条件(ii)成立时，系统(5)δ=0的向量场关于直线x±y=0对称，因此它以原点为中心。

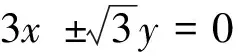
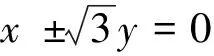
当条件(v)成立时，由文献[5]知系统(5)δ=0以原点为中心。

当条件(vi)成立时，系统(5)δ=0的向量场关于x轴对称，因此它以原点为中心。

当条件(vii)成立时，系统(5)δ=0的向量场关于y轴对称，因此它以原点为中心。证毕。

由系统(5)δ=0的焦点量结构和定理3知，系统(5)在原点邻近至多存在4个小振幅极限环。以下构造由6阶细焦点扰动出4个小振幅极限环的实例。

定理4 假设系统(5)满足

其中a0≠0， 当ε=0时，系统(5)以原点为6阶细焦点；当0<|ε|≪1时，在原点充分小邻域内系统(5)恰有4个小振幅极限环，其位置分别在圆x2+y2=k2ε2附近，k=1,2,3,4。

证明当ε=0时，由条件及焦点量公式，我们得到δ=W1=W2=W3=W4=W5=0,

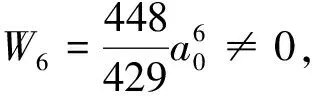
当0<|ε|≪1时，系统(5)的第0阶至第5阶焦点量依此为

v3(2π)=v5(2π)=0

所以系统(5)在原点邻域的拟后继函数为

从而由文[10]知，系统(5)在原点的充分小邻域内恰有4个小振幅极限环，其位置分别在圆x2+y2=k2ε2附近，k=1,2,3,4。

参考文献：

[1]刘一戎，李继彬．论复自治系统的奇点量[J]．中国科学A辑：数学，1989, 19(3)：245-255．

[2]WANG D M. Mechanical manipulation for a class of differential systems [J]. Journal of Symbolic Computation, 1991, 12(2): 233-254.

[3]YU P. Computation of normal forms via a perturbation technique [J]. Journal of Sound and Vibration, 1998, 211(1): 19-38.

[4]桑波，朱思铭．一类微分系统的非退化中心问题[J]．系统科学与数学，2013，33(5)：599-606．

[5]CONTI R. Centers of planar polynomial systems: A review [J]. Matematiche, 1998, 53(2): 207-240.

[6]CHAVARRIGA J, GARCíA I A, GINé J. On integrability of differential equations defined by the sum of homogeneous vector fields with degenerate infinity [J]. Int J Bifurcation and Chaos, 2001, 11(3):711-722.

[7]ALGABA A, REYES M, BRAVO A. Uniformly isochronous quintic planar vector fields [C]∥Fiedler B Proceedings of the International Conference on Differential Equations, Vol 2.World Scientific Publishing, Berlin, Germany, 1999, 1415-1417.

[8]GASULL A, PROHENS R, TORREGROSA J. Limit cycles for rigid cubic systems [J]. J Math Anal Appl, 2005, 303(2): 391-404.

[9]DIAS F S, MELLO L F. The center-focus problem and small amplititude limit cycles in rigid systems [J]. Discrete and Continuous Dynamical Systems-Series A, 2012, 32(5): 1627-1637.

[10]刘一戎，李继彬．平面向量场的若干经典问题[M]．北京：科学出版社，2010．