Lanchester竞争模型及其在公共交通投资中的应用*

朱 萌， 汪 泓

(1. 上海交通大学安泰经管学院，上海 200052；2. 上海工程技术大学基础教学学院，上海 201620)

上海“十二五公共交通发展战略和目标”的指导思想是“坚持‘公共交通优先’发展战略，进一步提高公共交通设施供应水平、服务能力和运行效率，营造适度宽松、有序的乘车和候车环境，进一步降低市民公共交通出行成本占可支配收入的比例，不断增强公共交通吸引力，进一步提高节能减排水平，为广大市民提供符合国际大都市水平的公共交通服务。”而政府将“加大公共交通财政保障力度，将公共交通投入纳入公共财政预算体系，在现有公共交通政府投入体系下，研究完善政府长期扶持机制和政府购买服务制度。合理界定企业的公益性服务项目，促进公共交通行业可持续发展。”故而提高公共交通出行在市民出行中的比例，增加对公共交通的支出已经是势在必行。

上海市的公共交通包括轨道交通、地面公交汽电车、出租车和轮渡等四种形式。本文将集中对轨道交通和地面公交汽电车进行研究。一方面是因为市场份额，根据上海市综合交通2008至2012年的年度报告，上海公共交通日均客运量中轨道交通和地面公交汽电车在公共交通中所占比重从2003年的73.1%到2011年的80.7%，两者占公共交通客运量已超过八成；另一方面是因为公共交通的社会属性，虽然公共交通有四种形式，但是轨道交通和地面公交汽电车与出租车系统相比较，更强调社会效益，两者更接近提供同质服务。

上海公共交通“十二五”规划中已明确要以公交优先，加大对公共交通的投入力度，并设定了未来轨道交通和地面公交汽电车的客运量分别占公共交通比例的预定目标。但是，对于轨道交通与地面公交汽电车两类企业的投入分配还未明确，即决策部门怎样在各种形式的公共交通之间分配资源。而这将对上海“十二五公共交通发展战略目标”的实现产生重要的影响，所以有必要分析政府对轨道交通与地面公交汽电车两类企业的投入分配方案，以实现公共交通发展的预定目标，同时评估既往资源分配的合理性也将有助于提升未来公共交通投入的绩效。

本文将采用Bass扩散过程和Lanchester竞争模型，讨论政府对轨道交通与地面公交汽电车两类企业的投入分配。早期，Bass扩散过程被用于描述新产品的推广，然后被引申来刻画具有动态市场规模企业的市场份额变化。在上海实现公共交通发展与优化的过程中，轨道交通与地面公交汽电车占出行比例都将显著提升，所以采用Bass扩散过程来刻画未来的公共交通出行比例变动是可行的。

Lanchester竞争模型是一个双寡头竞争模型。轨道交通与地面公交汽电车之间的选择是具有排他性的，即乘坐轨道交通时不可能同时乘坐地面公交汽电车，于是在统计出行次数时，用轨道交通出行次数与出行总数的比例，以及地面公交汽电车出行次数与出行总数的比例分别衡量两者的市场份额，这体现了轨道交通与地面公交汽电车对“市场份额”的竞争性。另一方面，虽然轨道交通和公共地面交通都属于公共交通，从服务的角度看，两者具有互补性，但它们对吸纳财政投入时是竞争的，也就是说，当政府对公共交通的预算确定后，两者间将是“零和博弈”。由于在公共交通中，轨道交通和地面公交汽电车所占比重超过八成，所以本文采用Lanchester模型来刻画轨道交通和地面公交汽电车在承接财政投入方面的竞争，取得了比较好的效果。

1 理论模型

1.1 扩散过程

Bass扩散过程通常用于描述动态市场规模的变动特征。Bass扩散过程由Bass[1]提出。

假设q(t)是t时刻一个产品的市场占有额，Q(t)是累积占有额，则Bass扩散过程可以用式(1)表示

q(t)≡dQ(t)/dt=

[a+b(Q(t)/S)][S-Q(t)];Q(0)=0

(1)

其中，a为创新参数，b为替代参数，S为潜在市场规模。

1.2 投入资产模型构建

Lanchester模型是一个微分博弈理论中的重要模型[2],在动态市场份额时，用于研究双寡头市场的竞争。

由Lanchester模型，可得

i,j=1,2;i≠j

(2)

其中，si(t)为企业i在t时刻的市场份额；mi(t)为对企业i在t时刻的投入；ρi(mi,mj)为对企业i的投资的效果函数，是企业i投入为mi(t)而竞争对手企业j的投入为mj(t)时的二元函数。

显然，si(t)+sj(t)=1。由式(1)-(2)，可知

qi(0)=qi0

(3)

其中，qi(t)为企业i在t时刻的市场占有额。

由于qi(t)+qj(t)=q(t),且si(t)=qi(t)/q(t)。可得

2 最优解和理论分析

设公交企业的收益函数

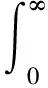
(4)

其中，gi为公交企业i的单位边际效益*为方便起见，这里暂不考虑投资成本。；μ为折现率。

由式(3)-(4)，可得Hamilton函数

Hi=giqi-mi+

(5)

由Hamilton方程的一阶条件可得

(6)

且

(7)

整理可得偏微分方程

λi(q-qi)·

(8)

一般情况下，偏微分方程未必有解析解。所以，只能根据投资的效果函数的性质去估计它的形式，这要求投资的效果函数ρi(mi,mj)满足如下性质。

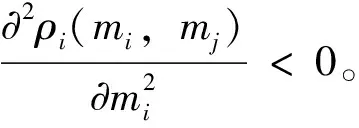
对于性质一而言，当竞争对手的投入固定时，随着己方投入的增加，效益当然也应该是越来越大的，所以要求效率函数是关于自己投入的增函数；对于性质二而言，当竞争对手的投入时，虽然随着自己投入越来越大，效率越来越大，但是效率增加的幅度是越来越小。

故而，本文构建投资的效果函数的形式如下

(9)

这里，c1,c2是两个独立常数。

显然，ρi(mi,mj)满足性质一、二。 由于mi>0和mj>0，以及因为政府在公共交通每年的投入会有预算限制，所以假设第t年政府公共交通的预算限制为L(t)，即mi(t)+mj(t)≤L(t)。

所以，式(8)可以转换为

(10)

又因为mi(t)+mj(t)≤L(t)，可得式(10)的解为

(11)

3 案例研究

在引入投资的效果函数后，本文将对上海市2003-2011年对轨道交通和地面交通的数据进行研究，分析市场份额变化与财政投入分配方案的合理性。

3.1 估计参数c1,c2

由方程(2)

则

si(t)-si(t-1)=

([1-si(t-1)]mi(t)-si(t-1)mj(t))c1+

(12)

由2003-2011年上海市公共交通年报数据，可由回归计算得c1=0.000 245,c2=-0.000 183。见表1。

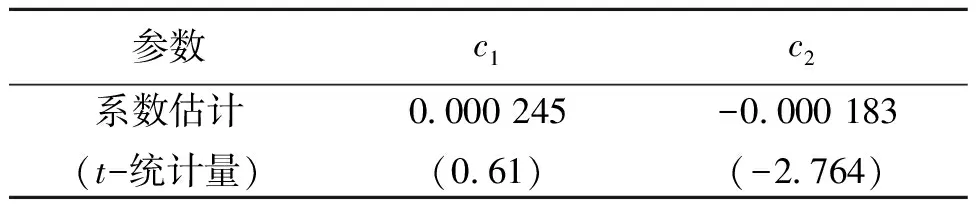
表1 Lanchester 模型参数的估计1)

1)模型的拟合优度R2=0.951

将c1,c2代入投资的效果函数，可得

3.2 估计Bass扩散过程的参数

由Erickson[3]的方法，可估计Bass扩散过程的参数。当i,j=1,2;i≠j，最优投入策略蕴含着下列方程

(13)

这里di是任意的常数。

明显的，对一般的正的折现率μ(μ>0)， 方程(13)没有解。而在零折现率下，方程(13) 有一个闭环解[1-4]。采用与Dung Nguyen等[5]相似的方法。在零折现率假设下，当i,j=1,2;i≠j，有

(14)

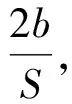
将k1,k2,k3代入式(2)，可得

表 2 Bass模型参数的估计1)

1)模型的拟合优度R2=0.993

将上面的参数代入方程(13)，可估计gi和di。

得到与Dung Nguyen等[5]相似的结论，d1和d2为零。见表3。

表3 其他参数的估计1)

1)模型的拟合优度R2=0.92

3.3 最优投资闭环解

在动态市场下比较轨道与地面公交汽电车的最优投资闭环解和实际支出情况，如图1所示。

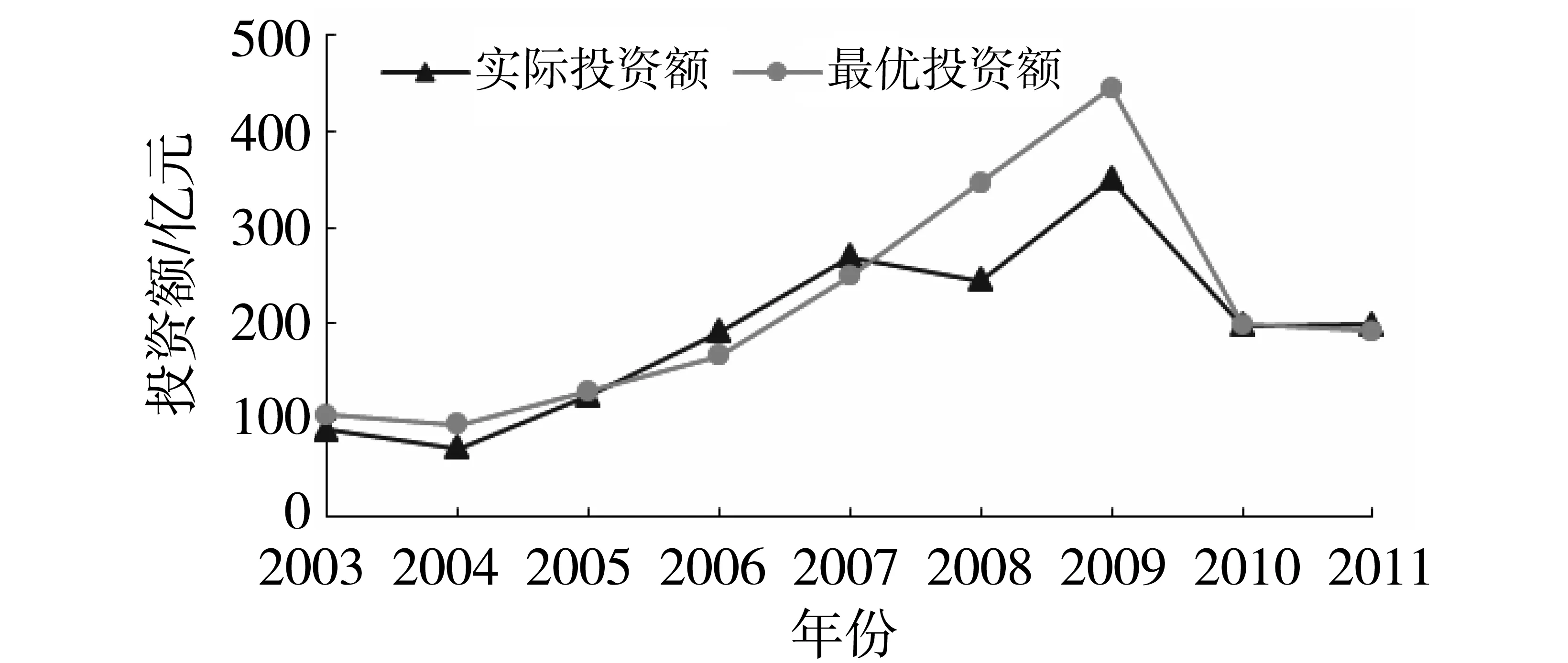
图1 动态市场条件下轨道交通实际投入与最优投入的对比

从图1中可以看到，在前期闭环解比较符合实际情况。就地面公交汽电车而言，也有类似的结果，如图2所示。

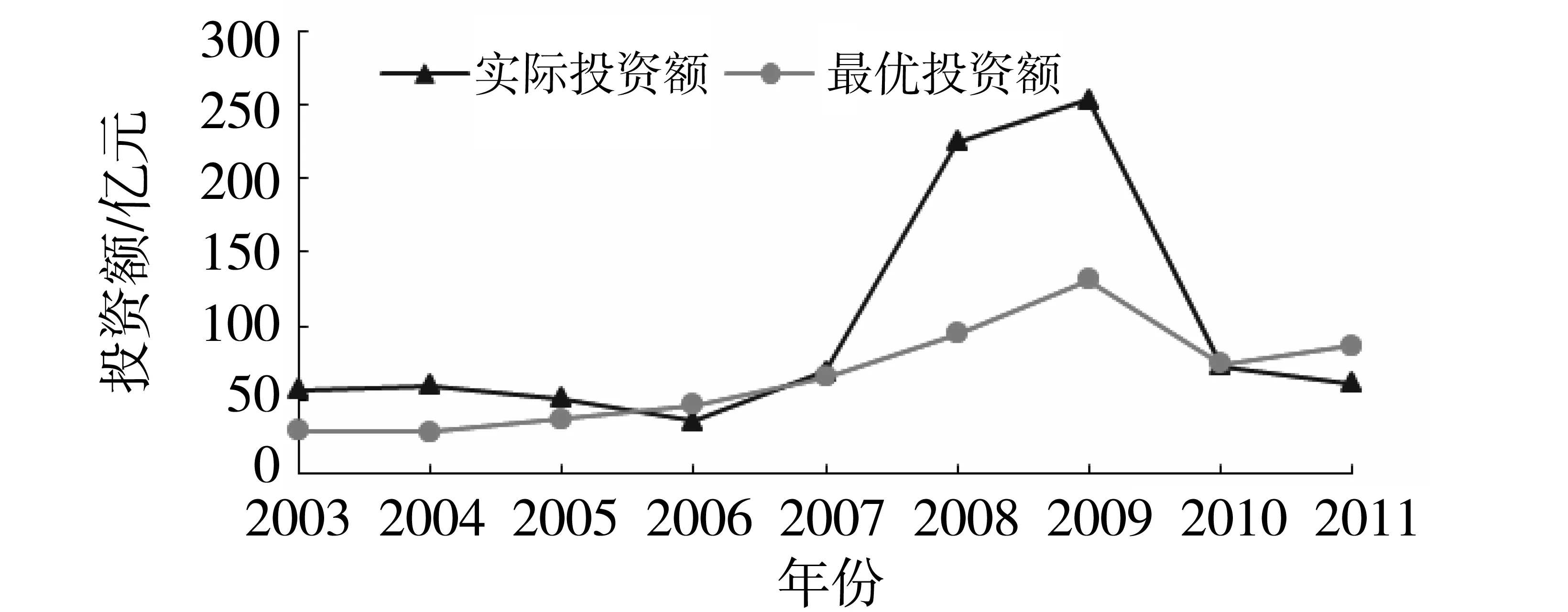
图2 动态市场条件下的地面公交汽电车实际投入与最优投入的对比

从图2中可以看到，大部分情况下，对地面公交汽电车的最优投资都在实际投资之下。

综合图1与图2，可知，在前期，轨道交通的投入是比较符合最优投入策略的，而在后期(2007年后)，轨道交通的投入明显不足。与此同时，在大部分时期内，地面公交汽电车的投入是比较符合最优投入策略的，但在2008年和2009年两年中，对地面公交汽电车的投入明显过度。实际上从上海市综合交通年度数据上就可以明显看到，从2003年以来，地面公交汽电车的出行次数一直都没有发生太大变化，日均客运量都在700万人次左右。

当然，这里有一个非常重要的原因。我们对地面公交汽电车投资的统计是源于2008至2012年《上海市综合交通年度报告》[6]，年报中对地面公交汽电车投资的项目有：城市道路、桥、隧道和公路。虽然我们在统计对地面公交汽电车投资时，只统计了对城市道路的投资，但实际上，这些对城市道路的投资不仅仅只是地面公交汽电车在使用，而是各种地面交通都在使用，从这个角度上去说，对地面公交汽电车最优投入应该比我们得到的最优投入要高。

总的来说，虽然对地面公交汽电车最优投入应该比得到的最优投入要高，但是结合图1的结论，我们认为优先发展轨道交通将更能体现公交优先。

3.4 最优投资分配比例

由上文分析可知，由于对城市道路的投资不仅仅只是地面公交汽电车在使用，还包括其他的各种地面交通，所以本文将从对轨道交通的最优投资的闭环解，测算最优投资分配比例，见表4。

表4 最优投资分配比例

轨道交通的投入分配比例的变化如图3所示

图3 轨道交通投入分配的最优比例与实际比例对比

图3说明在大部分年份中，财政资金对轨道交通的投入低于最优投资比例。因此，加大对轨道交通的投入是有必要的。

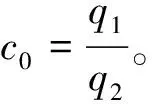
(15)

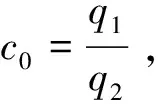
(16)

上海交通发展白皮书中，轨道交通的发展目标是“远期，轨道交通将成为公共交通的主体，客运量再翻两番，达到1 200万乘次/日，轨道交通和公共汽、电车的日客运量各占一半”。上海市城市公共交通“十二五”规划中明确指出上海公共交通发展目标是“公共交通出行比重(指使用公共交通方式的出行次数占所有使用交通工具的出行次数的比例)和客运量结构目标：中心城公共交通出行比重达50%，中心城轨道交通客运量占公共交通客运量的比重达50%左右。”另外，上海公共交通日均客运量中轨道交通和地面公交汽电车在公共交通中所占比重从2003年的73.1%到2011年的80.7%，如果预测远期，轨道交通和地面公交汽电车在公共交通中所占比重将达到85%，则c0=10/7,在长期m1(t)=1.87m2(t)，即对轨道交通的最优投资分配比例为65%。

4 结 论

本文在引入投资的效果函数后，讨论了动态市场规模和动态市场份额条件下公共交通的最优投入分配，主要结论包括：

1)依据公共交通发展的不同阶段投入效果来制定公共交通投资规划

由投资的效果函数可知，在闭环条件下，当竞争对手的投入费用固定时，随着己方投入的增加，己方的投资效率是越来越高，也就是己方投资效率与自身的投入正相关。由于公共交通业的特殊行业属性，无论是对轨道交通还是对地面汽电车增加投入，都对两者效益提升发挥推动作用，只是两者效率增加幅度不一样而已。这符合采用公共交通出行的实际情况，当出行距离较长时，人们通常选择搭配使用轨道交通和地面公交汽电车，因而对轨道交通或是对地面汽电车增加投入都将改善人们的出行状况。

目前，由于轨道交通的客运量占比小于地面公交汽电车的占比。根据上海市城市公共交通“十二五”规划目标，未来轨道交通的客运量的比例会占公共交通客运量一半，因此，现阶段应该提高轨道交通投入占比。

2)基于收益最大化的最优投资策略

当实际投入超过最优投入时，闭环下虽然会使己方的市场份额提高，但是总收益将降低。所以，虽然现阶段需要增加对轨道交通的投入，但不宜超过最优投资比例，否则公共交通(轨道交通的)总收益会降低。

3)政府决策者选择最优投入策略提供依据

本文测算的最优投入分配比例可为政府决策者提供最优投入策略选择依据，还可为财政投入绩效评估提供支持。

参考文献：

[1]BASS F M. A new product growth model for consumer durables [J]. Management Sci, 1969,15: 215-227.

[2]CASE J H. Economics and the competitive process [M]. New York: New York University Press, 1979.

[3]ERICKSON G M. Empirical analysis of closed-loop duopoly advertising strategies [J]. Management Sci, 1992, 38(12):1732-1749.

[4]CHINTAGUNTA P K, VILCASSIM N J. An empirical investigation of advertising strategies in a dynamic duopoly [J]. Management Sci, 1992, 38(9): 1230-1244.

[5]DUNG NGUYEN, LEI S. Competitive advertising strategies and market-size dynamics: a research note on theory and evidence [J]. Management Sci, 2006, 52(6): 965-973.

[6]上海市城市综合交通规划研究所.《上海市综合交通年度报告》[R].交通与运输,2008-2012年.