影像法测量螺纹时牙廓曲线的特征分析*

冯来健　陈曼龙　牛文莉

(1.陕西理工学院机械工程学院，汉中 723003)

0　引言

影像法测量螺纹是现代螺纹测量研究的热点，影像法测量螺纹主要是通过对待测螺纹进行投影，以牙形影像来反映待测螺纹，并按牙形影像轮廓的几何形状来获取待测螺纹参数的过程[1]。由于螺旋面是不断延伸的，螺纹不在同一平面内，在对其进行拍摄时，延伸的螺旋面对其它部分的螺旋面有一定量的遮挡，就造成了影像法测量螺纹时会出现牙廓“膨胀”和边界模糊不清的现象，直接利用这样的牙廓获取牙形参数必然存在测量误差[2-5]。所以，影像法测量螺纹时对牙廓曲线进行分段分析处理以及寻找各段曲线相交点是十分必要的[6-7]。

1　螺纹影像测量时牙廓分段情况分析

1.1　螺纹投影影像与分析

图1所示为以垂直投影方式按影像法测量具有阿基米德螺旋面的梯形右旋螺纹时的牙廓。为直接获取螺纹待测参数，按垂直投影方式进行影像法测量时是以牙顶、牙底为调焦基准[8]。可以看出牙两侧明显不清，这是因为以牙顶或牙底调焦的平面位于垂直投影方向的轴剖面内，而由于牙廓两侧螺旋面的延伸，使得投影轴剖面牙侧被其前、后延伸螺旋面牙廓遮挡，图1所示牙廓左侧被其轴剖面后的延伸螺旋面牙廓遮挡；而右侧则被其轴剖面前的延伸螺旋面牙廓遮挡，进而造成影像法获取的牙廓的牙形失真现象[9-10]。

图1　影像测量时的牙廓

由于以牙顶或牙根的清晰程度作为调焦依据，则牙顶(或牙根)不可能发生牙形失真，而且牙侧靠牙顶部分由于延伸螺旋面区域较小，进而遮挡少，牙形失真不十分显著；牙侧其余部分，特别是靠牙根部分由于延伸螺旋面区域较大，牙形失真会十分显著。如果把影像测量时获取的牙形轮廓进行简化，可以得到如图2所示ABCC′B′A′廓形。图中ADD′A′为理论牙形，AB(或A′B′)为较小遮挡曲线段，BC(或B′C′)为牙侧遮挡后的廓形。显然，牙形失真会让牙廓发生“膨胀”，而牙廓的“膨胀”则必然会造成牙形角增大、中径增大，给测量带来误差。

图2　牙廓失真情况示意图

1.2　影像分析

采用垂直投影测量螺纹必然会发生牙形失真问题，如果能计算出牙形失真量进行补偿，则可以明显提高测量精度[11-12]。为了分析失真情况，建立如图3所示的坐标系，螺旋面是以OP为母线具有阿基米德螺旋面的右旋梯形螺旋面，为了便于投影分析，用一个垂直于X轴的平面Ⅰ与螺旋面相截，所得交线Γ的形状如图3中所示。在进行图像获取时，理论上应该拍摄到的点E被实际拍摄到的点E′遮挡住了，就造成了失真现象的出现。

为了定量分析失真情况，假定图2中B点的坐标为(xB,yB,zB)，C点的坐标为(xC,yC,zC)，从牙形轮廓上看，在曲线弧AB段上，牙顶所在的螺旋线遮挡住了直径在(2xB,d)(d为大径)之间的螺旋线，交线Γ在(2xB,d)之间内任意位置时是单调递增的，也就是所拍摄到的弧AB是牙顶所在螺旋线的一段；在曲线弧BC段上，交线Γ的位置在(d1，2xB)(d1为小径)之间任意位置时，交线Γ上的最大值点是其他直径的螺旋线与Γ的交点，并不在大径所在螺旋线上，也就是所拍摄到的曲线弧BC是由最大值点组成的曲线。因为B点处在两段曲线的交点处，对所拍摄的牙廓形状有决定作用；C点是失真量达到最大时牙根部的点，对估量失真量有很大作用，所以，B，C是牙廓曲线上的两个关键点，弄清B，C点的位置很重要。

2　牙廓关键点的计算

(1)

图3　阿基米德螺旋面梯形螺纹

为求得该交线Γ上的Z坐标最大点，可对Z求Y的偏导

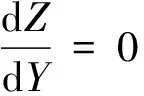
(2)

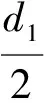
(3)

联立式(1)(3)，那么B点的坐标可以得到为

(4)

当以XOZ平面为测量平面即焦平面时，可求得曲线弧AB和弧BC的方程，曲线弧AB的方程为大径处的螺旋线在焦平面内的投影，即

(5)

0≤θx≤θB

曲线弧BC的方程为式(1)带入式(2)求得θ后在焦平面内的投影，即

(6)

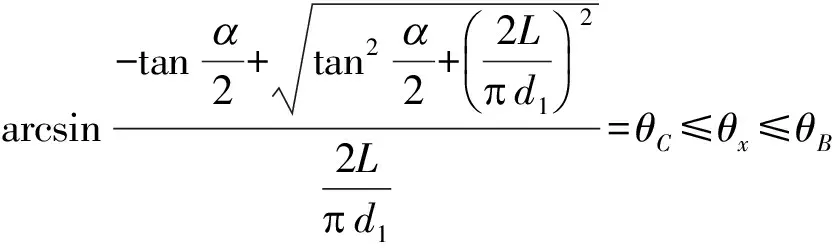
把式(6)中的θc值带入就可以得到C点的坐标为

(7)

3　牙廓曲线关键点的算例及实验验证

实验采用JVC300T二次元影像测量仪，对Tr24×5的右旋梯形丝杠牙形轮廓上取点并获得所取得点的坐标，然后进行曲线拟合得到交点计算式的过程。拟合曲线弧BC时，因为B点在牙顶附近，对牙廓取点时取牙顶和一侧牙廓点坐标即可，如图4(a)和表1所示。对点1～17进行最小二乘法二次拟合就得到了曲线弧BC的方程为

y=0.1429x2-1.1294x-10.1628

(8)

表1　JVC300T影像测量仪整个牙形所取点的坐标

拟合曲线弧AB时，鉴于曲线弧AB非常微小，对其放大12倍以后在同一个坐标系内取点并获得所取点的坐标，如图4(b)和表2所示。但是，因为曲线弧AB非常微小，采用最小二乘法二次拟合时，若有一个点有很小的取值偏差就可能导致拟合的结果有很大变化甚至是拟合曲线凸凹性的改变，而直接对所有10个点进行线性拟合，偏差同样也会很大，所以，对曲线弧AB采取线性拟合最后5个点的方法，这样就可以得到图2中曲线弧AB的拟合曲线方程为

y=1.7451x-18.0776

(9)

图4　JVC300T影像测量仪所取点位置示意

表2　JVC300T影像测量仪AB段局部放大取点坐标

在选取点坐标的时候应该注意，图4(a)中点20和21之间要有一段距离，点尽量不能取在这段距离之内，因为这段属于曲线弧AB，若有点取在其内部进行拟合曲线后会影响B点的坐标值，同样，图4(b)中点1和点10也尽量避免取到牙顶直线AA′和曲线弧BC内。

另外，通过分别对获取的牙顶和牙底轮廓上的多个点进行最小二乘法线性拟合，就可以得到图2中牙顶曲线的AA′和牙根曲线CC′的曲线方程，牙顶曲线的AA′的曲线方程为

y=0.0032x+11.5493

牙根曲线CC′的曲线方程为

y=0.0041x+8.0491

联合式(8)和(9)，求解方程组的解，可以得到交点B的坐标为(16.8232,11.3806)，C坐标为(15.8733,8.1142)，这两个坐标值是在测量仪自身建立的坐标系中的坐标值，和图3所示的坐标建立不同，为了便于图3坐标系中求得的理论结果与测量仪坐标系中求得的实际结果比较，把B点的位置和牙顶曲线AA′的位置进行对比，B点到牙顶曲线的距离是0.3225mm，所以就可以转换得到图3中B点的x坐标为11.9275mm,而通过理论计算式(4)，可以得到理论的计算结果是11.9051mm，通过试验和理论计算的结果进行对比可以发现，两者结果基本吻合，在误差允许范围之内，说明了理论计算式(4)的准确性。C点坐标用与B点的相对位置来验证，理论求得B、C之间x方向上的距离为0.7374mm，在y方向上的距离为2.6551mm，而实验求得的相对距离分别是0.9499mm和3.2664mm,误差分别为0.2575mm和0.6113mm，鉴于C点是拍摄时轮廓上距离焦平面最远的点，拍摄时最不清楚，所以，这个误差在可取的范围之内，说明了理论计算式(7)的准确性。

4　结束语

影像法进行外螺纹测量时会受到延伸螺旋面影响而发生“牙形膨胀”现象，在牙顶、牙中部及牙根部螺纹牙形受到影响的程度是各不相同的。螺纹牙侧靠牙顶部分受影响程度较小，而螺纹牙侧的中部，特别是靠牙根部份受到的影响程度是十分显著的，因此对影像法获取的螺纹牙廓进行分段分析和处理是十分必要的。本文通过对外螺纹影像测量时所获取牙廓分段情况的理论分析，用几何分析的方法给出了各段牙廓理论曲线方程及分段牙廓曲线交点的理论计算式，并通过对一种梯形螺纹实验验证，证实了对影像法获取的牙廓曲线进行分段处理的合理性，以及理论推演的各段廓线交点计算式的准确性。这对影像法螺纹参数的测量精度的提高或补偿具有重要意义。

[1]王世凯.用影像法测量螺旋面牙形时测量结果的双值性[J].陕西机械学院学报,1992,8(4):229-233

[2]王彩霞.线阵CCD非接触直径测量系统设计[J].自动化仪表,2012,33(4):41-44

[3]王珊珊.机器视觉大孔径大视场内调焦光学系统的研究[D].长春理工大学,2012

[4]何宝泉,雷振山.基于机器视觉的螺纹测量技术[J].计量技术,2005，(6):21-23

[5]蒋剑峰,张青春,姜招喜,柴国钟,鲁聪达.螺纹副虚拟旋合方法的研究及其应用[J].航空精密制造技术，2012,48(3):54-57

[6]Lili Ai，Feng Yuan，Zhenliang Ding.Measurement of spatial exterior attitude based on linear CCD[J].Chinese Optics Letters,2008,6(7):505-509

[7]Paul G.Ranky.Advanced machine vision systems and application examples [J].Sensor Review，2003,23(3):242-245

[8]颜发根,刘建群,陈新,丁少华.机器视觉及其在制造业中的应用[J].机械制造,2004，42(483):28-30

[9]陈曼龙.基于机器视觉的锥螺纹参数测量方法[J].计算机测量与控制,2012，20(5):1166-1167,1186

[10]陈曼龙.外螺纹垂直投影测量法及应用分析[J].激光技术,2012,36(6):793-797

[11]毕文波.基于机器视觉的机械零件尺寸识别研究[D].山东大学,2006

[12]卢丽燕.基于机器视觉的精密尺寸测量技术[D].中北大学,2008