基于PCA-ANN的水利工程标高金预测模型

石林林

(1.河海大学商学院,江苏 南京 211100; 2.河海大学项目管理研究所,江苏 南京 211100)

水利工程项目采购基本上采用招标投标方式,水利工程领域的竞争达到了空前激烈程度,施工企业面临着越来越大的竞争压力。水利工程建设投标报价的决策问题是一个非常复杂的过程,它不仅要考虑企业自身因素,还要全面考虑招标工程项目相关情况、招投标市场现状、竞争对手历史资料和投标可能性等因素。可见,投标报价关系到施工企业中标的可能性以及利润水平。要在激烈的市场竞争中生存下来以及得到进一步发展,企业必须要提高中标的概率。在水利工程投标竞争中,施工企业投标报价的合理性是获胜的关键,它主要取决于成本估算的准确性、其他影响因素以及这些因素和最终报价之间的关系。

水利工程投标报价主要由成本和标高金两部分组成,成本确定后,标高金主要由不可预见费和项目的利润构成。目前,投标报价模型主要有BP神经网络[1]、模糊自适应粒子群优化[2]、支持向量机[3]粗糙集与自适应模糊神经网络[4]、蒙特卡罗模拟方法[5-6]、不完全信息动态博弈分析[7-8]、仿真博弈[9]等。对比上述方法,BP神经网络的模拟程度更高,预测更接近真实值。这些文献选择了主成分BP神经网络的投标报价模型作为预测标高金的工具,先用主成分分析法(principal components analysis,缩写PCA)对影响标高金的多种因素进行数学降维,减少模型输入变量的数目,再利用BP神经网络(artificial neural network,缩写ANN)的自组织、自学习和非线性映射能力来找到大量数据中的内在联系和规律,客观而较为准确地预测出标高金。相比于其他模型,基于PCA-ANN的水利工程标高金预测结果更加具有信服力,操作上比较快速、简单、精确,有助于提高报价的准确性。

1 标高金影响因素的识别

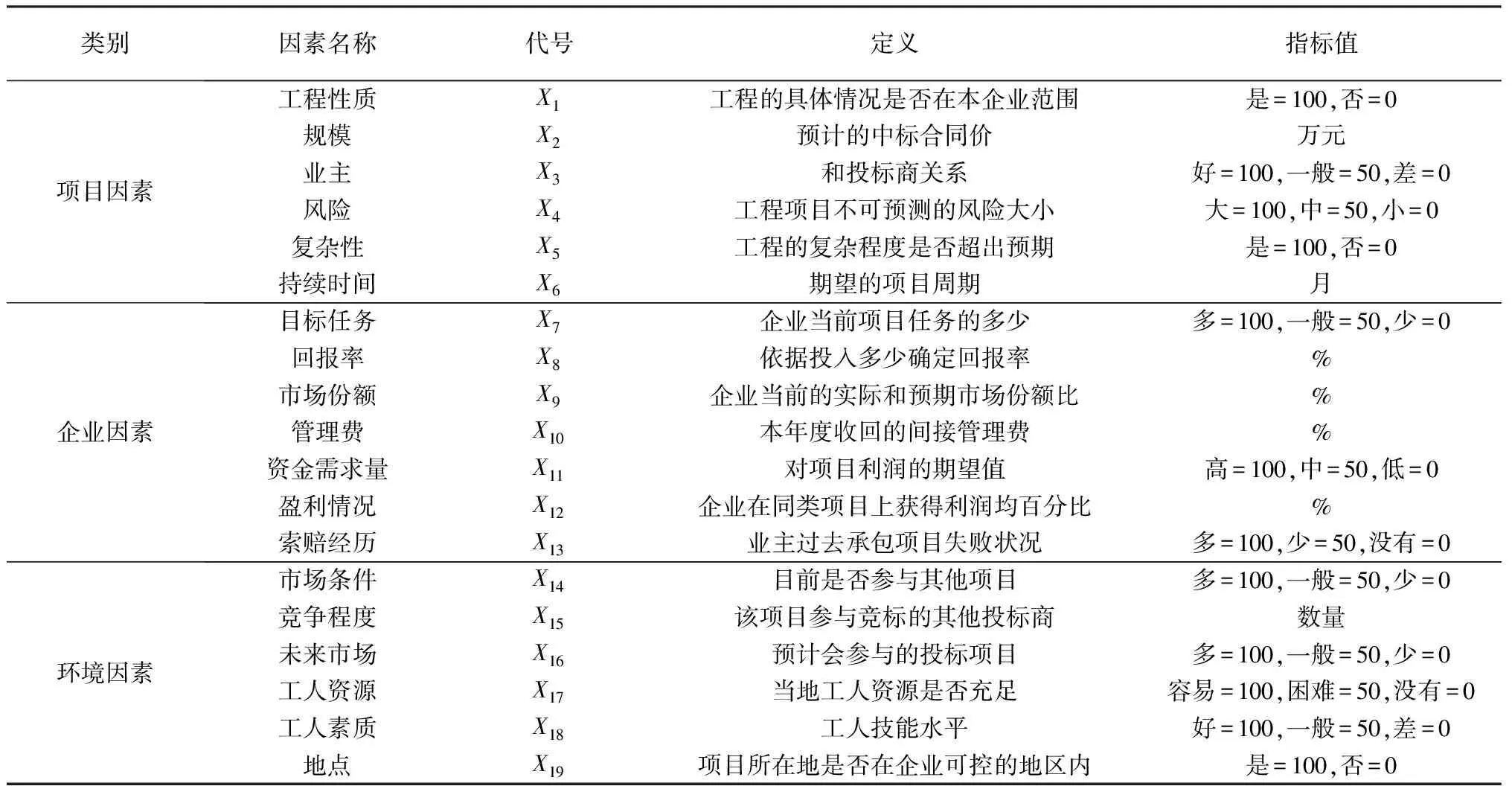
表1 投标报价影响因素的定义和指标值

2 基于PCA-ANN的标高金预测模型

2.1 主成分分析

选取标高金的影响因素应尽可能全面地覆盖投标报价的所有信息,使得预测模型结果更准确,但是过多的变量也会造成BP神经网络的过度训练,时间延长,反而结果可能不准确。为了提高模型的识别效率,应尽可能选择少的指标来代替原数据从而建立模型。通常可采用粗集理论或灰色关联分析的方法,但这两种方法实质上只是选择部分指标来代替原来信息,因此忽略了部分信息。而主成分分析方法应用了数学降维的方式,生成几个综合变量来代替原有的多个变量,同时又保证这些综合变量可以涵盖原有变量的信息,且相互之间互斥。即在不忽略或很少忽略原有信息量的前提下,把原有的多个相关的参数转换成少数几个互斥的综合参数。这样减少原有的指标数量,既解决了原有数据相关性的问题,又完成了对原始数据的降维工作。其基本算法如下[12]:

a. 取m维随机向量X=(x1,x2,…,xm)T的n个样品x=(xi1,xi2,…,xim)T,则X=(xij)n×m。

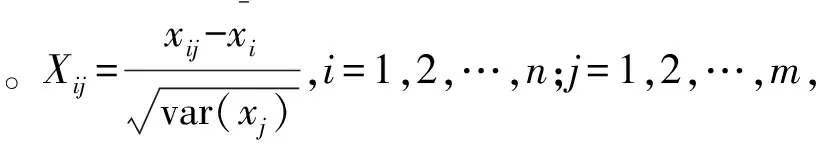
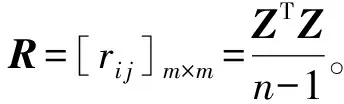
d. 计算样本的相关系数矩阵方程,得到m个特征值λ1～λm,其中λ1≥λ2≥…≥λm。

e. 解得主成分Y=UX。

当患者骨折、患有血管疾病等严重疾病时,往往需要长期卧床减少活动，导致血液循环速度变缓、身体免疫功能下降等生理状态改变，往往引起多种并发症，其中坠积性肺炎是常见并发症之一，容易导致病情加重甚至死亡[1]。有研究显示，脑卒中卧床患者坠积性肺炎发生率高达40%[2]。该疾病多起病隐匿，症状往往不典型，故临床注意预防，帮助患者保持呼吸道通畅，促进气道分泌物及时排出[3]。改良式体位引流是通过体位改变配合胸部手法如叩背、震颤等，促进痰液引流排出，具有较好效果[4]。2015年4月～2018年4月，我们对39例长期卧床患者实施改良式体位引流联合强化口腔护理，效果满意。现报告如下。

上述方法所确定的包含原指标信息量最多的成分称为第一主成分,其次是第二主成分。如果有K个指标,则可以得到K个主成分,但只有贡献率较大,一般是累计达到85%的前几个主成分就能覆盖绝大部分信息量,主成分标准化得分的大小和各个输入变量因子的绝对值大小、符号有关。测试值越大,则第一主成分标准化的得分就越大。

2.2 BP神经网络

神经网络是根据模拟人类大脑神经系统组织结构的原理来进行求解的。其中,目前神经网络技术的主流应用是BP神经网络,根据具体问题确定输入变量和目标输出变量,对BP神经网络进行设计,为神经网络选择适合的内部结构,主要包括选择网络的层数、每层的神经元数目和每层的激活函数等。

随着施工单位不断发展壮大,不断承接新的项目,企业过去投标的数据就会越来越完整,则建立ANN模型所需要的数据就会比较充分和完整,继而有利于标高金的预测。当网络的层数越多时,误差的平方和就会越小,神经网络预测的准确性就会提高。但过多的网络层数,又会使问题复杂化,增加训练的时间,使训练时间延长到几个小时甚至更长时间,不利于得出结果和优化结构。所以为提高速度,在设计中通常要尽可能地减少网络模型的层数,来减少网络的训练时间。一般来说,隐含层神经元个数的增多,会提高网络训练的精度。但在选择隐含层神经元数目的时候,要考虑到神经元数目的增加对训练时间的影响。训练时间由循环的次数和每一次循环所要耗费的时间所决定。如果神经元的数目过少,训练时间减少了,网络精度也会降低;如果神经元数目过多,既会增加训练的时间,网络训练又会有训练过度导致失常的可能。目前,快速选取隐含层神经元数目的做法是:在能够解决问题的前提下,适当地增加1～2个神经元即可。

2.3 PCA-ANN模型的构建

本文使用BP神经网络作为预测模型,网络输入端是标高金的影响因素,但由于影响因素较多,避免输入层的层数过多,导致训练过多目标层输出失常,反而结果会不准确,所以先用主成分分析法降维,减少输入端的网络层数,可以有效解决这一问题。输出端为标高金的预测值,模型的基本算法步骤如下:

a. 选取某一施工单位近几年的水利工程中标项目报价标高金原始资料。

b. 提取主成分。用PCA对输入变量进行降维处理,减少输入变量个数,确定神经元数目。选取累积方差85%的变量因子,降维处理后得到主成分变量因素。

c. 设计BP神经网络

①选择输入输出神经元数目。输入样本为影响投标报价的因素,其输出的特征向量为标高金,先确定输入层神经元的个数为降维后的个数和输出层的神经元数目。

②选择神经网络层次。根据Kolmogrov理论,对于任何在闭区间内的连续函数都可以用单隐含层的BP神经网络来逼近[13]。所以3层BP神经网络可以完成任意n维到m维的映射。也有研究结果表明,单隐含层的神经网络比多隐含层的神经网络的模拟结果有更高的精度。

③选择隐含层神经元数目。隐含层中神经元的个数要根据设计者的经验和反复的实验来确定。隐含层神经元的个数和实际的问题要求、输入和输出神经元数目都有紧密关系,如果隐含层神经元的数目过多,则会把样本中非规律性的内容也当成学习训练的内容,减低系统的泛化能力；如果神经元数目过少,网络从样本中获取信息的能力就会降低,不能够准确完全地反映样本规律。选用以往研究给出的经验公式来确定隐含层的神经元数目:

(1)

式中:n为输入层的神经元数目;m为输出层的神经元数目;a为1～10之间的常数。

根据以下公式确定的隐含层神经元的精度,精度最高的座位隐含层神经元数目。用总平均精度OAA来评价其优劣。定义OAA为

(2)

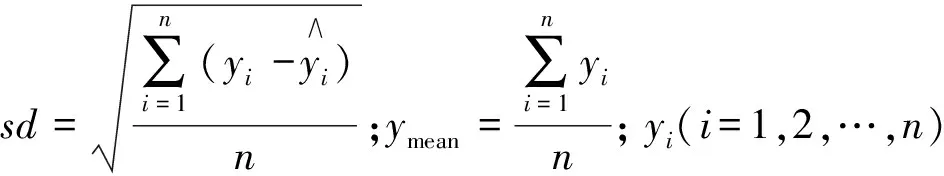
d. BP神经网络模型训练。可选用MATLAB软件帮助计算,先将原始数据进行归一化处理后,将主成分对应的数据作为输入变量,输出变量标高金。网络训练的终止条件设定为网络总误差小于0.1或者训练次数大于10 000，得到BP神经网络训练误差曲线。

e. 预测数据。选择几组组数据作为测试数据,输入网络中得到预测值,得到平均误差,分析是否满足要求。

3 案例分析

3.1 数据来源

数据来自于某一大型施工企业近五年的水利工程中标项目报价标高金原始资料,见表2。

X1～X19代表每次投标的影响指标的取值,Y代表了实际标高金(万元),N表示实例的个数。由于影响标高金的因素差异大,具有一定的代表性,所以经过训练得到的模型可以有广泛的实用性。选取表2的前27个实例进行ANN训练,训练结束后利用没有参与训练的后3个实例进行预测。标高金及其影响因素的指标值见表1。

3.2 提取主成分

由于变量1的指标值均为100,其方差等于0,可直接剔除不作为影响因素。再用SPSS数据编辑器将剩余18个影响因素指标值进行主成分分析,降维处理后得到9个主成分变量因素,见表3。

3.3 设计BP神经网络

先确定输入层神经元的个数为降维后的个数9个,输出层的神经元数目为1。根据公式(1),神经元数目为6～16,使用ANN模型进行训练,得到的网络模型总平均精度如图1所示。当隐含层的神经元个数选取11时,总平均精度达到最高点,为92.3%。

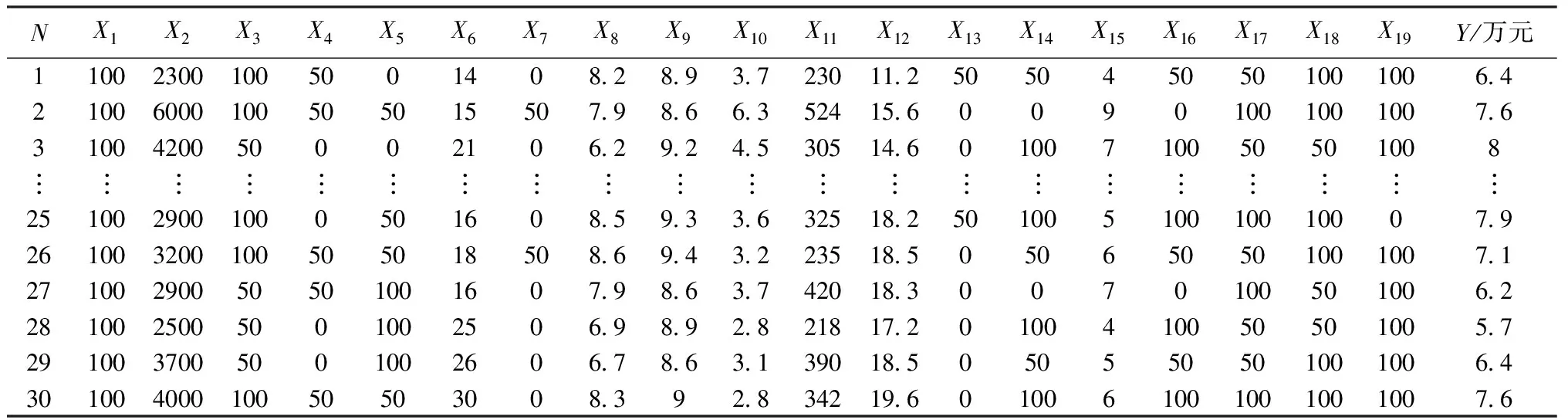
表2 标高金及其影响因素的指标值

表3 各主成分的方差贡献率及累积方差贡献率

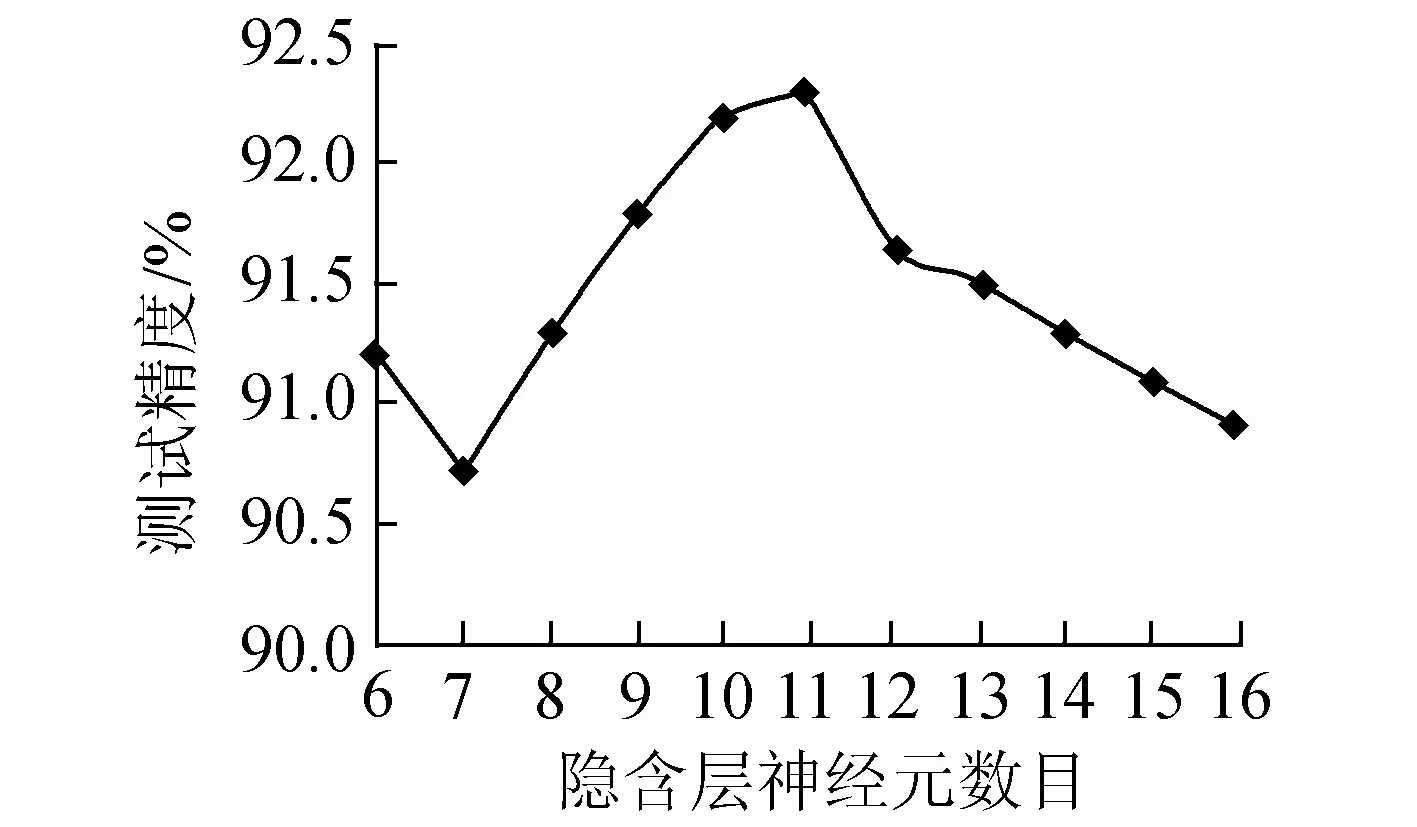
图1 不同数目的隐含层神经元产生的最好测试精度

所设计的BP神经网络投标报价预测模型选定为9-11-1的层次结构。

3.4 BP神经网络模型训练和预测

将1～27组的原始数据进行归一化处理后,9个主成分对应的数据作为输入变量,输出变量为1～27组的Y。BP神经网络训练误差曲线见图2。

图2 BP神经网络训练误差曲线

图2表明,BP神经网络在训练次数达到6 458次后总误差达到既定的要求0.1。用训练结束的神经网络开始进行预测时,将剩余的第28、29、30组数据作为测试数据,输入网络中得到预测值,结果见表4。

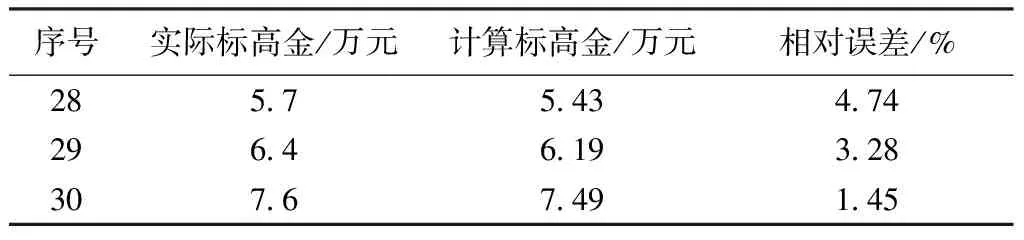
表4 BP神经网络预测结果

经计算,平均误差率为3.17%,用神经网络模型预测得到的标高金值接近于实际值,可以对投标报价进行合理预测。

4 结 论

a. PCA方法可重构多元变量输入状态空间,有效地避免了嵌入维数等参数的计算,能建立网络输入输出样本对。标高金的影响因素具有非线性、波动性、不确定性和复杂性的特征,PCA方法能使降维后的新向量较好地表征原始特征向量,有效地解决了原始特征参数维数过高的问题,使输入向量包含充分的预测信息。

b. 基于PCA-ANN相结合的标高金预测模型优化了BP神经网络建模方法的训练速度和迭代次数,可以准确地拟合原始样本。经过对模型的训练、检验,采用算例验证平均误差率为3.17%,说明此模型的预测精度较高,具有实际运用前景。

参考文献：

[1] 韩敏,林云,孙燕楠,等.基于神经网络的建筑行业投标报价研究[J].系统工程学报,2003(4):62-69.

[2] BAJPAI P,SINGH S N.Strategic bidding in network constrained electricity markets using FAPSO[J].International Journal of Energy Sector Management,2008,2(2): 274-296.

[3] 叶公伟,袁永博.基于最小二乘支持向量机的标高金预测方法研究[J].建筑管理现代化,2009(3):78-81.

[4] 喻刚,王雪青,赵辉.基于RS与ANFIS的投标报价决策研究[J].湖南大学学报：自然科学版,2008,35(5):94-97.

[5] 陈群,孙磊.蒙特卡罗法在投标报价中的应用[J].武汉理工大学学报：信息与管理工程版,2009(3):157-160.

[6] 宋维佳,张巍.基于先验信息的无标底投标报价策略研究[J].预测,2007(1):35-39.

[7] 陈起俊,梁宝栋.BQ计价模式下工程项目投标报价博弈模型研究[J].科技进步与对策,2012(18):68-71.

[8] PNGHO S,ASCE A M,LING Y,et al.An analytical model for analyzing[J].Journal of Construction Engineering and Management,2003,37(7): 102-109.

[9] NASSAR K.Pricing Construction Contracts in a Competitive Market: A Simulation Game[C]//ASC Proceedings of the 38th Annual Conference.Virginia Polytechnic Institute and State University-Blacksburg Virginia,2002: 47-54

[10] LIU S L,WANQ S Y,LAI K K.A general multivariate analysis approach for determining bid mark-up strategy[J].Construction Management and Economics,2005,23(4):347-353.

[11] FLORENCE Y Y,LIU M.Factors considered by successful and profitable contractors in mark-up size decision in Singapore[J].Building and Environment,2005,40(11):1557-1565.

[12] 张凌,李亚平.基于主成分和模糊聚类的区域自主创新环境评价[J].科技管理研究,2009(9):138-139.

[13] 罗松江,丘水生,陈旭.一种混沌伪随机序列复杂度分析方法[J].华南理工大学学报：自然科学版,2010(1):22-25.