基于比例二元语义的水利工程项目评价

冒小芬,陈建明

(河海大学商学院,江苏 南京 211100)

水利项目建设作为一项非常重要的基础设施建设,其社会性是其他项目无法比拟的。“十二五”期间我国水利项目的投资需求将超过万亿元,如此大规模资本的投入对项目决策的正确性提出了更高的要求,所以如何科学评价水利工程项目变得尤为重要。

目前进行水利工程项目评价的方法主要有模糊优选神经网络模型[1]、指标赋权法[2]和多层次模糊综合评价法[3]等。前2种方法的弊端在于水利工程项目有些指标可以定量计算,如经济评价指标，但是大量的评价指标不能或很难定量计算,只能采用定性描述,如社会和生态评价指标。多层次模糊综合评价法虽然实现了定性指标定量化,可是该方法最后的计算结果可能没有合适的预先定义的模糊数对应,只能用和结果最相近的模糊数表达,这近似的过程大幅度降低了评价结果的精确性。此外多层次模糊综合评价法计算的各指标评价的综合,并没有分开考虑各指标的评价结果,如果出现一种指标(如经济评价指标)足够高,而其他指标(如生态评价指标)明显低于某一标准,该方法的总评价指标是高的,但是这样的水利项目是不能上马的,因此评价结果有失科学性。

笔者根据上述评价方法存在的不足进行改进,在总结归纳了水利工程项目评价指标的基础上,提出基于比例二元语义的水利工程项目评价方法。二元语义是Herrera[4]首次提出的用二元组表示语言评价信息并进行计算,可以有效规避语言评价信息计算时出现的信息丢失和扭曲问题,使评价结果更精确。但二元语义存在以下缺点:①评价语言只能用预先定义的集合中选择,有时候专家认为指标的评价不是一定处于某个等级上,而是介于某2个等级之间,所以他不得不选一个和自己观点最接近的等级作为结果,这造成了初始数据的不准确;②二元语义所要求的评价语言术语必须是对称分布的,且距离是相等的,但大部分的术语集合并不符合这一要求。Wang等[5]提出的比例二元语义方法弥补了上述缺陷,专家可以用2个相邻等级的比例来表达自己的评价观点，而且所用的等级术语之间的距离也不是相等的,此外,判断矩阵模型将各个方面的指标评价情况清晰地表达出来,克服了第二个缺点。总的说来,比例二元语义方法保留上述方法的优点且改进了其中的不足,也是首次在项目评价应用的尝试。

1 水利工程项目评价指标体系的建立

水利工程项目的评价分为前评价、过程评价和后评价3种,这里主要涉及的是前评价部分。对于水利工程项目的评价,蒋水心等[6]提出指标体系涵盖5个部分:经济效果、社会效果、环境影响效果、科技管理效果和风险影响。丰伟等[7]总结提出了经济、技术、环境、社会影响四方面、14个指标的评价体系。张慧等[3]构建的评价体系包括除害兴利、政治社会、当地社会环境、技术方面和风险方面。

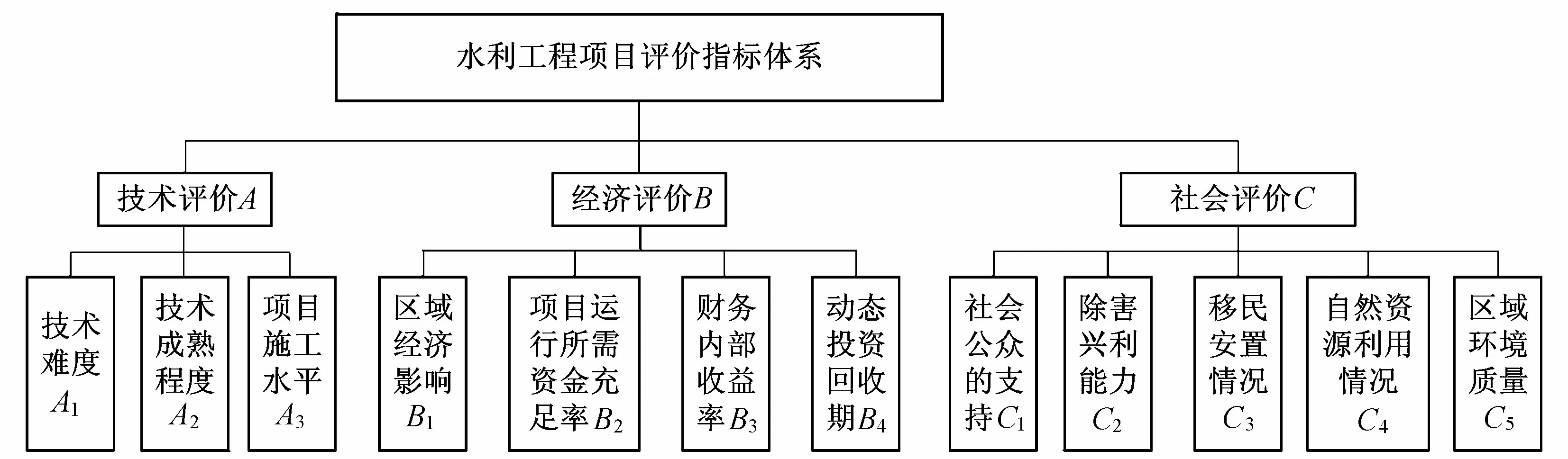
图1 水利工程项目评价指标体系

总结归纳以上研究成果可知,水利工程项目的评价体系由三部分构成:技术评价、经济评价和社会评价。技术评价是评价水利项目可实现性和实现的难度,具体指标有技术难度、技术成熟度和项目施工组织水平;经济评价是评价项目带来的经济效益,具体指标有区域经济影响、项目运行所需资金充足率、财务内部收益率和动态投资回收期;社会评价是指项目的社会公益性和可持续发展能力,具体的指标有社会公众的支持、除害兴利的能力、移民安置情况、自然资源利用情况和区域环境质量。为方便研究,指标用字母A，B，C表示,由此建立的体系如图1所示。

水利工程项目评价的结果由3个方面体现:技术评价、经济评价和社会评价。这3个方面都很重要,不能忽视任何一个方面,其中任一方面或者两方面不好都会影响其他方面的评价结果。比如,水利项目的技术不成熟,就会影响水利项目的建成,进而影响项目的区域经济影响和除害兴利能力;同理如果水利工程项目得不到社会公众的支持,项目的施工水平就会受到影响,区域经济影响也会相应大打折扣;其他类似的情况亦然。图2为水利工程项目的判断矩阵模型。

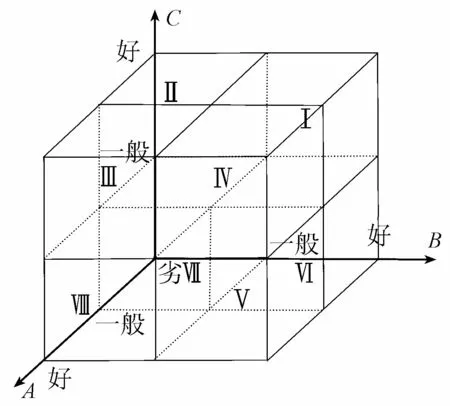
图2 水利工程项目的判断矩阵模型

2 基于比例二元语义的水利工程项目评价方法

2.1 比例二元语义评价理论

比例二元语义使得专家不必仅用一个评价语言而是可以用2个两虚的语言来表达自己的观点,比例二元语义评价是指用比例二元语义(αlt,(1-α)lt+1)表示针对某指标给出的评价结果,其中lt是预先定义的评价语言集合中的第t个,L={l0,l1,l2,…,ln}是有序评价语言集合,语序关系是若s>t,则ls>lt。

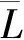
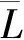
2.2 水利工程项目的评价方法

最初由Zadel[9-11]提出的语言评价为人类的推理、判断和决策提供了一种表达方式。在运用Delphi法评价水利工程项目时,大部分专家倾向于用语言而不是准确的数值来表达自己的评价观点,他们针对每一个指标的达成效果和重要性给出自己的评价等级。

设定每个指标的效果和重要性都用表示5个等级符号来表示,即有序术语集为L={l0=FL(非常劣),l1=L(劣),l2=Y(一般),l3=H(好),l4=FH(非常好)}。专家用集合L中的一个或者相邻2个语言术语表达自己的评价结果。为了方便描述,作如下假设:Ei为第i个专家(i=1,2,…,r),Am为A维上第m个指标(m=1,2,3),Bn为B维上第n个指标(n=1,2,3,4),Cs为C维上的第s个指标(s=1,2,3,4,5),Zi为专家Ei的重要性等级(i=1,2,…,r),Oim为专家Ei给出的指标Am的重要性等级(i=1,2,…,r;m=1,2,3),Pin为专家Ei给出的指标Bn的重要性等级(i=1,2,…,r;n=1,2,3,4),Qis为专家Ei给出的指标Cs的重要性等级(i=1,2,…,r;s=1,2,3,4,5),Uim为专家Ei给出的指标Am的效果等级(i=1,2,…,r;m=1,2,3),Vin为专家Ei给出的指标Bn的效果等级(i=1,2,…,r;n=1,2,3,4),Wis为专家Ei给出的指标Cs的效果等级(i=1,2,…,r;s=1,2,3,4,5)[12]。

接下来是求得专家们对技术、经济和社会三方面的评价结果,具体步骤如下:

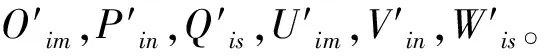
b. 由r个专家给出的语言评价可以得到指标重要性等级的平均值分别为

(1)

c. 将专家的重要性等级和专家对指标的效果等级集成为群评价信息:

(2)

d. 将式(1)所得指标的重要性等级和式(2)所得指标的结果等级集成维度，A，B，C的整体评价结果:

(3)

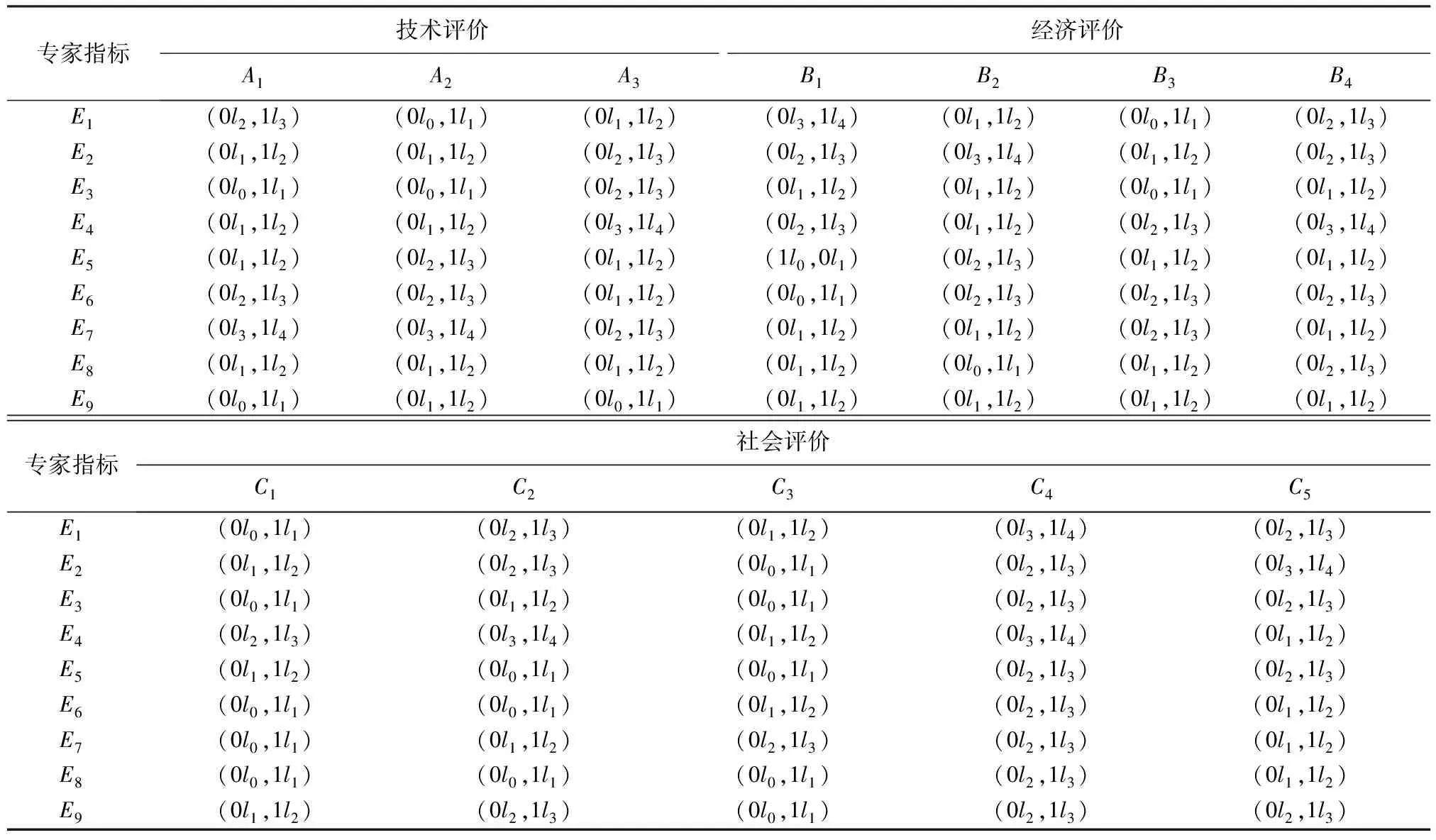
表1 指标效果评价的比例二元语义形式

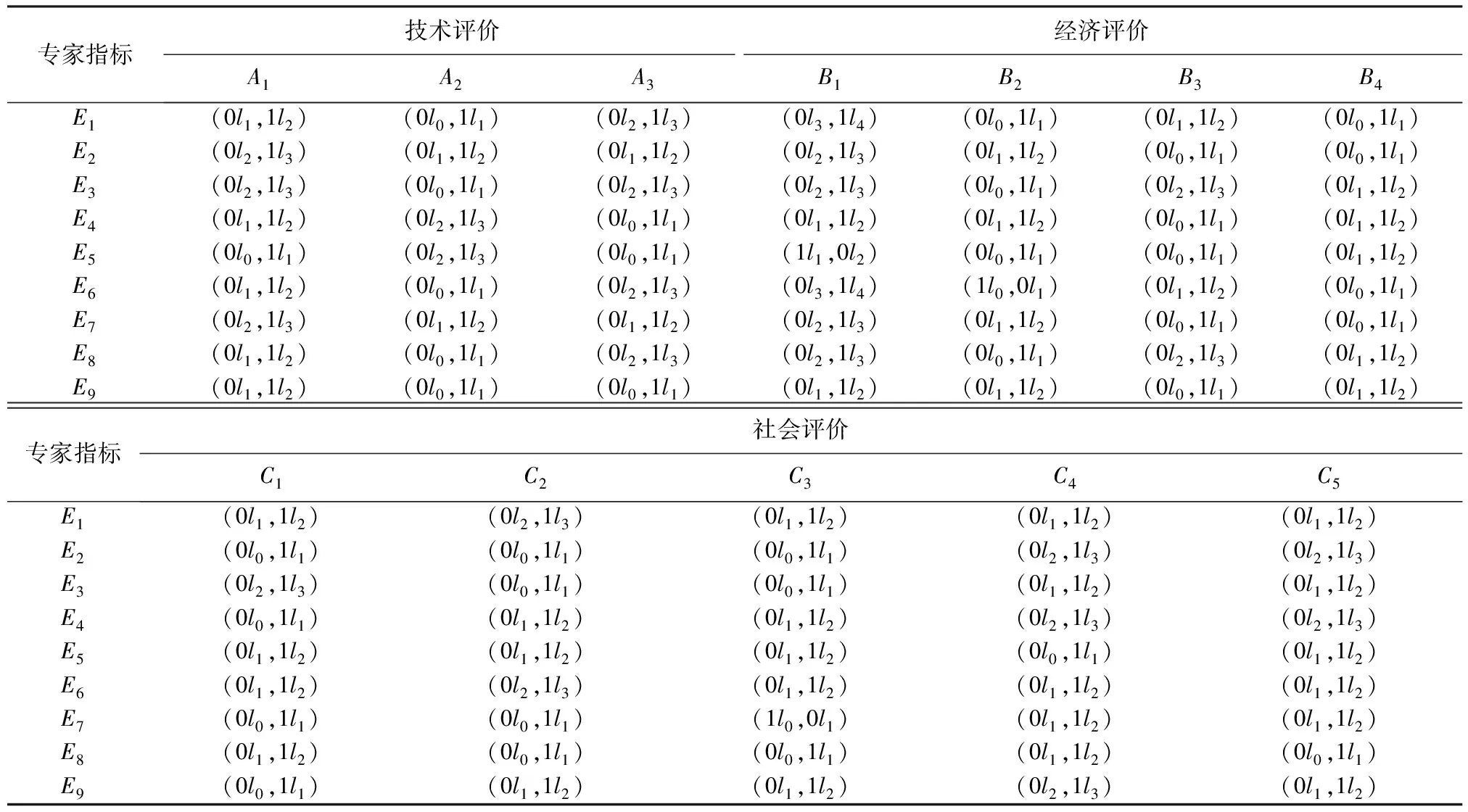
表2 指标重要性专家评价的二元语义形式

比例二元语义U，V，W分别为水利工程项目的技术评价、经济评价和社会评价结果,根据这3个维度的评价结合图2的判断矩阵模型可以判定水利项目的整体情况。

3 实例分析

某个水利工程项目在决定是否实施建设之前,首先要对其进行评价。现在在技术、经济、社会研究方面分别邀请了3位专家来评价水利项目。他们对各个指标效果和各个指标的重要性进行评价。根据上述定义将语言评价结果转化为比例二元语义的形式,见表1和表2。

假设各个专家的权重相同,根据上述理论部分的公式可以集成结果,见表3。

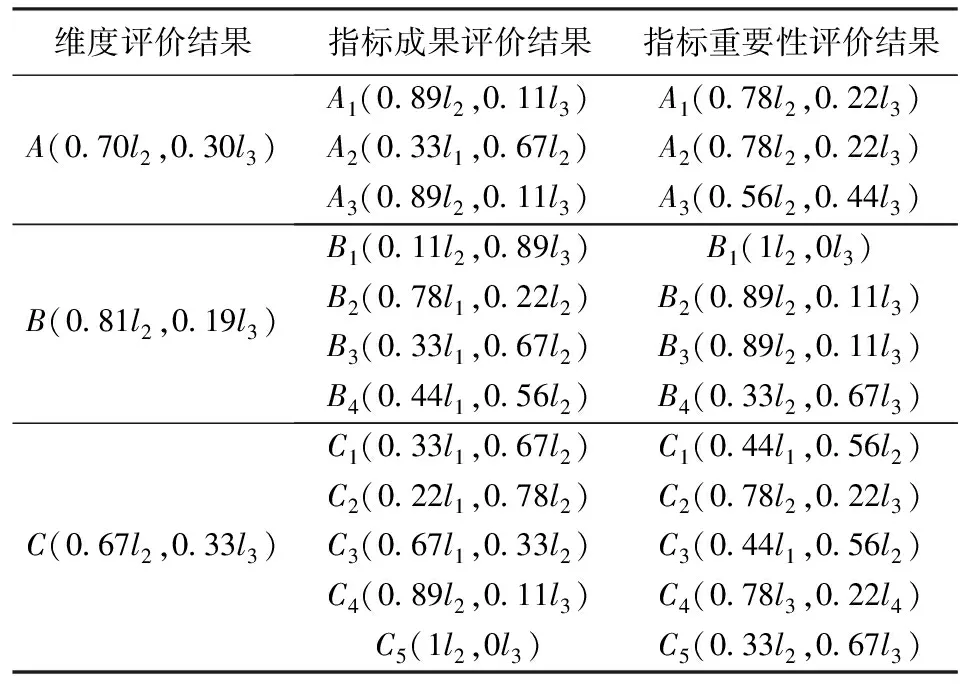
表3 水利工程项目的评价结果

由表3可知,这个水利工程项目的技术评价为 (0.70l2,0.30l3),经济评价为(0.81l2,0.19l3),社会评价为(0.67l2,0.33l3)。将这结果体现在图2的判断矩阵中,这个点应该落在Ⅳ区域中,所以这个水利项目整体是比较好的,其技术、经济和社会评价都是在一般评价以上,这样的项目是可以上马的。

4 结 语

一个水利项目的准确评价是决策项目是否实施的关键步骤。在现在对水利项目的评价方法存在明显不足的情况下,笔者基于比例二元语义提出一种新颖的评价方法,专家们根据预先设定的评价语言术语表达自己的观点,比例二元语义将语言术语量化为数值并集成最后的评价结果。此方法不仅可以方便评价定性的指标,而且可以提高评价的科学性和准确性。但是比例二元语义评价水利项目时也存在不成熟的地方,例如将可以准确量化的经济指标和量化困难的技术评价和社会评价指标同等对待,都纳入描述性语义一应俱全范围,可能反而降低评价结论的准确性。这就需要把比例二元语义改进或和其他方法相结合,提高水利项目评价的精准性。

参考文献：

[1] 杨义灿,郑垂勇,戴树声.模糊优选神经网络在水利投资项目评价中的应用[J].河海大学学报：自然科学版，2001,29(1):83-87.

[2] 刘铁刚,门宝辉.水利项目评价指标赋权模型的建立及其应用[J].东北水利水电,2003,21(7):1-3.

[3] 张慧,杨建斌.水利投资项目多目标模糊综合评价方法应用探析[J].长江科学院院报,2006,23(5):52-55.

[4] HERRERA F,HERRERA VIEDMA E.Linguistic decision analysis:steps for solving decision problems under linguistic information[J].Fuzzy Sets and Systems,2000, 115:67-82.

[5] WANG J H,HAO J.A new version of 2-tuple fuzzy linguistic representation model for computing with words[J].IEEE Transactions on Fuzzy Systems, 2006,14(3):435-445.

[6] 蒋水心,周之豪.水电建设项目的综合评价[M].南京:河海大学出版社,1995.

[7] 丰伟,吴泽宁.水运投资项目综合评价方法的研究[J].水运工程,1998(7):1-5.

[8] HERRERA F,HERRERA VIEDMA E.Choice processes for nonhomogeneous group decision making in linguistic setting[J].Fuzzy Sets and Systems,1998,94(3):287-308.

[9] ZADEH L A.The concept of a linguistic variable and its applications to approximate reasoning pt.Ⅰ[J].Information Science, 1975,8(3):199-249.

[10] ZADEH L A.The concept of a linguistic variable and its applications to approximate reasoning pt.Ⅱ[J].Information Science, 1975, 8(3):301-357.

[11] ZADEH L A.The concept of a linguistic variable and its applications to approximate reasoning pt.Ⅲ[J].Information Science, 1975,9(1):43-80.

[12] 王欣荣,樊治平.基于二元语义信息处理的一种语言群决策方法[J].管理科学学报,2003,6(5):1-5.