基于GI/G/1排队的人行横道宽度优化模型

，

(1.西南交通大学 交通运输与物流学院,四川 成都 610031;2.综合运输四川省重点实验室，四川 成都 610031；3.综合交通运输智能化国家地方联合工程实验室，四川 成都 610031)

0 引言

人行横道是行人穿越大多数交叉口的必经之路，考虑到行人的安全性、舒适性，人行横道的设计通行能力必须满足该人行横道的客流需求。交叉口人行横道的通行能力[1]受交叉口信号相位配置、人行横道宽度、长度以及行人特性的影响，其中，在其它条件一定的情况下，人行横道的宽度直接影响其设计通行能力。现有的《城市道路交通设施设计规范》(GB50688—2011)[2]中仅给出了人行横道宽度的参考值范围。然而在实际的人行横道宽度设计中，因很少考虑到行人服务水平[3]对其的影响，造成设计宽度很难满足高峰过街流量和行人安全的要求，所以目前的设计依据缺乏科学之城和实际指导意义。

因行人在人行横道入口处构成排队，因此可从排队论的角度来解决人行横道宽度设计问题。文献[4]中假设行人到达规律服从负二项分布，虽拟合效果较好却不利于排队建模的解析求解；文献[5]中是以行人到达规律为移位负指数分布为假设，虽然该分布便于建模却只适用描述无信号交叉口的行人到达规律。为此，考虑到指数分布[6]能够描述独立随机事件发生间隔且具有无后效性的特性，可假设行人到达规律服从该分布，并根据文献[7]中提出的行人服务率可以用正态分布描述的特点，结合信号交叉口行人过街具有周期性批量服务[8]的特性，综合考虑服务水平以建立到达时间间隔服从指数分布、服务时间间隔服从正态分布的GI/G/1排队模型来描述人行横道口排队现象，从而构建通行能力、服务水平与交叉口人行横道宽度取值的量化关联，实现人行横道宽度的合理设计。

1 人行横道排队系统描述和参数标定

1.1 人行横道排队系统描述

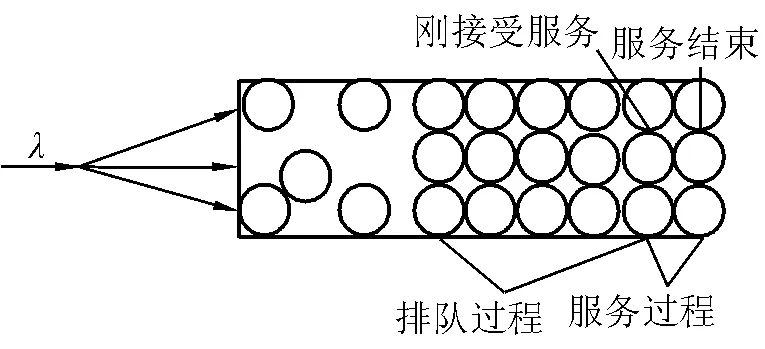
图1 人行横道入口处高峰时段排队系统

将人行横道与行人流描述成如图1所示的排队系统。假设沿人行横道宽度方向并列设有若干无形的服务窗口，每个窗口的宽度和长度都是确定服务等级下行人合理走行模式的安全区域直径[9-10]。为避免行人间相互侵犯彼此的安全区域而降低其服务水平，将窗口设置为正方形而不是矩形。

行人进入窗口视为在接受服务，离开窗口，视为服务结束。当行人之间处于合理模式[7]排队时，才认为按照规定服务等级进入了排队系统，而对于出在舒缓模式等级下的行人虽然进入了通道，因其行走为受到服务等级的影响而将其排除在排队系统之外，只有当他和排队的最后一名行人进入合理模式，才能纳入排队系统。

1.2 排队系统的参数标定

1.2.1 人行横道行人到达分布

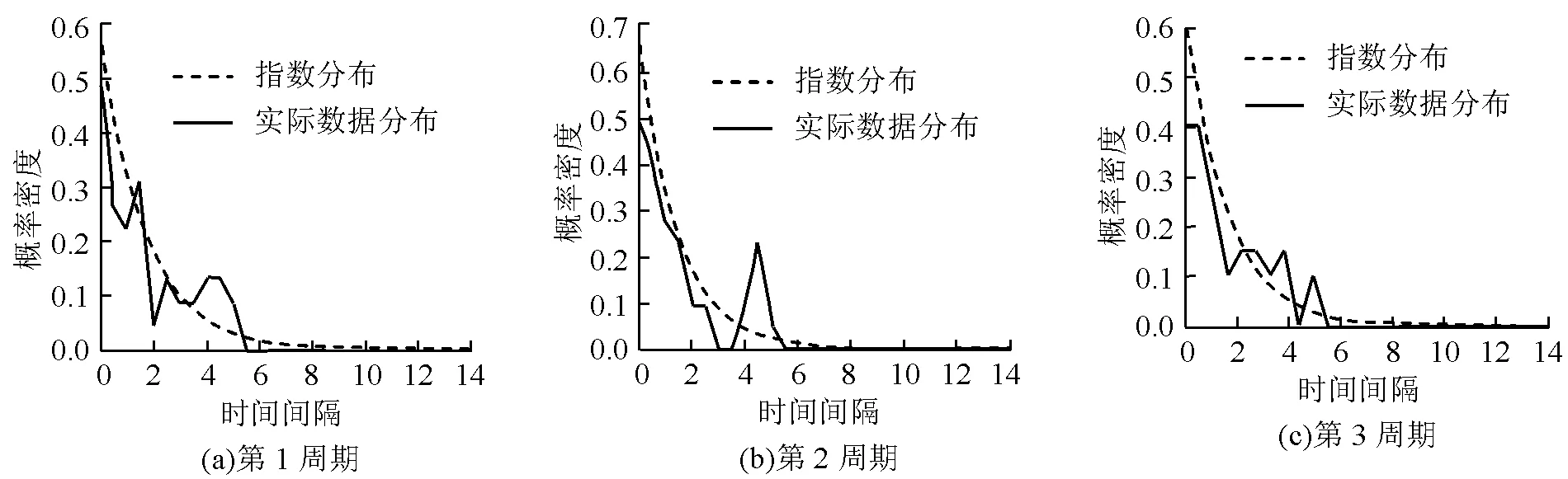
由第1节中提到本文以行人到达信号交叉口人行横道的时间间隔服从指数分布为假设，为验证该假设成立，选取成都市八宝街—宁夏街信号交叉口作为数据采集地点，以高峰时期西大街行人到达人行横道的视频作为数据来源基础，因本文研究的是行人到达人行横道的到达时间间隔，故将每个周期所调查的行人到达时间间隔作为一组数据。经实地调查，通过对获得的数据利用SPSS软件对数据进行游程检验以验证数据的有效性，取置信区间为95%，最终共获得西大街15组有效数据备用，如表1为该街道数据的统计显著性。通过对行人到达时间间隔的有效数据进行分布拟合，可由MATLAB编程得到其数据分布拟合图如图2所示，具体的每一周期的拟合度由表2所示。

表1 西大街人行横道行人到达时间间隔游程检验的统计显著性

表2 西大街行人到达规律服从指数分布的拟合度

从表1中可以看出，每组数据的显著性均大于显著性水平0.05，说明调查数据均为随机序列，可进行统计分布的拟合。而从表2和图2可以看到，以行人到达人行横道的时间间隔数据服从指数分布的平均拟合度为81.67%，拟合度较高，说明指数分布拟合行人到达规律与实际情况较符。因此，该假设成立，可以指数分布描述行人到达人行横道的到达规律。单位时间内行人到达分布A(x)可描述如下

A(x)=1-e-λx

(1)

1.2.2 行人服务时间的分布

由参考文献[7]和文献[11]可知，步行速度v服从正态分布，调查八宝街附近得到实验验证，使用w测试方法得到的步行速度显着水平α为0.05遵循正常的分布。因此，根据目标服务水平的步行速度分布遵循正态分布N(μ，δ2)，μ为平均速度，δ2为标准差。同样根据文献[7]可知，安全区域面积是以人的自身为圆心形成的圆，在选定服务等级情况下可确定人均安全面积S，其直径为

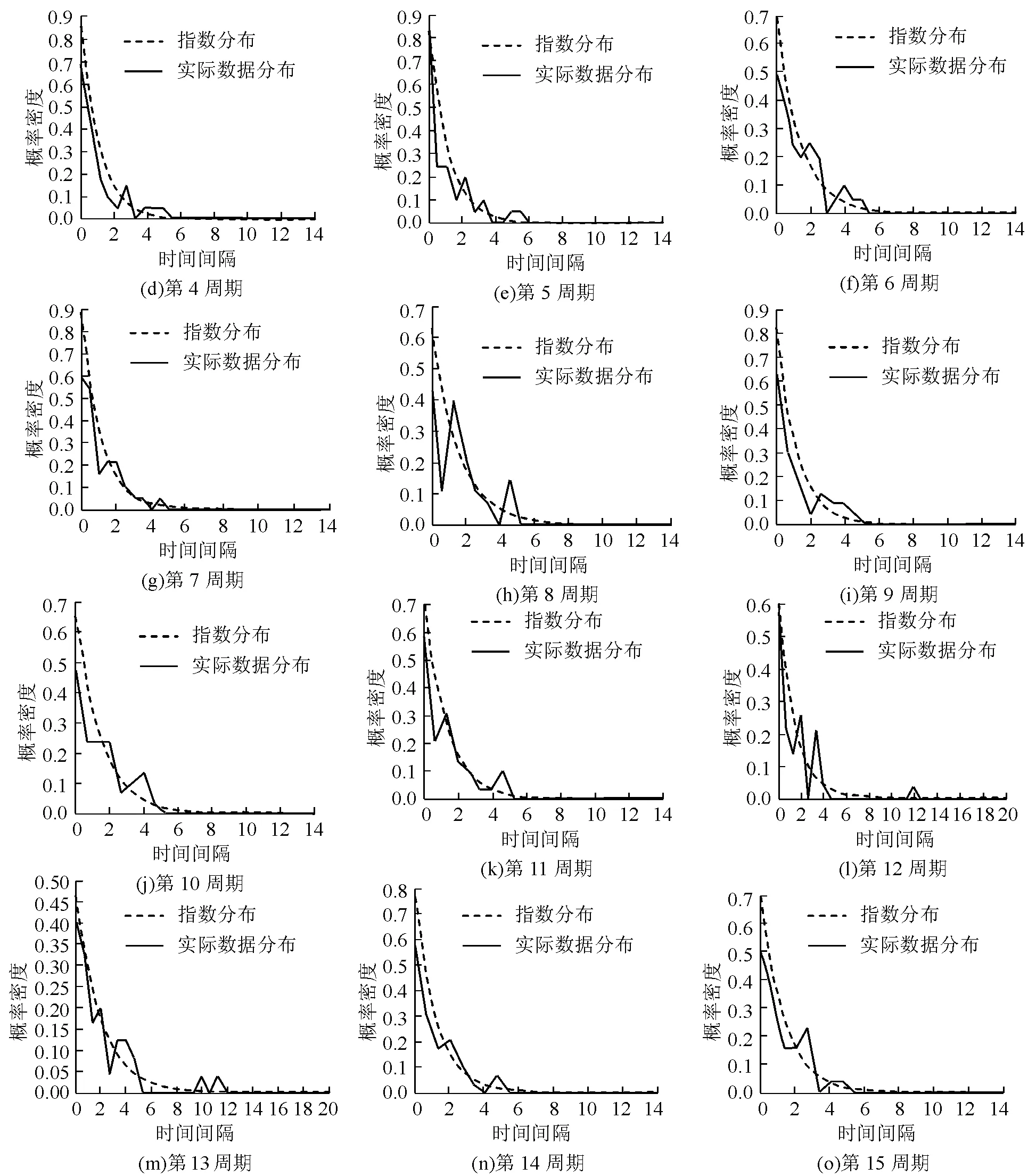
图2 西大街行人到达时间间隔基于指数分布拟合效果图

(2)

式中,d为2.1节中定义的正方形服务窗口边长。

由人行横道排队系统描述可知，旅客被服务的本质是通过正方形窗口的过程，从而服务时间等于窗口边长d除以旅客速度v，因此，服务时间随机变量R的分布B(x)[7]可以表示为

(3)

因此，服务时间随机变量R的均值E(R)和方差D(R)可表达为

(4)

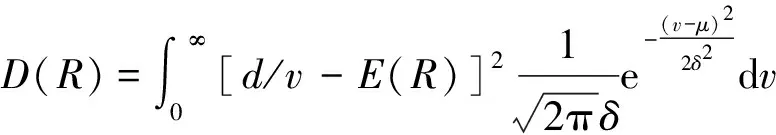
(5)

2 排队优化模型的建立

2.1 问题分析

在高峰时段，行人在人行横道入口处形成排队，行人之间除了安全距离，没有其它空间，无法插队，因此，用c个到达时间间隔服从指数分布、服务时间间隔服从正态分布的GI/G/1模型来描述如图1所示的排队系统。因信号交叉口人行横道因信号周期中的红绿灯具有忙期、闲期特性，且该排队模型对于忙期和闲期均有成熟的解析解，因此，通过限制某些指标可以达到优化排队系统的目的。

2.2 模型建立

(1)确定目标函数。因人行横道宽度等于服务窗口数乘以其边长d，d为常数，因此要设计能够满足一定约束的最小人行横道宽度等价于设计最少的窗口数。

(2)给定约束条件。对于该排队系统，必须满足其服务强度ρ小于1，否则将是无限排队的情形。这里的服务强度指平均服务时间除以平均到达时间，因此可表示为

(6)

因信号交叉口行人通过人行横道需要受到交叉口信号控制，行人只能在人行信号灯为绿灯时通过人行横道，红灯则禁行。对于每个用GI/G/1模型描述的窗口，考虑到排队系统具有忙期和闲期，可视人行信号绿灯时段为排队系统的忙期m，红灯时段为排队系统的闲期e。对于该排队系统，忙期服务的客流应与绿灯时段通过人行横道的客流相等。为保证人行道、机动车道和人行横道的相互独立性，应在人行横道入口处设置合理的等候区，可设等候区的长度为l，等候区可容纳的行人数量则为Cl。为了避免行人的二次过街，等待区域的等待人数Cl必须小于或等于忙期的排队系统中的服务的数量EM，该约束表示如下：

(7)

综合考虑到行人的服务水平，则设计的行人人均安全面积需小于或等于设计的服务等级下的人均安全面积。因行人在人行横道前设有等候区域，设有等候区的长度为l，确定的等候面积为M，则设计行人人均安全面积S为M/(Cl)，而每一设计服务水平均有其相对应的人均安全面积S设计，则该基于服务水平考虑的约束条件可表示为

M/(Cl)≤S设计

(8)

为满足给定等级下的服务水平，窗口数至少为1，窗口约束表达为

C≥1

(9)

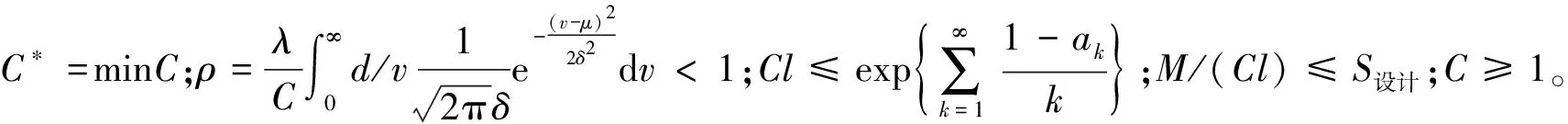
3 结束语

由以上分析可知，行人到达人行横道的时间间隔服从指数分布，行人服务时间服从正态分布。从排队论的角度出发，考虑行人在人行横道的批量通过特性，综合考虑到行人服务水平对行人的安全舒适性的影响，建立了人行横道入口处行人的GI/G/1排队模型，给出了基于该模型并结合信号交叉口的信号特点提出的几个重要约束，优化人行横道宽度的计算模型，为人行横道的宽度取值提供了计算依据。

参 考 文 献

[1]冯绍海，李淑庆，谢晓忠.交叉口人行横道通行能力研究[J].交通信息与安全，2011，29(1)：20-24.

[2]上海市城乡建设和交通委员会. GB50688—2011 城市道路交通设施设计规范[S]. 北京：中国计划出版社，2011.

[3]钱大琳，张敏敏，赵伟涛. 行人服务水平评价的半定量方法[J].华南理工大学学报:自然科学版，2012，40(7)：33-40.

[4]董良海.城市信号交叉口人行横道处行人通行能力研究[D].北京:北京工业大学，2008.

[5] 夏晶. 基于效率和安全的人行横道合理间距研究[D].武汉:武汉理工大学，2008.

[6] 祝东进，郭大伟，刘晓. 概率论与数理统计[M]. 北京：国防工业出版社，2010.

[7] 蒋阳升,胡路,卢果.基于排队论的地铁人性通道宽度取值方法[J].交通运输工程学报，2010，10(3)：67-71.

[8] 李民. 马尔可夫骨架过程与GI/G/1排队系统[D].长沙:中南大学，2003.

[9] 谭方彤. 商店营业厅顾客人均使用面积计算方法的研究[J] .华中建筑， 2006, 24( 10)：100-101.

[10] 全国人类工效学标准化技术委员会.GB/ T 10000—1988 中国成年人人体尺寸[S] . 北京：中国标准出版社，1988.

[11] 龚晓岚, 魏中华. 行人交通流自由速度模型研究[J].北京工业大学学报，2009, 35( 4)：493-497.