一种低压分段线性曲率校正CMOS带隙基准源设计
2014-03-22胡利志
陈 涛,胡利志,乔 明
(电子科技大学电子薄膜与集成器件国家重点实验室,成都 610054)
一种低压分段线性曲率校正CMOS带隙基准源设计
陈 涛,胡利志,乔 明
(电子科技大学电子薄膜与集成器件国家重点实验室,成都 610054)
在传统低压带隙基准的基础上,通过设计与热力学温度成正比的电流(IPTAT)及与热力学温度呈互补关系的电流(ICTAT),实现节点电流相减,从而产生分段线性电流作为基准源的曲率校正分量,设计了一个性能更佳的曲率校正带隙基准。电路采用低压运放及低压PTAT电流产生模块,工作电压低。Cadence仿真结果显示,在-40~125 ℃温度范围内,平均温度系数大约3×10-6℃-1,最低工作电压在1 V左右,可用于低电源电压、高精度的集成芯片。
带隙基准;曲率校正;温度系数
1 引言
基准源在各种电路系统中均扮演着重要的角色,为其他子电路提供稳定的工作点,它的输出信号不随电源电压、温度和瞬态负载的变化而有显著的波动[1]。在众多的基准源中,带隙基准源因其高精度、低噪声、高电源抑制比、低工作电压等优点而受到人们的青睐。
随着片上系统(SOC)的不断发展与电路集成度的不断提高,以及电池供电便携式设备的不断涌现,传统的带隙基准无论是从工作电压还是精度上都越来越难满足日益复杂的系统需求。针对以上问题,本文设计了一款具有低电源电压、高精度的带隙基准源。基于CMOS工艺,在传统低压带隙基准的基础上,采用低压运算放大器,应用MOS管的亚阈值特性及三极管VBE的负温度特性引入分段线性电流,实现了带隙基准的曲率校正,得到工作电压低至1 V、温度系数低于3×10-6℃-1的CMOS带隙基准源。
2 带隙基准原理与低压带隙基准
2.1 带隙基准原理
带隙基准设计的第一步是找到已被良好表征且几乎不随工艺波动而改变的电压或电流值。传统的带隙基准利用pn结二极管正向电压(双极型晶体管的VBE)和工作在不同电流密度下的双极晶体管基极-发射极电压的差值ΔVBE实现。VBE具有负温度系数,ΔVBE具有正温度系数,将这两个具有相反温度系数的电压按一定的权重相加,就得到一个零温度系数的电压[2],即:
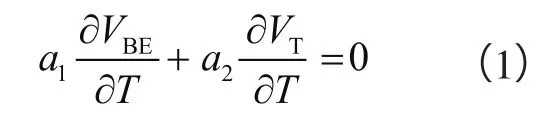
此时有:
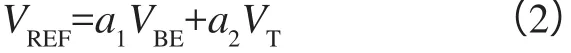
传统带隙基准由于VBE自身大小及正、负温度系数相差较大等因素的限制,相加后得到的基准电压在1.21 V左右,很难实现低电压的基准值。同时由于VBE的温度特性非线性,由式(2)得到的基准电压的温度特性曲线如图1所示,通常为一条上凸的曲线,被称作一阶带隙基准源。

图1 一阶带隙基准的温度特性
2.2 传统低压带隙基准
图2是BanBa等人提出的低压CMOS带隙基准源[3],图中的二极管为基极-集电极短接的PNP三极管。M1~M3具有相同的宽长比,因此有I1=I2=I3,运放钳位作用使得X、Y点电压相等,电阻R1、R2具有相同阻值,因而流过电阻R1与R2的电流相等,即I1a=I2a,且I1a=VBE/R。又因为I1b=I2b,而I2b=ΔVBE/R3=VTlnn/R3,其中n为三极管的发射极面积比。综上所述可得:
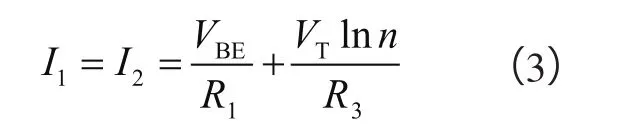
合理设置R1、R3与n的值,可以得到零温度系数的电流,通过M3的镜像作用有:
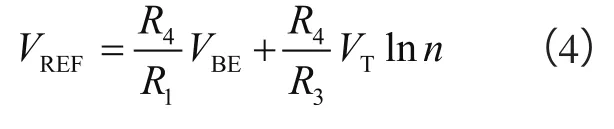
得到的VREF为一阶线性补偿的基准电压。
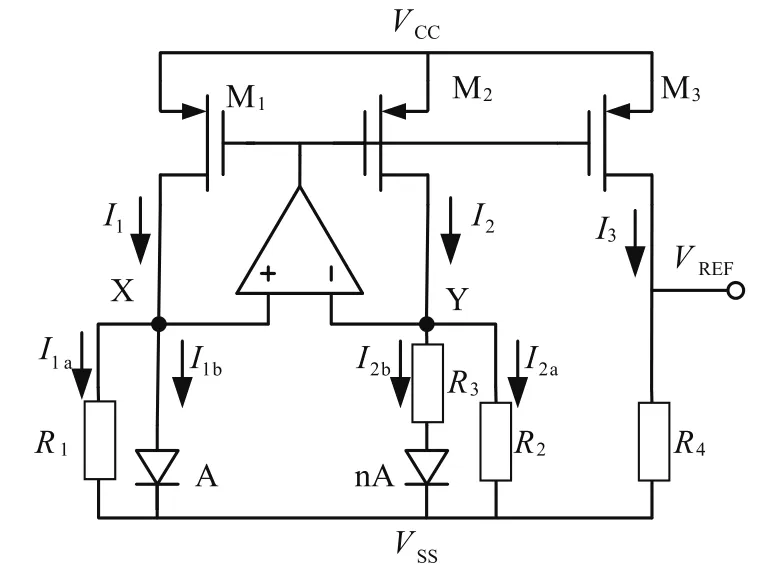
图2 传统低压CMOS带隙基准
3 曲率校正CMOS带隙基准源
3.1 基极-发射极电压的温度特性
双极型晶体管的基极发射极电压VBE在大量的文献中得到详细的推导,其中一个较常用的表达式为[4,5]:
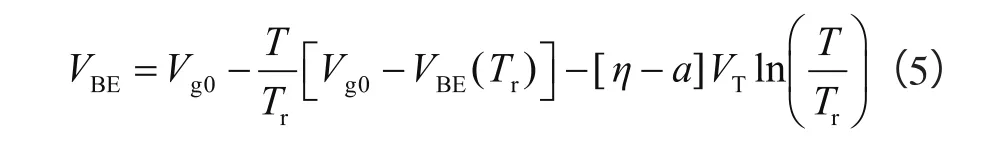
式中,Vg0表示二极管电压在绝对0度时的值;T表示热力学温度;Tr表示某一基准温度;[η-a]为与工艺相关的常数。将上式中的对数部分进行泰勒级数展开并整理,可得到VBE的表达式为:
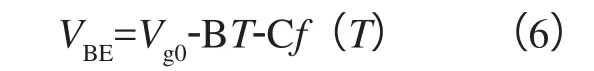
其中B和C是与温度无关的常数;f(T)代表温度T的所有高阶分量。
一阶带隙基准抵消了电压的线性温度分量,曲率校正带隙基准的目的是补偿带隙基准的非线性分量。实现曲率校正的方法有很多种,其中包括PTAT2曲率校正技术[6]、与温度相关电阻比例技术[7]、二极管环路技术[8]、精确抵消技术[9]和分段线性补偿技术[10]等。
3.2 分段线性曲率校正理论
本文中使用的分段线性曲率校正方法基于文献[10]中Rincon-Mora提出的理论,如图3左所示,M1为非理想电流源,流过的电流温度特性与热力学温度呈互补关系。在温度范围的低温段,ICTAT>IPTAT,流过电流源的电流由M1足以提供,因此M2关断;而在温度范围的高温段,ICTAT<IPTAT,强制M2开启并提供这两个电流的差值,通过M3的镜像作用,可得到INL的值为:
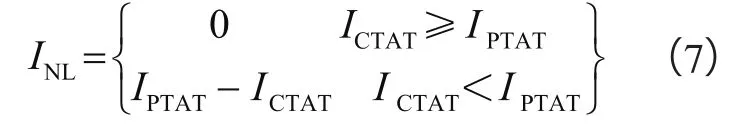
式中K1、K2为常数。
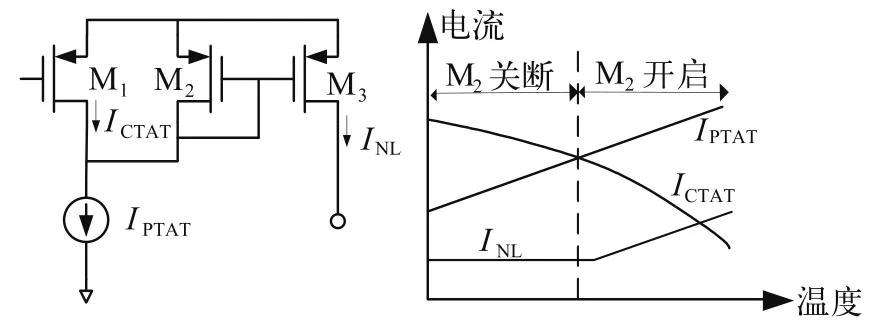
图3 分段线性曲率校正技术
3.3 分段线性曲率校正电路
本文中设计的分段曲率校正电路如图4所示,M1~M4和R1构成低电源电压IPTAT产生电路,M1、M2工作在亚阈值区,具有三极管VBE相似的温度系数,R1上的电压为M1与M2栅源电压的差值,类似于ΔVBE,具有与热力学温度成正比的温度特性,流过R1电流为:
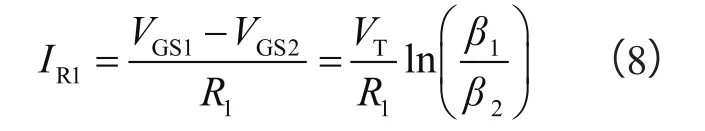
其中β1、β2分别表示M1与M2跨导因子和宽长比的乘积。从式(6)中可以看出,IR1的大小由β1、β2以及R1的阻值共同决定,而其温度特性与VT一致,即与热力学温度成正比。
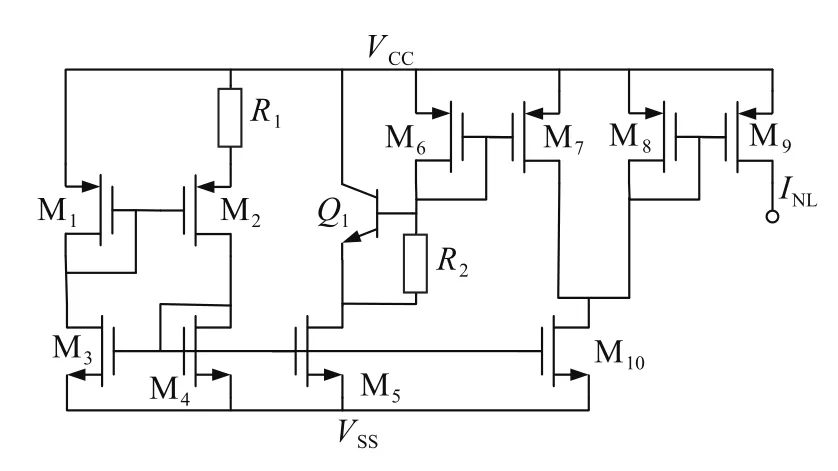
图4 分段线性曲率校正电路
图4中剩余部分是图3左的具体电路实现,M5镜像PTAT电流,R2上流过的电流为:

其中VBE为三极管Q1的基极-发射极电压,忽略三极管Q1的基极电流,流过晶体管M6的电流具有负的温度特性,即ICTAT。在设计时应满足在整个温度范围内IM5>IR2,以保证Q1工作在正向偏置区。M10中流过的电流为IPTAT,M7镜像M6的电流并与M10中的电流进行比较,当IM7>IM10时,M7工作在线性区并且满足IM7=IM10,此时M8处于截止状态。而随着温度的升高,M7的电流逐渐减小而M10电流逐渐增大,当IM7 其中S8、S9分别表示晶体管M8与M9的宽长比。 3.4 整体电路 本文中设计的带隙基准整体电路结构如图5所示,电路的前半部分是前文分析的分段线性曲率校正电路,后半部分为传统的一阶低压带隙基准,最后得到的基准电压为VREF。为了保证整体电路能够工作在较低电源电压下,一阶带隙基准中的运放使用了低压运算放大器,运放电路如图6所示,它只需要电源电压大于晶体管的阈值电压即可正常工作[11]。本文中带隙基准的基准电压值为: 图5 整体电路 图6 低压运放 分段线性曲率校正电流的仿真结果如图7所示,图中分别显示了ICATA、IPTAT和INL的波形,与前文分析一致,当温度小于50 ℃时,ICATA>IPTAT,此时INL=0,而当温度大于50 ℃时,ICATA 输出电压VREF随温度变化的仿真结果曲线如图8所示,仿真时电源电压VCC为1.8 V,温度范围为-40~125 ℃,从图中可以看到,当温度小于50 ℃时,由于INL并未起作用,温度特性曲线与一阶带隙基准温度特性一致,随着高温段分段线性曲率校正电流的引入,VBE的非线性分量得到了补偿。在整个温度范围内,基准电压的平均温度系数低于3×10-6℃-1。 图7 分段线性曲率校正电流 图8 VREF温度特性 图9是电路的工作电压仿真图,从图中可以看到,电路在0.8 V即可正常工作,工作电压大于1 V时,基准电压值稳定在594 mV。 图9 工作电压仿真图 在传统低压带隙基准的基础上,本文通过引入分段线性曲率校正电流分量对一阶带隙基准进行补偿,获得了精度高、工作电压低的曲率校正带隙基准。Cadence中仿真结果显示:1.8 V工作电压下,-40~125 ℃温度范围内基准电压的温度系数小于3×10-6℃-1。电路使用了低压IPTAT产生电路以及低压运放,因此整体电路的工作电压很低,DC分析显示电路的最低工作电压约1 V。适用于工作电压低、基准电压精度要求高的集成电路芯片。 [1] Gabriel A R. Voltage references from diodes to precision high-order bandgap circuits [M]. 北京:科学出版社, 2013. 1-5. [2] Behzad Razavi. 模拟CMOS集成电路设计[M]. 西安:西安交通大学出版社, 2002. 314-319. [3] BANBA H, SHIGA H, UMEZAWA A, et al. A CMOS bandgap reference circuit with sub-1-v operation [J]. Journal of Solid State Circuits, 1999, 34(5): 670-674. [4] TSIVIDIS Y P. Accurate analysis of temperature effects in Ic-Vbe characteristics with application to bandgap reference sources [J]. Journal of Solid State Circuits, 1980, 15(6): 1076-1084. [5] MEIJER G M. A new curvature-corrected bandgap reference [J]. Journal of Solid State Circuits, 1982, 17(6): 1139-1143. [6] Gray P. advanced analog integrated circuits [Z]. Lecture notes and diagrams from the University of California at Berkeley. [7] Leung C Y, Leung K N, Mok K T. Design of a 1.5 V high order curvature-compensated CMOS bandgap reference [J]. Circuits and Systems, 2004, 1: 48-52. [8] Gunawan M. A curvature-corrected low-voltage bandgap reference [J]. Journal of Solid State Circuits, 1993, 28(6): 667-670. [9] Meijer G M. A new curvature-corrected bandgap reference [J]. Journal of Solid State Circuits, 1982, SC-17(6): 1139-1143. [10] Rincon Mora G A, Allen P E. A 1.1 V current-mode and piecewise-linear curvature-corrected bandgap reference [J]. Journal of Solid State Circuits, 1998, 33(10): 1551-1554. [11] Allen P E, Holberg D R. CMOS模拟集成电路设计[M].北京:电子工业出版社, 2005. 348-351. Design of a Low Supply Piecewise Curvature Corrected CMOS Bandgap Reference CHEN Tao, HU Lizhi, QIAO Ming (State Key Laboratory of Electronic Thin Films and Integrated Device,University of Electronic Science and Technology of China,Chengdu610054,China) Based on the traditional low supply voltage bandgap reference, by designing current proportional to absolute temperature(IPTAT)and current complementary to absolute temperature(ICTAT)which are subtracted from one another, a piecewise linear current is achieved and used as the curvature correction component. Thus, a better performance curvature corrected bandgap reference is proposed. The circuits use low-voltage amplif i er and low-voltage IPTAT generator, so the operation voltage is low. Simulation results with Cadence indicate that the bandgap reference has an average temperature coeff i cient of 3×10-6℃-1within a temperature range between -40~125 ℃centigrade, and the power supply is as low as 1 V, the circuits can be used in low power supply and high-precision SOCs. bandgap reference; curvature correction; temperature coeff i cient TN432 A 1681-1070(2014)09-0036-04 陈 涛(1988—),男,四川南充人,硕士研究生,主要研究方向为模拟集成电路设计。 2014-05-08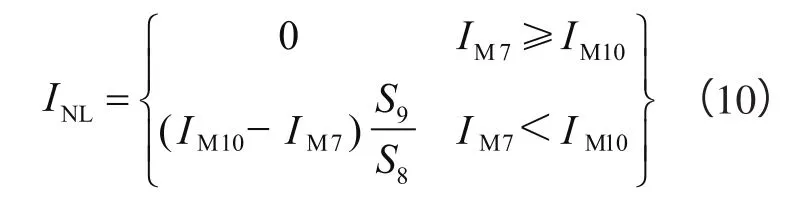
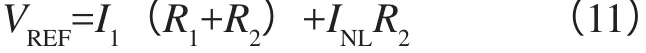

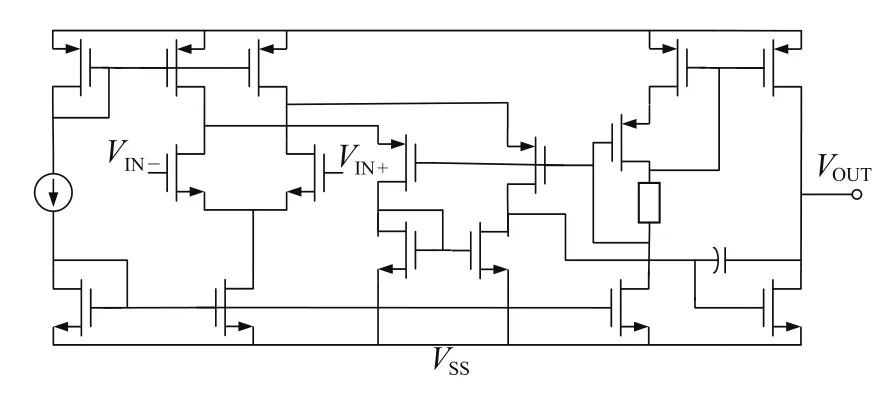
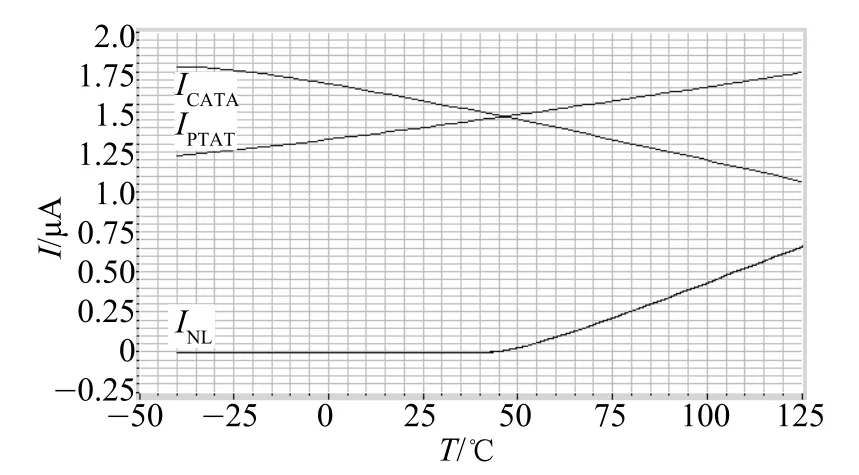
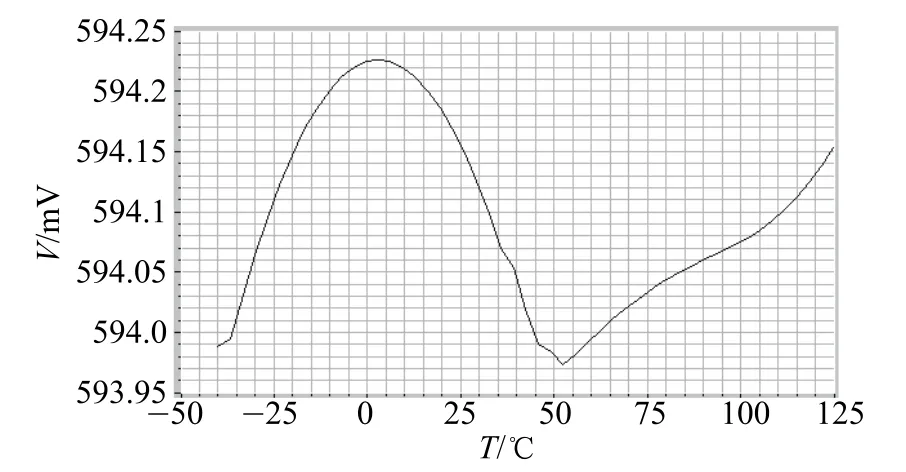
4 仿真与分析
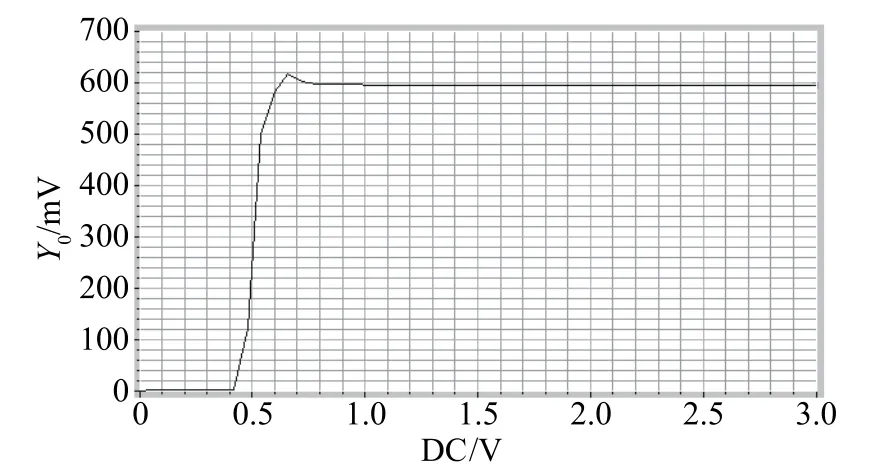
5 结束语

