基于调制随机共振的微弱信号频率检测方法

李忠虎，蔡志全

(内蒙古科技大学信息工程学院，内蒙古包头　014010)

0　引言

从工业现场采集到的信号被强噪声淹没，信号相对于噪声显得极其微弱，信噪比很低[1]。传统的信号处理方法主要是通过滤波等方法去除和抑制噪声，进而实现对微弱信号的检测，但是在去噪的过程中，信号本身受到了损失。

通过随机共振的概念可知，随机共振是利用噪声而非抑制噪声。随机共振的绝热近似理论与线性响应理论对研究对象有着很强的限制条件，只有在低频、小信号时利用随机共振检测才有很明显的优势[2]。实际检测的微弱信号频率不可能远远小于1 Hz，一般在几十甚至数百Hz，因此在较高频率下实现微弱信号检测成为随机共振研究的一个关键。

1　双稳态系统的随机共振

随机共振模型一般包括3个基本要素：微弱的输入信号、噪声、用于信号处理的非线性系统。双稳态系统的随机共振模型如图1所示。

图1　双稳随机共振模型

随机共振的双稳态系统由Langevin方程描述：

(1)

f(x)=ax-bx3

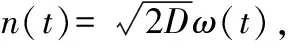
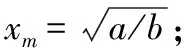
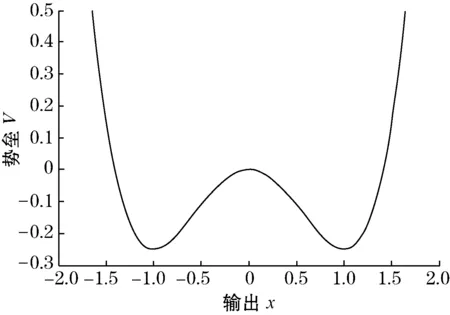
图2　双势阱示意图

根据绝热近似理论及线性相应理论，在小的外力作用下输出信噪比为

(2)

由式(2)可知，在a，b，A固定的情况下，随着噪声强度D的增大输出信噪比呈现一个先增大后减小的过程，在D=ΔV/2时取得最大的信噪比，也就是说这时随机共振最明显[3]。

2　调制随机共振

绝热近似法以及其近似理论研究表明：随机共振的应用在小参数的条件下才有明显优势，这样限制了其在工程中的应用[4]。对于信号频率远大于1 Hz的情况下，可以采用对信号进行调制、采样频率压缩、时序步进采样、调节系统参数等方法，相对于其他方法，采用调制后的方法比较简单，系统的工作量比较低，也便于实现。

调制随机共振的基本思想是将被测信号用载波信号进行调制[5]，调制后的信号引入到双稳随机共振系统中。调制后的低频信号满足小参数的随机共振条件要求，可以产生随机共振。最后对随机共振系统的输出信号进行解调处理，这样就得到了被测信号。调制随机共振系统的结构如3所示。

图3　调制随机共振系统结构图

设待测信号S(t)=Acos(2πf0t)，噪声为n(t)，频率可变的载波信号V1(t)=cos(2πfct)。

经过调制后进入随机共振系统的信号为

X(t)=[S(t)+n(t)]·V1(t)

=S(t)×V1(t)+n(t)·V1(t)

(3)

=Acos(2πf0t)cos(2πfct)+n(t)cos(2πfct)

因为高斯白噪声经过调制后还是白噪声，这样，进入随机共振系统的信号为

(4)

由式(4)可知，经过调制后得到了2个不同频率的信号，当调节载波信号接近待测信号频率时，差频信号相当于绝热条件下的小频率信号，进而产生随机共振。因为和频信号的频率远远大于1 Hz，不满足绝热条件下的小频率信号检测的要求，所以不会对系统产生影响。

3　调制随机共振仿真分析

通过Matlab平台进行基于随机共振的微弱信号检测仿真实验，采用工程上应用广泛的四阶龙格-库塔法[6]进行求解。

k1=f(xi，yi)

k2=f(xi+h/2，yi+h·k1/2)

k3=f(xi+h/2，yi+h·k2/2)

k4=f(xi+h，yi+h·k3)

yi+1=yi+h·(k1+2k2+2k3+k4)/6

(5)

输入周期信号为

x(t)=S(t)+n(t)=Acos(2πft+φ)+n(t)

(6)

在系统中加入幅值为0.2 V，频率为50 Hz的余弦信号；强度为5 V的限带高斯白噪声；系统参数取值为a=1，b=1。设置采样频率为2 000 Hz，调节信号发生器的频率，观察输出信号的幅频特性曲线，当信号发生器频率为49.9 Hz时系统输出波形如图4、图5所示。

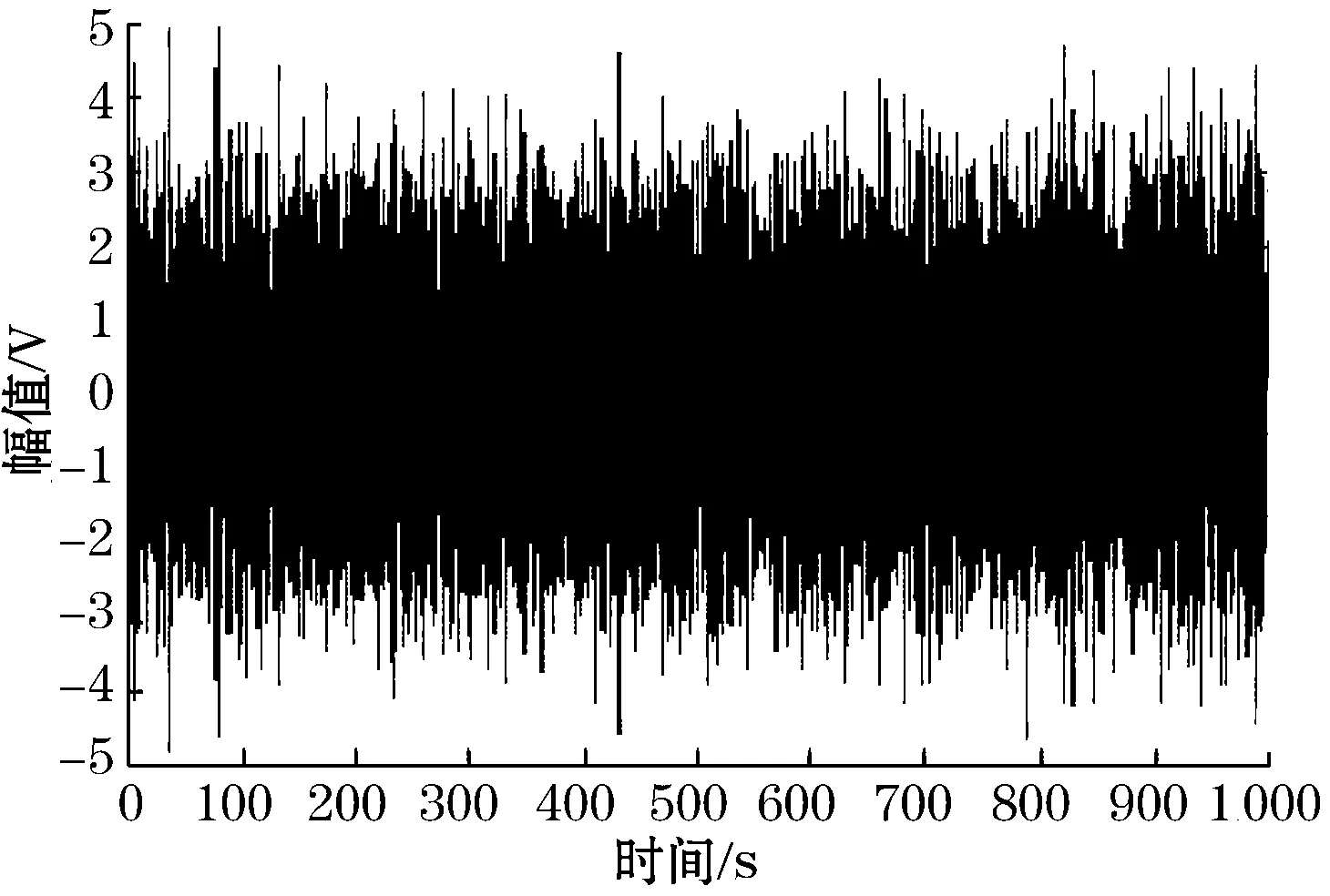
(a)输入信号波形

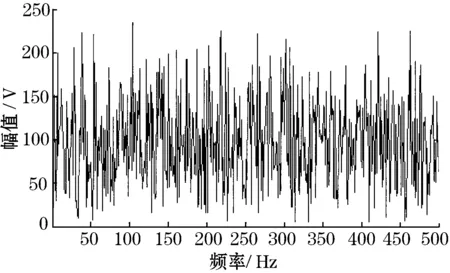
(b)输入信号的频谱

图4(a)、图4(b)分别是被强噪声淹没的信号的时域和频域波形图，观察分析图4(a)、图4(b)可知，信号已经被强噪声信号所淹没，得不到有关信号的任何信息。

将被噪声污染的信号输入到调制随即共振系统后，系统输出为图5(a)、图5(b)。

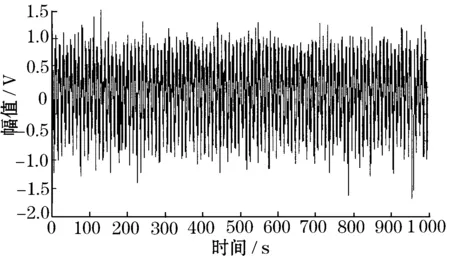
(a)调制随机共振输出波形

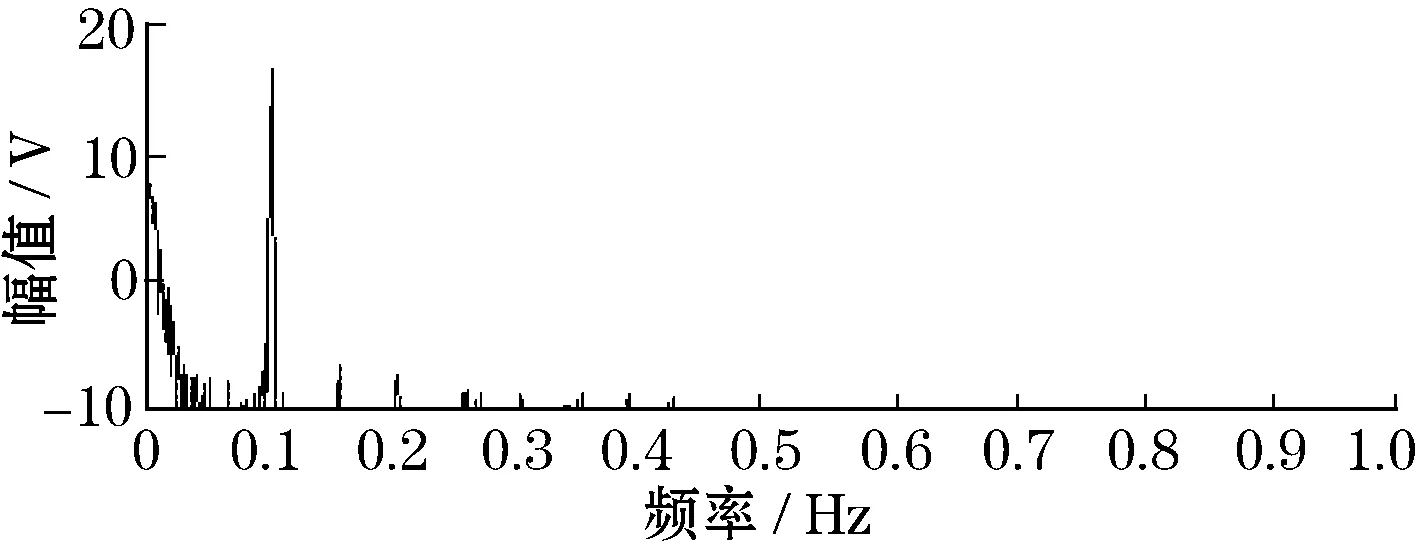
(b)调制随机共振输出频谱

观察经过调制随机共振系统后输出信号的频谱可知，调制信号的差频分量被检测出来，也就是说微弱特征信号的频率被检测出来。

4　调制随机共振电路设计

调制随机共振硬件电路如图6所示。调制随机共振电路中采用模拟乘法器AD633，它是一款完整的四象限乘法器，单芯片结构和激光校准使这款器件稳定可靠，同时乘法器精度基本上对电源不敏感。通过调制电路实现了待测信号和载波信号相乘，使得输出含有和频以及差频信号。差频信号相当于绝热条件下的小频率信号，进而产生随机共振，而和频信号不会对系统产生影响。

图6　调制随机共振硬件电路图

AD633作为随机共振电路的乘法器，LM324作为电路的积分器。积分器U2A的输出信号为-x，经过U2B的反向放大作用信号为K0x；经过乘法器U4之后得到输出信号为K1x2，乘法器U3的输出为-K2x3。RV1、RV2为参数可调的滑动电阻，用来调节分压系数，从而能够容易地实现信号强弱的调整，更容易实现随机共振。

5　结束语

文中研究了基于调制随机共振的微弱信号频率检测方法。对调制随机共振方法进行了仿真研究，仿真效果良好。根据调制随机共振仿真实验设计了硬件电路，为随机共振应用于工程实际提供了实现方案。

参考文献：

[1]高晋占．微弱信号检测．北京：清华大学出版社，2012．

[2]HE Q B，WANG J．Effects of multiscale noise tuning on stochastic resonance for weak signal detection．Digital Signal Processing，2012，22(4)：614-621．

[3]LENG Y G，WANG T Y．Engineering signal processing based on bistable stochastic resonance．Mechanical Systems and Signal Processing，2007，21(1)：138-150．

[4]胡茑庆．随机共振微弱特征信号检测理论与方法．北京：国防工业出版社，2012．

[5]张丽珠，于键．基于调制随机共振大频率信号检测的仿真．天津职业技术师范大学学报，2012，22(4)：45-47．

[6]李丹．四阶龙格-库塔法在火控解算中的应用．微计算机信息，2011，27(3)：192-193．

[7]杨定新，胡茑庆．基于随机共振电路模拟的微弱周期信号检测．电路与系统学报，2004，9(6)：135-138．